机器学习进阶之(六)CatBoost
1.CatBoost简介
俄罗斯人提出了CatBoost,这个算法在其论文中与GBDTS算法对比,注意,这里的GBDT算法不是简单的GBDT算法,而是作者将GBDT与XGBoost统称为GBDTS。这两个算法具体的差别是:
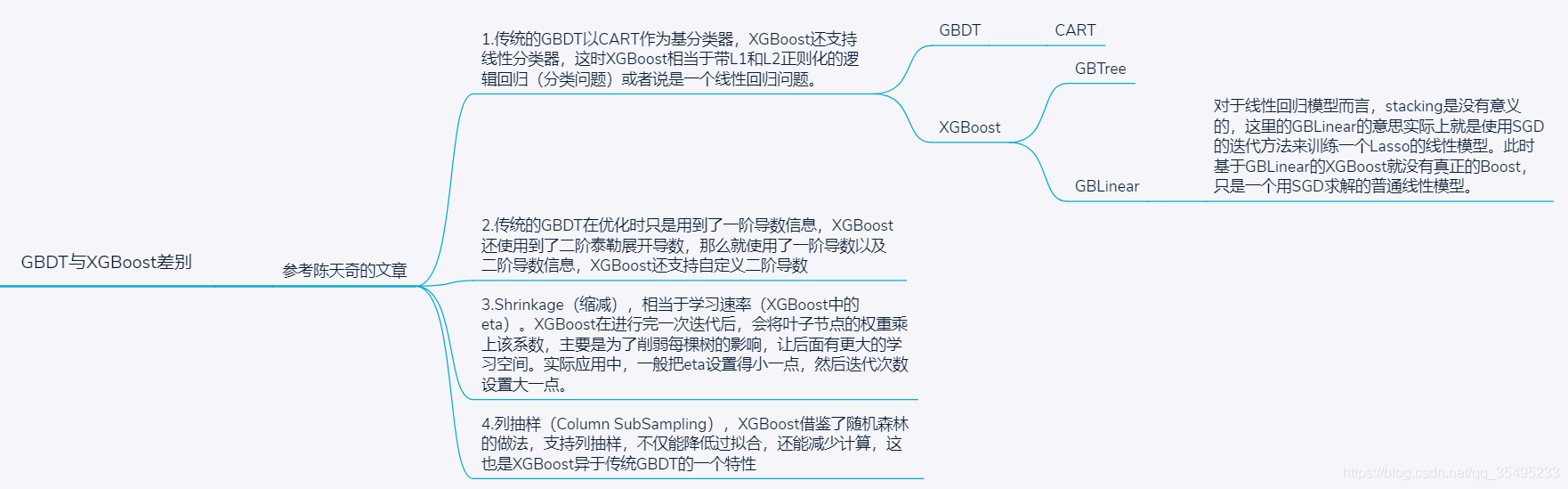
GBDTS={1.GBDT2.XGBoost GBDTS = \left\{\begin{array}{cc}
1. GBDT \\
\quad 2. XGBoost \end{array}\right.GBDTS={1.GBDT2.XGBoost
GBDT与XGBoost算法的优点就是提供了GPU版本,并能够处理一些离散特征。
2.CatBoost详解
CatBoost中被提及最多的就是Categorical Features就是一个离散特征与标签信息处理,最初CatBoost被设计出来就是为了来处理GBDT特征中的Categorical Features。如果在我们的数据中,在标签中没有使用discrete features(离散特征)的说法,也就是说,底层原始思想依然是CART,但是我们知道,CART是不能接收字符串作为离散特征的情况。
我们可以回顾下CART树,其是以基尼系数Gini来进行叶节点的分割,其中,我们以分类的问题来说,假设有k个类别,样本点属于第 kkk 类的概率为pkp_kpk,则样本概率分布的Gini指数定义为:
Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2Gini(p)=\sum_{k=1}^K {p_k(1-p_k)}=1-\sum_{k=1}^K p_k^2Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
Gini指数Gini(D,A)表示特征AAA不同分组的数据集DDD的不确定性。Gini指数值越大,样本集合的不确定性也就越大,这一点与熵的概念非常类似。但这里Gini是无法处理取值为字符串的离散特征,对于普通的连续或者离散特征而言,使用GBDT,我们在处理特征中的Categorical Features的时候,最简单的方法是使用对应标签的平均值来替换。如果在决策树中,标签平均值将作为节点分裂的标准,这种方法被称为Greedy Target-Based Statistics,简称Greedy TBS,用公式来表达就是:
∑j=1n[xj,k=xi,k]⋅Yj∑j=1n[xj,k=xi,k]\frac{\sum_{j=1}^n{[x_{j,k}=x_{i,k}]·Y_j}}{\sum_{j=1}^n[x_{j,k}=x_{i,k}]}∑j=1n[xj,k=xi,k]∑j=1n[xj,k=xi,k]⋅Yj
这种方法有一个显而易见的缺陷,就是通常特征比标签包含更多信息的时候,如果强行使用标签的平均值来表示特征的话,当训练集和测试集数据结果分布不一样时,就会出现条件偏移的问题。
一个标准改进Greedy TBS的方法是添加先验分布项,这样可以减少噪声和低频数据对于数据分布的影响:
∑j=1p−1[xσj,k=xσp,k]⋅Yσ,j+a⋅P∑j=1p−1[xσj,k=xσp,k]\frac{\sum_{j=1}^{p-1}{[x_{\sigma j,k}=x_{\sigma p,k}]·Y_{\sigma,j}+a·P}}{\sum_{j=1}^{p-1}[x_{\sigma j,k}=x_{\sigma p,k}]}∑j=1p−1[xσj,k=xσp,k]∑j=1p−1[xσj,k=xσp,k]⋅Yσ,j+a⋅P
上面的σj,k\sigma_j,kσj,k就是代表第jjj条数据,上面的kkk代表第kkk列也就是第kkk个特征,PPP是添加的先验项,aaa通常是大于0的权重系数。为了解决条件迁移的问题,我们在部分的训练数据上对数据的特征进行类似Greedy TBS的处理,而在第二个数据集合进行训练,CatBoost参考了在线学习的方法,首先对训练数据进行了重新排列,然后作为训练样本,而整个数据集合作为测试样本。
类似的,在GBDT的模型训练阶段,同样会因为训练数据与测试数据分布不同的问题产生预测偏移Prediction Shift和残差偏移Residual Shift的问题。为了解决
相应的问题,CatBoost作者采用了排序提升Ordered Boosting的方式,首先对所有的数据进行随机排列,然后在计算第i步残差的时候模型只利用了随机排列中的前i-1个样本 。





 CatBoost是一种由俄罗斯人提出的机器学习算法,尤其擅长处理离散特征。它提供GPU版本并能有效处理Categorical Features。与传统GBDT相比,CatBoost在处理标签中未使用的离散特征时,通过添加先验分布项减少噪声和数据分布不一致带来的影响。此外,它采用排序提升的方法解决训练数据与测试数据分布不同导致的预测偏移问题。
CatBoost是一种由俄罗斯人提出的机器学习算法,尤其擅长处理离散特征。它提供GPU版本并能有效处理Categorical Features。与传统GBDT相比,CatBoost在处理标签中未使用的离散特征时,通过添加先验分布项减少噪声和数据分布不一致带来的影响。此外,它采用排序提升的方法解决训练数据与测试数据分布不同导致的预测偏移问题。
















 680
680

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








