机器学习（五）模型评估

混淆矩阵（Confusion Matrix）

混淆矩阵（Confusion Matrix）中包含四种数据：
(T/F表示预测正确与否，P/N表示被预测为正例还是负例)

• TP：实际为正例，被预测为正例，预测正确
• FP：实际为负例，被预测为正例，预测错误
• FN：实际为正例，被预测为负例，预测错误
• TN：实际为负例，被预测为正例，预测正确

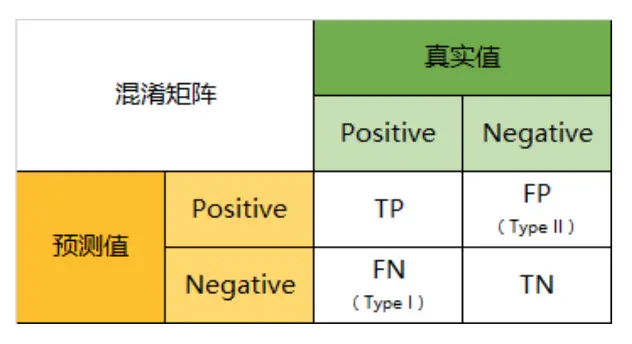
Confusion Matrix

由以上四种数据得到四种比率如下：

TPR（True Positive Rate，又称灵敏度：sensitivity）：TPR=TPTP+FN
，即正例被正确预测为正例的数目实际正例的数目
FPR（False Positive Rate）：FPR=FPFP+TN
，即负例被错误预测为正例的数目实际负例的数目
FNR（False Negative Rate）：FNR=FNTP+FN
，即正例被错误预测为负例的数目实际正例的数目
TNR（True Negative Rate，又称 特指度：specificity）：TNR=TNFP+TN
，即负例被正确预测为负例的数目实际负例的数目

评价指标

Precision，即查准率：P=TP/(TP+FP)
Recall，即查全率：R=TP/(TP+FN)
F-Score，即precision和recall的调和平均值，更接近precision和recall中较小的那一个值：F=2×P×R/(P+R)
Accuracy，分类器对整体样本的分类能力，即正例分为正例，负例分为负例：A=TP+TN/(TP+FP+FN+TN)

ROC曲线：

• 横坐标：假阳性率(FPR)，负样本中被预测为正样本的个数
• 纵坐标：真阳性率(TPR)，正样本中被预测为正样本的个数

---

如何绘制：

1. 统计正负样本数量：P/N
2. 横坐标刻度间隔：1/N
   纵坐标刻度间隔：1/P
3. 根据预测概率从高到低排序
4. (0, 0)开始
   遇到正样本，沿纵轴绘制一刻度；
   遇到负样本，沿横轴绘制一刻度；
   (1, 1)结束

---

和P-R曲线的区别

• 当测试集正负样本分布发生变化时，ROC曲线形状基本不变，而P-R曲线形状剧烈变化。

AUC

• 几何意义：ROC曲线下的面积大小，沿ROC横轴做积分。
• 物理意义：任取一对（正、负）样本，正样本预测分大于负样本的概率。对于AUC而言，并不关心具体预测的结果是标签或者概率，也不需要卡什么阈值，只要在预测结果之间有排序即可。
• 0.5到1之间。
• 如果一个模型好于另一个，则它的曲线下方面积相对较大。

---

参考资料
分类算法中常用的评价指标