重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

思路

前序遍历：根节点-左子树-右子树

中序遍历：左子树-根节点-右子树

后序遍历：左子树-右子树-根节点

1.前序遍历的第一个值为根节点的值

在中序遍历中找到根节点的值以及左右子树

1    2 4 7      3 5 6 8

4 7 2     1     5 3 8 6

2.在左右子树中可以找到各自的根节点

重复2过程，可以构建所有子树

               1

      2                        3

4                       5            6

   7                               8            

public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        TreeNode root=reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
        return root;
    }

    private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {
        if(startPre>endPre||startIn>endIn)
            return null;
        TreeNode root=new TreeNode(pre[startPre]);
         
        for(int i=startIn;i<=endIn;i++)
            if(in[i]==pre[startPre]){
                root.left=reConstructBinaryTree(pre,startPre+1,startPre+1+((i-1)-startIn),in,startIn,i-1);
                root.right=reConstructBinaryTree(pre,endPre-(endIn-(i+1)),endPre,in,i+1,endIn);
                      break;
            }
                 
        return root;
    }
}

 

 

 

 

拓展1：前序遍历和中序遍历         中序遍历和后序遍历可以确定一颗二叉树    （前序遍历和后续遍历不能确定一颗二叉树）

简单证明：一颗只有左子树的树和一颗只有右子树的树前序，构造的树相同，但却不是同一棵树

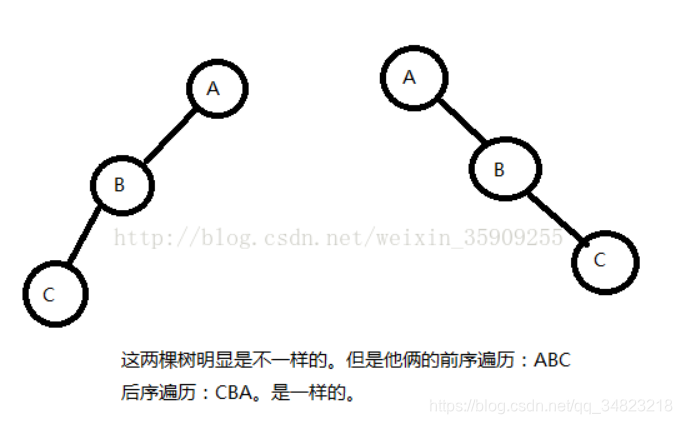
拓展2：根据中序遍历和后序遍历构造一颗二叉树

public class Solution {
    public TreeNode reConstructBinaryTree(int [] in,int [] aft) {
        TreeNode root=reConstructBinaryTree(in,0,in.length-1,aft,0,aft.length-1);
        return root;
    }

    private TreeNode reConstructBinaryTree(int [] in,int startIn,int endI,intn [] in,int startAft,int endAft) {
        if(startAft>endAft||startIn>endIn)
            return null;
        TreeNode root=new TreeNode(pre[endAft]);
         
        for(int i=startIn;i<=endIn;i++)
            if(in[i]==pre[endAft]){
                root.left=reConstructBinaryTree(in,startIn,i-1,aft,startAft,startAft+((i-1)-startIn));
                root.right=reConstructBinaryTree(in,i+1,endIn,aft,endAft-1-(endIn-(i+1)),endAft-1);
                      break;
            }
                 
        return root;
    }
}

 

 

（部分引用自：https://blog.youkuaiyun.com/weixin_35909255/article/details/55071068）