海明校验码

• 海明码是基于偶校验的扩展，将信息位分组进行偶校验
• 海明码可以针对一位跳变，进行纠错（指明那一位出了错，就是纠错，因为非0即1）
• 针对两位跳变，海明码可以检错
• 海明码原理
  • 将所有的信息位分组，保证，所有的组都有一个全部重叠，都有一个不重叠，也就是2进制的分组
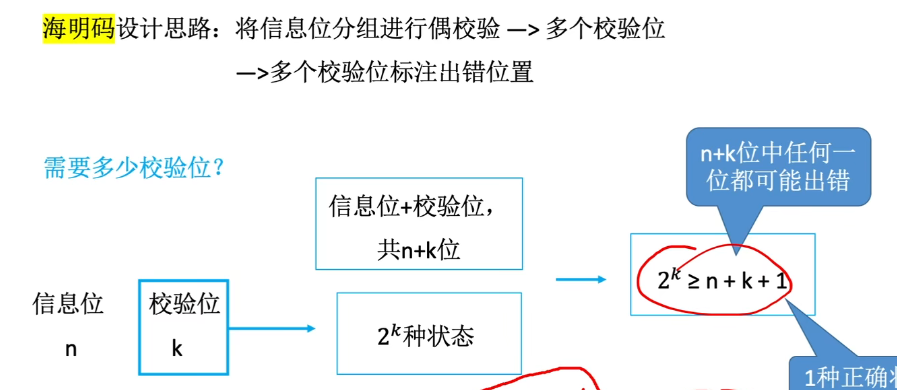
  • 每个分组一个校验位进行标识，总的bit数就是n+k （2^k > n+k）
  • 所有的校验位可以标识当前出错的一个bit
  • 这个原理和小白鼠试毒很像，也是分组，老鼠那里是10只老鼠试1000瓶药，一瓶有毒，2的10次方刚好可以表示1024，每个老鼠对应10bit中的一位，对第0瓶到底999瓶，把10进制数转换成二进制，哪个位为1，哪只老鼠喝，最终死的老鼠都喝过那瓶药，没死的说明没有毒，用这种分组的方式，重叠，最终看组的结果，从而确定是哪一个瓶子有毒
  • 除此之外，海明码的校验位必须放在1,2,4,8,16.。2的次方上（原点从1开始），这样放置是为了保证分组中，没有校验位，全是信息位
  • 小白鼠那个是二分法，实际这里也是二分法
• 此时的海明码只能解决1位的纠错，但对于部分的两位跳变，还不能处理，所以该海明码n+k加上一个偶校验位，从而使得能够对两位跳变校验
  • 偶校验为0，海明校验位都为0，说明没有问题
  • 偶校验为1，海明校验位非0，说明一位跳变，可以纠错
  • 偶校验为0，海明校验非0，说明两位跳变，此时校验知错，无法处理，需要重传
  • （因此，总共需要2^k>n+k+1）
• 对于三位跳变的情况，这种无法处理，但实际上概率也非常的低
• 
• 
• 
• 
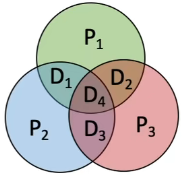
• 把这里的p和d换成h，就能更好理解了