排序算法（5）堆排序

一:基本思想

堆排序是利用堆（一种近似完全二叉树的结构）这种数据结构设计的一种排序算法

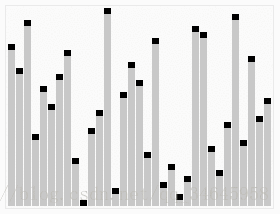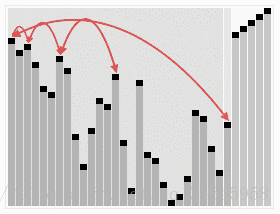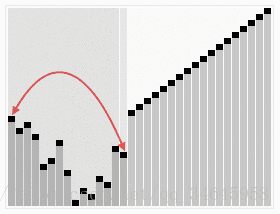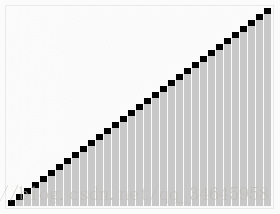
（1）由输入的无序数组构造一个最大堆，作为初始的无序区

（2）把堆顶元素（最大值）和堆尾元素进行互换

（3）把堆的尺寸缩小1，并调用heapify（A,0）从新的堆顶元素开始进行堆调整

（4）重复步骤（2），直到堆的尺寸为1

二.概览

分类：内部比较排序

数据结构：数组

最差时间复杂度：O（nlogn）

最优时间复杂度：O（nlogn）

平均时间复杂度：O（nlogn）

所需辅助空间：O（1）

稳定性：不稳定（不稳定发生在栈顶元素与a[i]交换的时候）

               比如序列：{ 9, 5, 7, 5 }，堆顶元素是9，堆排序下一步将9和第二个5进行交换，得到序列 { 5, 5, 7, 9 }，再进行堆调整得到{ 7, 5, 5, 9 }，重复之前的操作最后得到{ 5, 5, 7, 9 }从而改变了两个5的相对次序。

三.代码实现

public class Heap {
    //交换函数
    public static void Swap(int A[], int i, int j)
    {
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }
    //建堆
    public static int BuildHeap(int a[]){
        int heap_size = a.length;
        for (int i = heap_size/2-1;i >=0;i--){
            heapify(a,i,heap_size );
        }
        return heap_size;
    }
    //堆调整
    public static void heapify(int a[],int i,int size){
        int left_child = 2*i +1;  //左孩子索引
        int right_child = 2*i + 2; //右孩子索引
        int max = i;
        if(left_child<size && a[left_child]>a[max]){
            max = left_child;
        }
        if(right_child<size && a[right_child]>a[max]){
            max = right_child;
        }
        if (max != i){
            Swap(a, max, i); //把当前结点和它的最大子结点进行互换
            heapify(a, max, size);//递归调用，继续从当前结点向下调整（注意下是指根）
        }
    }
    //堆排序
    public static void sort(int a[]){
        //建立一个大堆
        int heap_size = BuildHeap(a);
        while (heap_size > 1){ // 大于1表示未完成排序
            //将堆顶元素与最后一个元素交换，并从堆中去掉最后一个元素
            //此处的交换很可能把后面的元素的稳定性打乱，所以堆排序不是稳定的排序
            Swap(a, 0, --heap_size);
            //从新的堆顶元素开始向下调整，时间复杂度o(logn)
            heapify(a, 0, heap_size);
        }
    }
    
}