40、两数相除

题目描述：

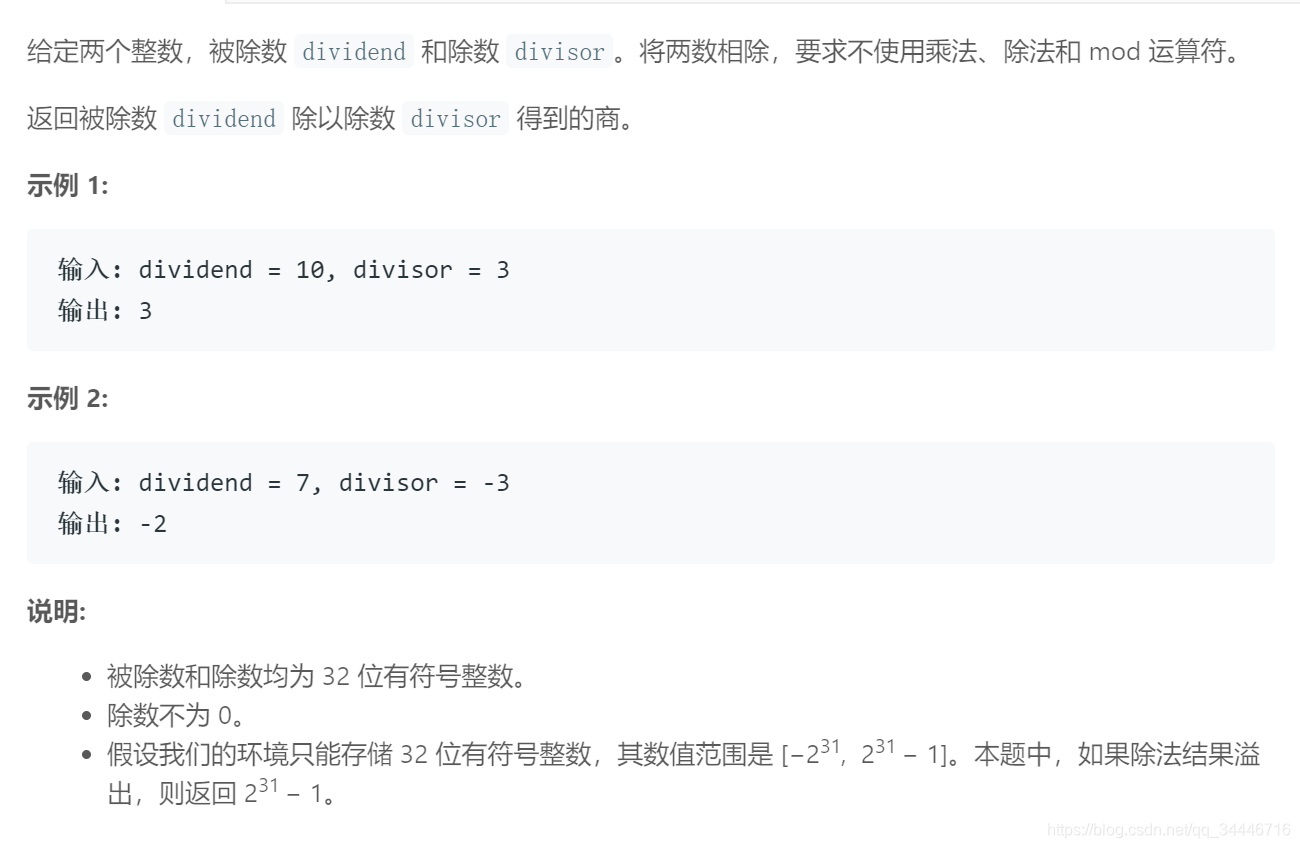
这道题使用普通解法会出现一系列的bug，并且使用减法会超时
因此考虑使用位运算
思路：
当被除数大于等于除数时(否则的话就为0了)，我们设置两个变量t和p，并分别初始化为除数和1(最小的情况)，当被除数大于等于t的二倍时，将t和p同时扩大二倍(左移)，并将返回值加上p，除数减去t。拿十进制举例:29除以8，8扩大二倍，16小于29，再扩大二倍，超过29，于是29减去之前的16，返回值加上2。第二次循环时因为此时的13小于8的二倍，故加上1，整个循环结束，最终结果为2+1=3，符合要求。此外还要注意判断结果正负号时亦或的作用。

原文：https://blog.youkuaiyun.com/Windows_Defender/article/details/80445969
代码：

class Solution {
    public int divide(int dividend, int divisor) {
        if (dividend == 0) {
            return 0;
        }
        
        if (dividend == Integer.MIN_VALUE && divisor == -1) {
            return Integer.MAX_VALUE;
        }
        
        boolean isPositive = true;
        if (dividend > 0 && divisor < 0 || (dividend < 0 && divisor > 0)) {
            isPositive = false;
        }
        
        long a = Math.abs((long) dividend);
        long b = Math.abs((long) divisor);
        int shift = 0;
        int result = 0;
        
        while (a >= b) {
            while (a >= b << shift) {
                shift++;
            }
            a -= b << (shift - 1);
            result += 1 << (shift - 1);
            shift = 0;
        }
        
        return isPositive ? result : -result;
    }
}