3、镜面反射（Weekly Contest 90）

最新推荐文章于 2022-10-02 17:09:22 发布

原创最新推荐文章于 2022-10-02 17:09:22 发布 · 177 阅读

0 ·

CC 4.0 BY-SA版权

竞赛专栏收录该内容

253 篇文章

订阅专栏

本文探讨了一种解决正方形内光线反射路径问题的算法。通过分析反射规律，将复杂问题简化，利用数学方法找到光线首次落在正方形特定点上的最短路径。代码实现了三种可能的落点情况，并通过计算最小公倍数优化效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：
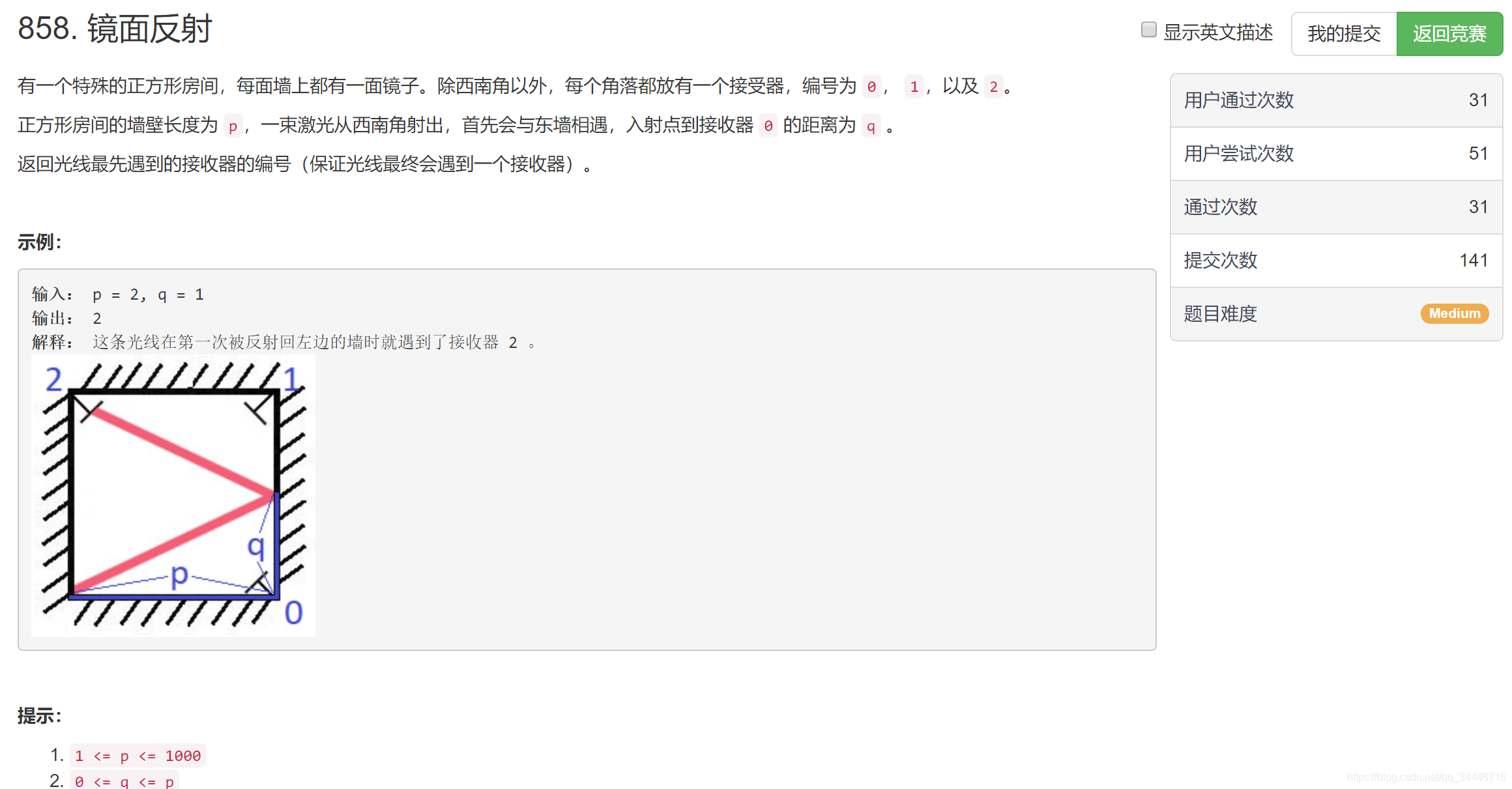
在这里插入图片描述

我是直接根据题意来的，丝毫没有进行转化，因此可能有点复杂，只是将反射进行了转化，即不考虑上下的反射，只考虑左右，将正方形上下延长即可
代码如下：

class Solution {
    public int mirrorReflection(int p, int q) {
        //根据画图我们知道每次走的距离是固定的，只不过第一次走的是q，第二次走的是 2 * q，画图可以很明显看出来
		if(2 * q == p){
			return 2;
		}
		if(p == q)
			return 1;
		int time1 = 1;
		int time2 = 1;
		int time0 = 1;
		//判断落在2上最小距离
		while ( (time2 * 2 * q + p ) % (2 * p) != 0) {
			time2 ++;
			if(time2 >= 10000){
				break;
			}
		}
		int tem2 = time2 * 2 * q;
		System.out.println("2的距离为：   "+  tem2);
		while ((time1 * 2 * q + q + p) % (  2 * p) != 0 ){
			time1++;
			if(time1 >= 10000){
				break;
			}
			if(time1 > time2){
				break;
			}
		}
		int tem1 = time1 * 2 * q + q;
		System.out.println("1的距离为：   "+  tem1);

		//只有这种情况是最好弄的，其余都需要转
		while ((time0 * 2 * q + q) % ( 2 * p ) != 0) {
			time0 ++;
			if(time0 > time1 || time0 > time2){
				break;
			}
			if(time0 >= 10000){
				break;
			}
		}
		int tem0 = time0 * 2 * q + q;
		System.out.println("0的距离为：   "+  tem0);

		if(tem0 < tem1 && tem0 < tem2){
			return 0;
		}else if (tem1 < tem0 && tem1 < tem2) {
			return 1;
		}else {
			return 2;
		}
        
        
    }
}

但是速度太慢了

class Solution {
    public int mirrorReflection(int p, int q) {
        int minCommonMultiple = p * q / maxCommonDivisor2(p,q);
        int multi = minCommonMultiple / q;
        if (multi % 2 == 0) {
            return 2;
        }else {
            int x = minCommonMultiple / p;
            if (x % 2 == 0) {
                return 0;
            }else {
                return 1;
            }
        }
    }
    private int maxCommonDivisor2(int m, int n) {
        // 保证m>n,若m<n,则进行数据交换
        if (m < n) {
            int temp = m;
            m = n;
            n = temp;
        }
        // 在余数不能为0时,进行循环
        while (m % n != 0) {
            int temp = m % n;
            m = n;
            n = temp;
        }
        // 返回最大公约数
        return n;
    }
}