本实验使用mnist数据集完成手写数字识别的测试。识别正确率认为是95%
完整代码如下:
#!/usr/bin/env python
# coding: utf-8
# In[1]:
import numpy
import scipy.special
import matplotlib.pyplot
# In[2]:
class neuralNetwork:
def __init__(self, inputNodes, hiddenNodes, outputNodes,learningRate):
self.iNodes = inputNodes
self.oNodes = outputNodes
self.hNodes = hiddenNodes
self.lr = learningRate
self.wih = numpy.random.normal (0.0, pow(self.hNodes,-0.5), (self.hNodes, self.iNodes))
self.who = numpy.random.normal (0.0, pow(self.oNodes,-0.5), (self.oNodes, self.hNodes))
self.activation_function = lambda x: scipy.special.expit(x)
#print(self.wih)
pass
def train(self,inputs_list, target_list):
inputs = numpy.array(inputs_list, ndmin=2).T
targets = numpy.array(target_list, ndmin=2).T
#print(inputs)
#print(targets)
hidden_inputs = numpy.dot(self.wih,inputs)
#print(self.wih.shape)
#print(inputs.shape)
hidden_outputs = self.activation_function(hidden_inputs)
#print(hidden_inputs)
final_inputs = numpy.dot(self.who,hidden_outputs)
#print(hidden_outputs)
final_outputs = self.activation_function(final_inputs)
output_errors = targets - final_outputs
hidden_errors = numpy.dot(self.who.T,output_errors)
self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)),numpy.transpose(hidden_outputs))
self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)),numpy.transpose(inputs))
pass
def query(self, inputs_list):
inputs = numpy.array(inputs_list, ndmin=2).T
hidden_inputs = numpy.dot(self.wih,inputs)
hidden_outputs = self.activation_function(hidden_inputs)
final_inputs = numpy.dot(self.who,hidden_outputs)
final_outpus = self.activation_function(final_inputs)
return final_outpus
pass
# In[3]:
inputNodes = 784
outputNodes = 10
hiddenNodes = 100
learningRate = 0.1
nN = neuralNetwork(inputNodes, hiddenNodes, outputNodes, learningRate)
# In[4]:
data_file = open("mnist_train.csv",'r')
data_list = data_file.readlines()
data_file.close()
# In[5]:
epochs = 1
for e in range(epochs) :
for record in data_list:
all_values = record.split(',')
inputs = numpy.asfarray( all_values [1:])/255.0*0.99+0.01
targets = numpy.zeros(outputNodes) + 0.01
targets[int (all_values[0])] = 0.99
nN.train(inputs,targets)
pass
pass
# In[6]:
test_data_file = open("mnist_test.csv",'r')
test_data_list = test_data_file.readlines()
test_data_file.close()
# In[7]:
scorecard = []
for record in test_data_list:
all_values = record.split(',')
correct_label = int(all_values[0])
inputs = numpy.asfarray( all_values [1:])/255.0*0.99+0.01
outputs = nN.query(inputs)
label = numpy.argmax(outputs)
if(label == correct_label):
scorecard.append(1)
else:
scorecard.append(0)
pass
pass
# In[8]:
scorecard_array = numpy.asarray(scorecard)
print ("performance = " ,scorecard_array.sum()/scorecard_array.size)
# In[9]:
import scipy.misc
img_array = scipy.misc.imread('test.png',flatten="True")
img_data = 255.0 - img_array . reshape(784)
img_data = (img_data /255.0 * 0.99 ) + 0.01
op=nN.query(img_data)
print(op)
print(numpy.argmax(op))
# In[10]:
all_values = data_list[1].split(',')
image_array = numpy.asfarray( all_values [1:]).reshape((28,28))
matplotlib.pyplot.imshow(image_array, cmap = 'Greys',interpolation='None')
IN[9]到IN[10]的代码分别用于测试自己制作的数字识别效果和显示图像。可去掉。代码运行过程需要mnist数据集。
BP神经网络的结构:
BP神经网络的简单结构:输入层、一个或者多个隐层、输出层。图如下:
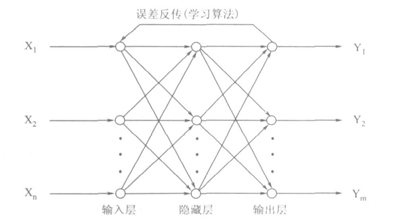
在图中,涉及到的参数有:X1--Xn为输入参数。输入参数通过输入层和隐层之间的的链接权重进行计算,到达隐层。
隐层的输入参数通过隐层自带的激活函数到达隐层的输出参数
隐层的输出参数通过隐层和输出层的链接权重进行计算到达输出层的输入
输出层的输入参数通过输出层自带的激活函数到达输出层的输出参数,即为输出结果
将输出结果与期望结果进行对比,得出误差。
将误差反向传递到神经网络中,改变神经网络的层之间的权值,即训练神经网络。
训练结束后,从输入层输入参数,得到输出参数,进行测试。
在输入层的神经元数据选取上,和像素数量一致。MNIST采用28X28的像素点,则输入层的神经元数量为28*28=784个
输入层和隐层,输出层和隐层之间的权值选取为随机数。使用正态分布的随机数较好。
隐层的神经元数量合适即可,取值为经验法,假设为100个
输出层神经元表示数据0-9,则使用10个神经元,分别表示数字0-9的可能性概率。
训练过程中使用的学习效率,取0.2吧。。。
将权重,各层神经元值,误差等,表示为矩阵数据进行处理。
正向传递数据查询结果,误差的反向传递改变权重等过程,涉及到的数学推导:
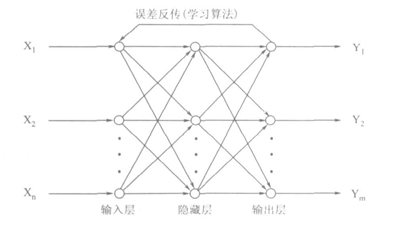
输入数据X1-Xn。
输入层和隐层之间的权Wji
隐层的输入数据为:∑iwjixi
隐层的输出数据为:yj = f(∑iwjixi)。其中f(x)=![]()
隐层的输入数据为:∑jwkjyj
隐层的输出数据为:yk = f(∑jwkjyj)。。其中f(x)=![]()
对应到代码中的query部分。
训练神经网络时,首先查询神经网络,计算出误差。
误差矩阵根据上一次的权重比例,分割误差,采用梯度下降法,确定调整的权重数值,配合学习率。完成训练神经网络。





 本文介绍了一个基于BP神经网络的手写数字识别系统,使用mnist数据集进行训练和测试,最终识别准确率达到95%。系统详细展示了神经网络的结构、权重初始化、前向传播和反向传播的过程。
本文介绍了一个基于BP神经网络的手写数字识别系统,使用mnist数据集进行训练和测试,最终识别准确率达到95%。系统详细展示了神经网络的结构、权重初始化、前向传播和反向传播的过程。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










