剑指Offer_重建二叉树

题目描述：

    输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

思路：对于给定的两种排序的结果，只要其中含有中序，换句话说，只有是中序加上前序或后序，我们就可以把这颗二叉树还原出来，拿这题来说，给出了  

            前序：根 左 右

            中序：左 根 右

        那么对于这个序列，前序排列中第一个数就是根，再拿这个根与中序遍历结果比较，找到中序中的根的位置，那么，就可以算出，这个根的左子树的长度，右子树的长度。再结合，前序排列，就知道了 ，左子树的 前序排列 ，左子树的中序排列，右子树的 前序排列 ，右子树的 中序排列； 前序遍历这个循环即可得到结果；

        

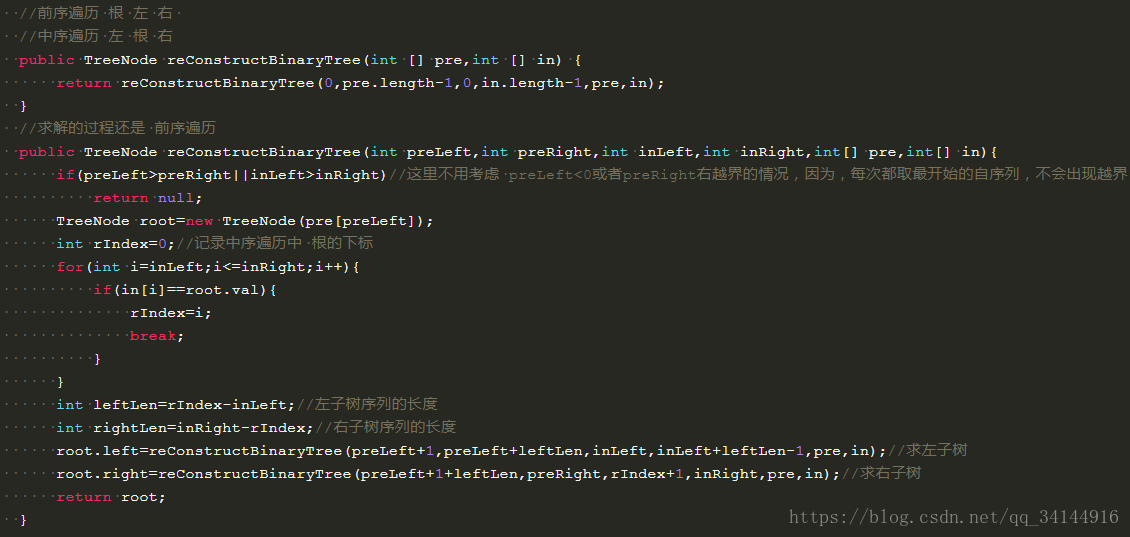
Copy版：

//前序遍历 根 左 右 
    //中序遍历 左 根 右
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        return reConstructBinaryTree(0,pre.length-1,0,in.length-1,pre,in);
    }
    //求解的过程还是 前序遍历
    public TreeNode reConstructBinaryTree(int preLeft,int preRight,int inLeft,int inRight,int[] pre,int[] in){
        if(preLeft>preRight||inLeft>inRight)//这里不用考虑 preLeft<0或者preRight右越界的情况，因为，每次都取最开始的自序列，不会出现越界
            return null;
        TreeNode root=new TreeNode(pre[preLeft]);
        int rIndex=0;//记录中序遍历中 根的下标
        for(int i=inLeft;i<=inRight;i++){
            if(in[i]==root.val){
                rIndex=i;
                break;
            }
        }
        int leftLen=rIndex-inLeft;//左子树序列的长度
        int rightLen=inRight-rIndex;//右子树序列的长度
        root.left=reConstructBinaryTree(preLeft+1,preLeft+leftLen,inLeft,inLeft+leftLen-1,pre,in);//求左子树
        root.right=reConstructBinaryTree(preLeft+1+leftLen,preRight,rIndex+1,inRight,pre,in);//求右子树
        return root;
    }