java并查集 - Kaiqisan

大家好，都吃晚饭了吗？我是Kaiqisan,是一个已经走出社恐的一般生徒,最近被力扣的每日一题给整破防了，天天都是并查集，我麻了！所以最近都在学习并查集，现在终于搞懂了，于是有了这篇博客！

想要代码的直接通过目录超链接熬

什么是并查集

首先是明确概念

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。
并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。常常在使用中以森林来表示。
– 以上内容来自百度百科 https://baike.baidu.com/item/%E5%B9%B6%E6%9F%A5%E9%9B%86/9388442?fr=aladdin

再举个例子

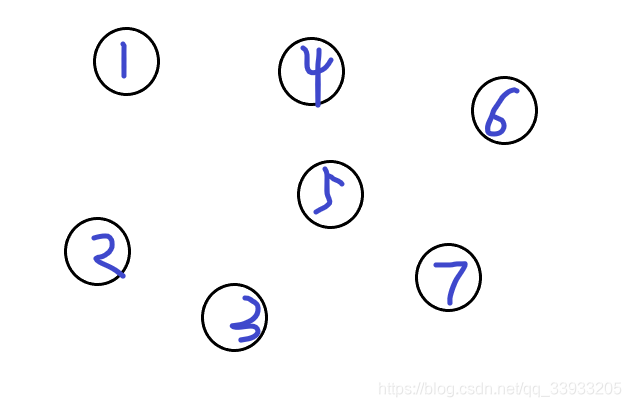
上面有七个节点，我们通过某种方法把它们其中的一些连在一起（[1 <-> 4] [5 <-> 4] [1 <-> 2] [6 <-> 7] [3 <-> 7]）
(有点像无向图）

上面的所有的节点就拥有了两个结合（1245一个集合 367一个集合）

此时并查集的功能一个功能就是判断两个节点是否在一个集合

比如我现在随便捉两个节点 2 4 我们就可以通过并查集判断它们是一个集合

也可以判断所有的节点一共组合成了多少集合（显然，图中有2个集合）

代码实现

好了，基本概念我们都明白了，我们现在要如何实现它呢？

首先是判断一个点是否属于一个集合，我们可以在一个集合中设置一个代表节点，让所有的节点都指向这个节点。或者同一个集合内所有节点的最终指向都会追溯到这个代表节点

我们现在再以两个节点 2 4 为例，现在我们就可以通过这个箭头找到同一个代表节点1，我们就可以判断两个节点2 4是属于同一个

同理，我们再以两个节点 5 7为例，通过指针，5节点找到了1，7节点找到了3，所以这两个节点不是在一个集合中的

以上是两个节点的查找，然后我们再来看两个节点的链接

在一开始的时候，肯定是所有的节点都是孤单的，需要我们来连起来

我们默认一个数组arr = [0, 1, 2, 3, 4, 5, 6] （注： arr下标表示节点次序，值表示指针指向的那个节点）

还有一个size数组 [1, 1, 1, 1, 1, 1, 1]

表示被指针指向的次数，此时所有的节点都被自己的指针指了一次，所以都是1

此时，所有节点的指针都指向自己，各自为各自的集合

现在有 [0 <-> 1]

现在现场一无所有，我们就默认后面的连接前面的

此时1的指针改变， 1和0就构成了一个集合，现场的集合总数-1

存储指针信息的数组arr变成

[0, 0, 2, 3, 4, 5, 6]

然后是size变成了

[2, 1, 1, 1, 1, 1, 1]

Ps:虽然1节点没有被指针指了，但是size并不减少

以上就是常规的连接流程
接下来就是探讨一些特殊情况的时候了！

---

经过多次连接，现在图变成这样了

显而易见

此时的arr为 [0, 0, 0, 3, 0, 5, 6] size为 [4, 1, 1, 1, 1, 1, 1]

现在有 [3 <-> 4]

首先，我们通过节点3和节点4的指针找到它们的代表节点，最终节点4找到了节点0，节点3还是指向自己所以没有任何变动，
然后我们试图通过默认的方式把节点0的指针连接到节点3上（如图）

但是咱不能这么做，在连接之前，我们还需要判断两个节点对应的size大小，通过上面的size数组 [4, 1, 1, 1, 1, 1, 1] 我们得知，节点0的size碾压节点3的size，所以只能把上面的连接翻转一下！

---

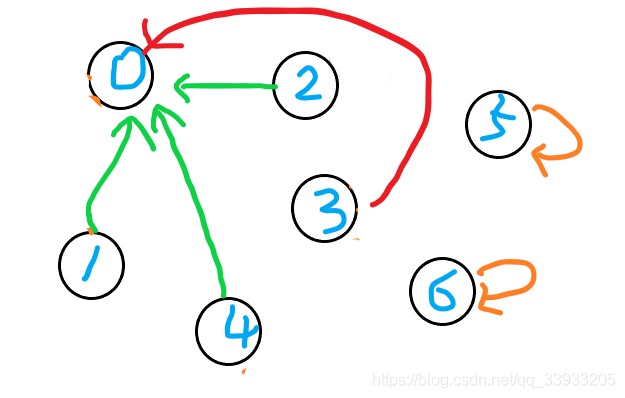
下面的例子也是同上的原理

通过图我们得知指针数组arr为 [0, 0, 0, 0, 0, 5, 5, 5] size指针为 [5, 1, 1, 1, 1, 3, 1, 1]

接下来，我们来见证一个奇迹

我们连接下 6 和 4 把 ！ 也就是 [6 <-> 4]

首先我们还是先找一找集合的代表节点

通过指针我们知道 节点6 的代表节点是5 节点4的代表节点为 0，还是那个问题，到底是 5连接0 还是0连接5呢

这由它们的size决定

好家伙

0的size更胜一筹

所以5要去连接0

结果图变成这样了

---

所以有了并查集，我们在一个集合中搜索一个节点在一个集合里面的代表节点的时候它的时间复杂度为 O（1），很快的！

优化

对于上面这张图，存在一些节点(6 7) 这些节点无法直接找到代表节点，需要按照路径 (6 -> 5 -> 0)多走了一步，所以这张图还有优化的空间！

需要再次搜索来优化

这样就有所有的节点都直接指向一个代表节点了。

代码

成员是数字（在实际使用的时候回碰到对象数组，用这里的数字代表下标就可以了！）

class UnionFind {
    int n;
    int[] parent;
    int[] size;
    int group;  // 组别

    public UnionFind(int n) {
        this.parent = new int[n];
        this.n = n;
        this.size = new int[n];
        this.group = n;
        Arrays.fill(size, 1); // 所有元素填充为1
        for (int i = 0; i < n; i++) {
            this.parent[i] = i;
        }
    }

	// 找代表节点
    public int find(int x) {
        return parent[x] == x ? x : (parent[x] = find(parent[x]));
    }

	// 连接两个节点
    public boolean unite(int x, int y) {
        x = find(x);
        y = find(y);
       
        if (x == y) { // 已经在一个集合里了，没必要再连了
            return false;
        } else {
        	// 先判断两个代表节点的size决定是否要翻转指针
            if (size[x] < size[y]) {
                int temp = x;
                x = y;
                y = temp;
            }
            parent[y] = x;
            size[x] += size[y];
            group--;
            return true;
        }
    }

	// 判断两个节点是否在一个组里
    public boolean isConnected(int x, int y) {
        x = find(x);
        y = find(y);
        return x == y;
    }
}

成员是对象

class UnionFindForMore<T> {
    int n;
    int[] parent;
    int group;  // 组别
    public HashMap<T, T> fatherMap;
    public HashMap<T, Integer> sizeMap;

    public UnionFindForMore(T[] list) {
        this.parent = new int[list.length];
        this.n = list.length;
        this.group = list.length;
        // 初始化，先指向自己
        for (T item : list) {
            fatherMap.put(item, item);
            sizeMap.put(item, 1);
        }
    }

    public T find(T node) {
        // 递归
//        T father = fatherMap.get(node);
//        if (father != node) {
//            father = find(father);
//        }
//        fatherMap.put(node, father);
//        return father;
        // 非递归 --- 优点：不用再一次整合指针
        Stack<T> stack = new Stack<>();
        T temp = node;
        T parent = fatherMap.get(temp);
        while (temp != parent) {
            stack.push(temp);
            temp = parent;
            parent = fatherMap.get(temp);
        }
        while (!stack.isEmpty()) {
            fatherMap.put(stack.pop(), parent);
        }
        return parent;
    }

    public boolean unite(T x, T y) {
        if (x == null || y == null) {
            return false;
        }
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        } else {
            int size1 = sizeMap.get(x);
            int size2 = sizeMap.get(y);
            // 可以不使用temp来优化内存
            if (size1 < size2) {
                T temp = x;
                x = y;
                y = temp;
            }
            fatherMap.put(y, x);
            sizeMap.put(x, size1 + size2);
            group--;
            return true;
        }
    }

    public boolean isConnected(T x, T y) {
        x = find(x);
        y = find(y);
        return x == y;
    }
}

总结（谈人生）

并查集还是比较好理解的，我觉得最重要的还是这个size的判断，当时刷力扣看题解的时候卡在这里好久了，size其实就是拿来完善并查集组合的指针方向一致性的。最近力扣的并查集轰炸也快结束了，我们还得整装待发学习其他知识了！

其实脱开并查集，来康康我们的人生，其实不管在我们的人生还是仕途中，我们每个人都是一个普普通通的节点，我们有各自的圈子，各种圈子就是各种集合，所有的集合就构成了我们的社会。
我们来窥探一下集合，在每一个集合中，必然有一个节点是所有的节点的指针指向的终点，犹如众星拱月一般被高高捧起的存在（俗称大佬）可是，大佬何为大佬，可大佬在一开始的时候也不是大佬，就如刚刚说的，大家在一开始的时候都是一个普普通通的节点，所以，大佬的诞生就在不断的合并节点中形成的，自己通过不断的努力，不断地积累知识来丰裕自己，让自己比其他人更加优秀，让其他节点都开始指向自己，让自己小有规模（变成小佬？），以上是和人之间的竞争。有集合就必有图，集合是在社会这个大前提下存在的，所以我们也无法避免和其他大佬之间的较量，较量的结果只有输或者赢，输了的话自己就必须牺牲自己的指针指向别人，赢了才能获得别人的指针（有点大鱼吃小鱼的意味，这里话可能说得有点绝对（失败一次就彻底没有第二次竞争（合并节点）的机会了），不要杠我！我是好孩子，但其实社会不就是这般弱肉强食吗？成年人的世界没有对错，只有无止境的利益）。在不断的竞争中，能成为一个集合代表节点的都是已经手身经百战的强强手，手下掌握着奇多无比的节点，如此高调的他给人们留下深刻的印象，成为了行业的天花板，也就顺势赢得了尊重与褒奖…

所以说

在这个社会中，我们从来不要去惧怕竞争（合并节点），大家都在努力往上爬，如果停滞不前，那岂不是和咸鱼有什么区别（不喜欢讲道理，讲道理环节到此结束！）

今天的博客写到这里，如果觉得还是无法理解并查集的可以看看上面的小故事，辅助理解熬

如果觉得这篇博客还不错的，别忘了点个赞收个藏唷！爱你们！ε=(´ο｀*))（以前都从没要过赞，今天这篇真的真的写了很久！）