图的存储结构
1邻接矩阵表示法
存储方式是用两个数组来表示图,一个一维数组表示图中顶点的信息,一个二维数组表示存储图中的边的信息。
即边采用顺序存储结构,用二维数组存储,称为图的邻接矩阵
1.1 无向图邻接矩阵表达
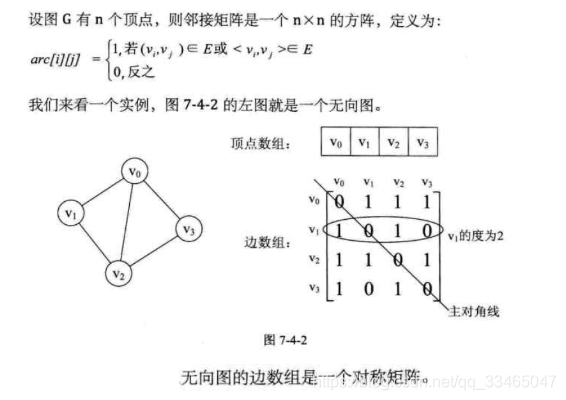
无向图,邻接矩阵一定是对称的,而且对角线一定为0
1.2 有向图邻接表达
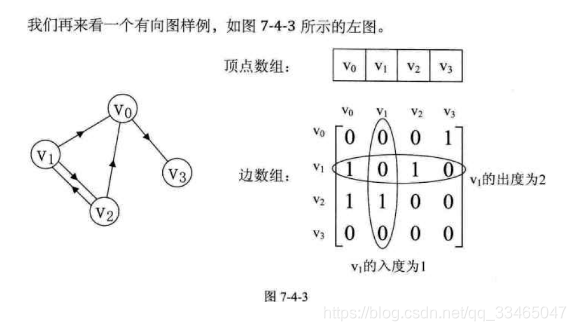
1.3带权邻接表达,对顶点之间没有联系的,用无穷大表示。
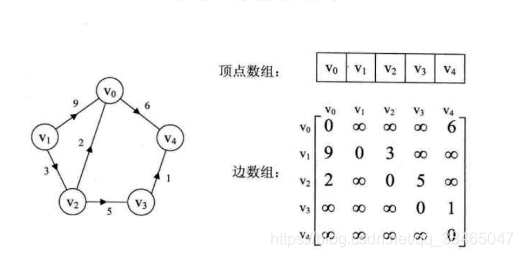
分析可得:
- 在无向图的邻接矩阵中的第i 行或者第i 列的非零元素的个数,为第i个顶点的度;
- 在有向图中邻接矩阵中的第i行的非00元素的个数为第i个顶点的出度,第i行非00元素的个数为第i个顶点的入度。
- 无向图的邻接矩阵是对称的。
- 有向图的邻接矩阵不一定是对称的。
实例
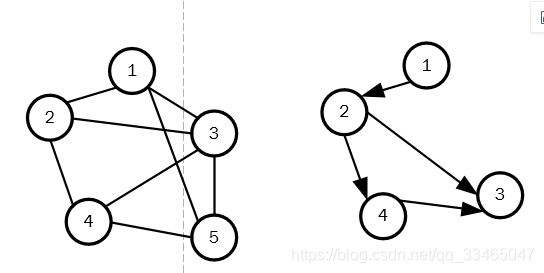
arr=[[0]*6 for row in range(6)] #声明矩阵arr
#图各边的起点值和终点值
data=[[1,2],[2,1],[1,5],[5,1], \
[2,3],[3,2],[2,4],[4,2], \
[3,4],[4,3]]
for i in range(10): #读取图的数据
for j in range(2): #填入arr矩阵
for k in range(6):
tmpi=data[i][0] #tmpi为起始顶点
tmpj=data[i][1] #tmpj为终止顶点
arr[tmpi][tmpj]=1 #有边的点填入1
print('无向图矩阵:')
for i in range(1,6):
for j in range(1,6):
print('[%d] ' %arr[i][j],end='') #打印矩阵内容
print()
无向图矩阵:
[0] [1] [0] [0] [1]
[1] [0] [1] [1] [0]
[0] [1] [0] [1] [0]
[0] [1] [1] [0] [0]
[1] [0] [0] [0] [0]
有向图
arr=[[0]*6 for row in range(6)] #声明矩阵arr
data=[[1,2],[2,1],[2,3],[2,4],[4,3],[4,1]] #图各边的起点值和终点值
for i in range(6): #读取图的数据
for j in range(6): #填入arr矩阵
tmpi=data[i][0] #tmpi为起始顶点
tmpj=data[i][1] #tmpj为终止顶点
arr[tmpi][tmpj]=1 #有边的点填入1
print('有向图矩阵:')
for i in range(1,6):
for j in range(1,6):
print('[%d] ' %arr[i][j],end='') #打印矩阵内容
print()
2 领接表表示法
边采用链式存储结构,存储行的后继,即矩阵行的单链表,称为图的邻接表。
用链式存储结构存储图,是由一个顺序存储的顶点表和多个链式存储的边表组成的,边表的个数和图的顶点个数相同。
顶点表由顶点组成,每个顶点节点又由数据域和指针域组成。数据域存放顶点值,指针域指向边表中的第一个边节点。边表由边节点组成。
分为两部分:
第一部分:图中的每一顶点及与该顶点相关联的第一条边或弧;
第二部分:与某一顶点相关联的所有边,或某一顶点为弧尾的所有弧。
2.1无向图的领接表
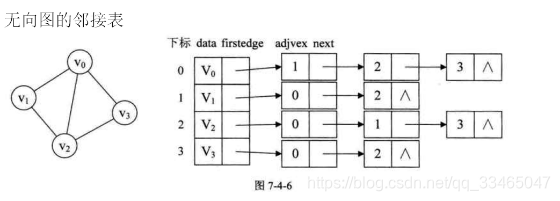
2.2 有向图的领接图
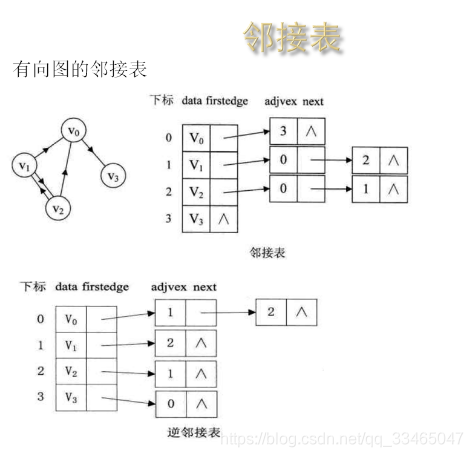
2.3 带权的邻接图
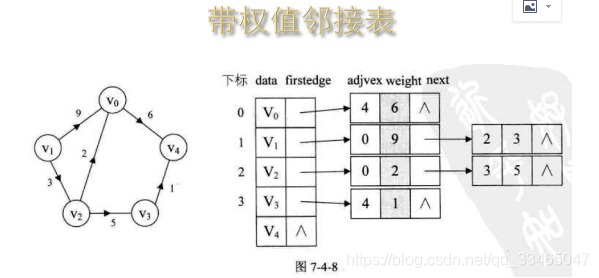
实例

class list_node:
def __init__(self):
self.val=0
self.next=None
head=[list_node()]*6 #声明一个节点类型的链表
newnode=list_node()
#图的数组声明
data=[[1,2],[2,1],[2,5],[5,2], \
[2,3],[3,2],[2,4],[4,2], \
[3,4],[4,3],[3,5],[5,3], \
[4,5],[5,4]]
print('图的邻接表内容:')
print('----------------------------------')
for i in range(1,6):
head[i].val=i #链表头head
head[i].next=None
print('顶点 %d =>' %i,end='') #把顶点值打印出来
ptr=head[i]
for j in range(14): #遍历图的数组
if data[j][0]==i: #如果节点值=i,加入节点到链表头
newnode.val=data[j][1] #声明新节点,值为终点值
newnode.next=None
while ptr!=None: #判断是否为链表的末尾
ptr=ptr.next
ptr=newnode #加入新节点
print('[%d] ' %newnode.val,end='') #打印相邻顶点
print()
图的邻接表内容:
----------------------------------
顶点 1 =>[2]
顶点 2 =>[1] [5] [3] [4]
顶点 3 =>[2] [4] [5]
顶点 4 =>[2] [3] [5]
顶点 5 =>[2] [3] [4]
图的性质:
- 性质1,若某图 的有度分别为TD(v1),TD(v2),TD(v3)...的顶点v1,v2,v3,vn。e条边或弧,则有 e = 1/2(TD(v1)+ ... + TD(v2))
- 性质2:一颗有n个顶点的生成树有且仅有n-1条边。










 本文详细介绍了图的两种主要存储方式:邻接矩阵和邻接表。通过具体实例,展示了无向图和有向图在不同存储结构下的表示方法,以及如何通过这些结构计算顶点的度和边的数量。
本文详细介绍了图的两种主要存储方式:邻接矩阵和邻接表。通过具体实例,展示了无向图和有向图在不同存储结构下的表示方法,以及如何通过这些结构计算顶点的度和边的数量。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








