局部图像描述子
1. Harris角点检测
1.1模型的目的
该角点检测模型主要是对窗口移动过程中像素的变化进行分析,如果窗口向任意方向移动都有很大的变化,则说明找到了角点。
1.2数学表达式
E(u,v)=∑x,yw(x,y)[I(x+u,y+v)−I(x,y)]2 E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2 E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
其中w(x,y)w(x,y)w(x,y)是感兴趣区域,也就是窗口函数。该窗口用于对像素的变化进行统计。E(u,v)E(u,v)E(u,v)表示窗口移动下得到的像素变化值。
I(x+u,y+v)−I(x,y)=uIx+vIy
I(x+u,y+v)-I(x,y)=uI_x+vI_y
I(x+u,y+v)−I(x,y)=uIx+vIy
E(u,v)=∑x,yw(x,y)[uIx+vIy]2 E(u,v)=\sum_{x,y}w(x,y)[uI_x+vI_y]^2 E(u,v)=x,y∑w(x,y)[uIx+vIy]2
[uIx+vIy]2=[uv][Ix2IxIyIxIyIy2][uv] [uI_x+vI_y]^2= \left[\begin{matrix} u&v \end{matrix}\right] \left[\begin{matrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2 \end{matrix}\right] \left[\begin{matrix} u\\v \end{matrix}\right] [uIx+vIy]2=[uv][Ix2IxIyIxIyIy2][uv]
E(u,v)=[uv][M][uv] E(u,v)= \left[\begin{matrix} u&v \end{matrix}\right] \left[\begin{matrix} M \end{matrix}\right] \left[\begin{matrix} u\\v \end{matrix}\right] E(u,v)=[uv][M][uv]
可以发现上式就是二次函数,MMM为特征矩阵。也是一个椭圆的表达式。
λ1,λ2\lambda_1,\lambda_2λ1,λ2是MMM的特征向量,表示在矩阵上表示为长短轴的大小。矩阵的其他部分决定了椭圆的旋转角度。
1.3公式的意义
M=[Ix2IxIyIxIyIy2] M = \left[\begin{matrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2 \end{matrix}\right] M=[Ix2IxIyIxIyIy2]
根据分析,Ix2I_x^2Ix2和Iy2I_y^2Iy2是图像在X,YX,YX,Y方向上的梯度大小,也决定了椭圆在长轴和短轴的大小。Harris角点检测通过对窗口内每个像素的xxx方向和yyy方向梯度进行统计分析得到结果。
-
对每一个像素点来说,都存在上述的结果。也可以明显的发现像下的角点,他的IxI_xIx和IyI_yIy都很大。
-
对整个窗口,如果整体呈现出来的结果和上述相似,也可以看做是角点了。
例如下面窗口。(参考博客:https://www.cnblogs.com/jiahenhe2/p/7930802.html)

他们的梯度分布情况为:
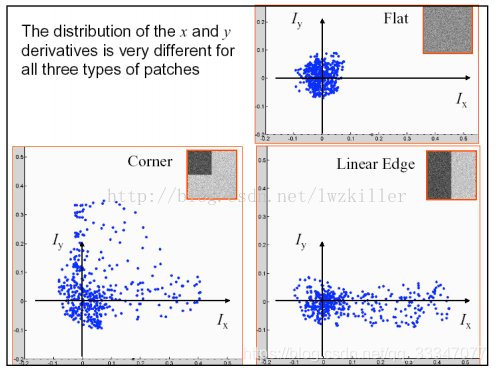
可以明显看到窗口中,如果存在竖着的分割线,那么他在xxx方向上存在一个极大的分割梯度。其他同理。
在进行特征值分析,需要将窗口内所有的像素点进行考虑。并拟合得到结果。
-
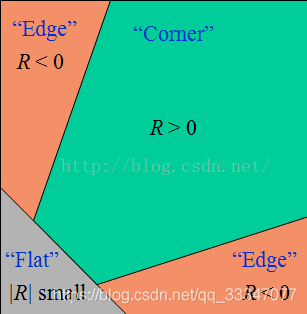
如果λ1\lambda_1λ1和λ2\lambda_2λ2是很大的正数,则表示为该点为角点
-
λ1\lambda_1λ1很大,λ2≈0\lambda_2\approx0λ2≈0则表示存在一个大边,区域内的平均MIM_IMI特征值不会变化太大
-
λ1≈λ2≈0\lambda_1\approx\lambda_2\approx0λ1≈λ2≈0则表示区域为空
1.4度量角点响应
R=detM−k(traceM)2 R=detM-k(traceM)^2 R=detM−k(traceM)2
detM=λ1λ2 detM=\lambda_1\lambda_2 detM=λ1λ2
traceM=λ1+λ2 traceM=\lambda_1+\lambda_2 traceM=λ1+λ2
kkk是常量,取值为0.04−0.060.04-0.060.04−0.06,参数仅仅是调节形状。
为了去除加权常数kkk,通常使用商数作为指示器:
det(MI)trace(MI)2
\dfrac{det(M_I)}{trace(M_I)^2}
trace(MI)2det(MI)
1.5 Harris计算流程
- 高斯函数的导数对原始图像进行卷积,得到图像在水平和垂直方向的导数IxI_xIx和IyI_yIy
- 计算梯度的外积(Ix2,Iy2,IxIy)(I_x^2,I_y^2,I_xI_y)(Ix2,Iy2,IxIy)
- 使用高斯函数对上述图像进行卷积滤波
- 计算角点的相应函数R值
- 计算的角点图像进行局部极大值抑制
1.6 python函数实现
from scipy.ndimage import filters
def compute_harris_response(im, sigma=3):
# 计算导数
imx = zeros(im.shape)
filters.gaussian_filter(im, (sigma, sigma), (0, 1), imx)
imy = zeros(im.shape)
filters.gaussian_filter(im, (sigma, sigma), (1, 0), imy)
# 计算Harris矩阵的分量
Wxx = filters.gaussian_filter(imx*imx, sigma)
Wxy = filters.gaussian_filter(imx*imy, sigma)
Wyy = filters.gaussian_filter(imy*imy, sigma)
# 计算特征值和迹
Wdet = Wxx*Wxx-Wxy**2
Wtr = Wxx + Wyy
return Wdet/Wtr
上述得到的是整个窗口得到一个响应图像。选取像素值高于阈值的点,加上角点之间间隔必须大于设定的最小距离的限制。
- 获取所有候选像素点,以角点响应值递减排序
- 删除距离已标记为角点位置过近的区域点
def get_harris_point(harrisim, min_dist=10, threshold=0.1):
# 高于阈值的像素点
corner_threshold = harrisim.max()*threshold
harrisim_t = (harrisim > corner_threshold) * 1
coords = array(harrisim_t.nonzero()).T
cadidate_values = [harrisim[c[0],[c[1]]] for c in coords]
#按照候选点排序
index = argsort(candidate_values)
allowed_locations = zeros(harrsim.shape)
allowed_locations[min_dist:-min_dist, min_dist:-mindist] = 1
# 按照min_distance原则,选择最佳harris点
filtered_coords = []
for i in index:
if allowed_locations[coords[i, 0], coords[i, 1]] == 1:
filtered_coords.append(coords[i])
allowed_locations[(coords[i, 0] - min_dist):(coords[i,0] + min_dist),
(coords[i, 1] - min_dist):(coords[i, 1]+min_dist)]=0
return filtered_coords




 本文深入解析Harris角点检测算法,从模型目的到数学表达,详细阐述如何通过分析像素变化来定位图像中的角点。包括特征矩阵的计算、特征值分析及角点响应度量,提供Python实现代码。
本文深入解析Harris角点检测算法,从模型目的到数学表达,详细阐述如何通过分析像素变化来定位图像中的角点。包括特征矩阵的计算、特征值分析及角点响应度量,提供Python实现代码。
















 5306
5306

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








