算法修炼——KNN（微进阶）

好了，又回来了。在进入本章之前，我们先来学一点东西：

超参数和模型参数：

那么我们应该怎样去寻找好的超参数呢？

一般来说有三个方法：领域知识、经验数值、实验搜索。

我们的knn也有两个很重要的超参数：1、k值的选取 。  2、距离的权重。

接下来让我们寻找最好的k值：

 首先我本次使用的是digits数字集：

digits = datasets.load_digits()
X = digits.data
y = digits.target

# 然后调用sklearn的分割函数，分割数据集（将数据集分为训练集和测试集）。

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=666)

 

from sklearn.neighbors import KNeighborsClassifier

# 思路，遍历1-11 ，分别拿每一个k去调用knn算法，取出分值最高的那个k
best_k = -1
best_score = 0.0
for i in range(1,11):
    clf_knn1 = KNeighborsClassifier(n_neighbors=i)
    clf_knn1.fit(X_train,y_train)
    score = clf_knn1.score(X_test,y_test)
    if score > best_score:
        best_k = i
        best_score = score
# 如果best_k为10，则需要测试10以后的数。
print("best_k=",best_k)
print("best_score",best_score)

很明显，我们找到了最好的k值为4，这个时候我们的knn算法的准确度达到了99.1%。

 

大家应该能发现，上一章的knn算法有一个很明显的不足，那就是没有考虑距离的权重。我们来看一张图：

如果按照我们原来的那种算法，最后的结果就是目标点是蓝色，但是考虑权重以后目标点应该是红的。（般情况下使用距离的导数作为权证），而且，考虑权重可以帮助我们解决平票的问题。

接下来，让我们用代码验证一下考虑距离与不考虑距离的区别：

# 思路，遍历1-11 ，分别拿每一个k去调用knn算法，取出分值最高的那个k
best_method = ""
best_k = -1
best_score = 0.0
for m in ["uniform","distance"]:
    for i in range(1,11):
        clf_knn1 = KNeighborsClassifier(n_neighbors=i,weights=m)
        clf_knn1.fit(X_train,y_train)
        score = clf_knn1.score(X_test,y_test)
        if score > best_score:
            best_k = i
            best_score = score
            best_method = m
# 如果best_k为10，则需要测试10以后的数。
print("best_k=",best_k)
print("best_score=",best_score)
print("best_method=",best_method)

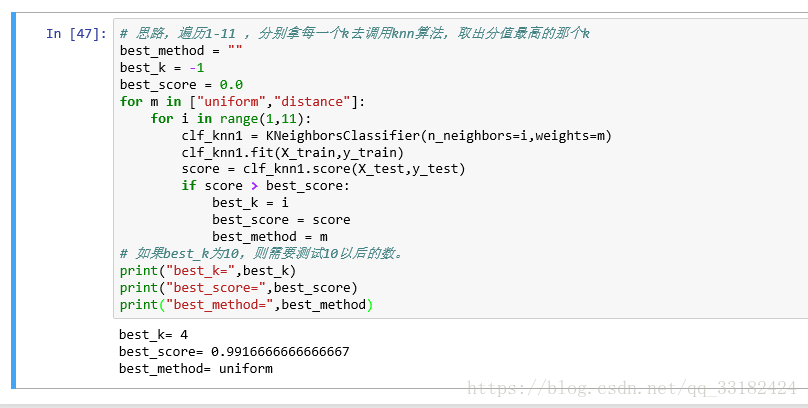
由结果我们发现，对于我们的数字集还是不考虑距离权重的结果更好，但这只是个例，接下来我们还是引入距离的概念：

那么我们既然要考虑距离，那么我们需要考虑的是什么距离？

1、欧拉距离

2、曼哈顿距离：

什么是曼哈顿距离，就是X1，X2两个样本在每个维度上的差值的和。

 我们可以发现欧拉距离和曼哈顿距离在数学形式上具有一定的一致性：

最后我们可以推广出一个公式，数学上称这个距离为：明克夫斯基距离。

然后，我们就获得了一个新的超参数：p

接下来，让我用代码搜索明可夫斯基距离相应的p：

# 思路，遍历1-11 ，分别拿每一个k去调用knn算法，取出分值最高的那个k
best_p = -1
best_k = -1
best_score = 0.0
for i in range(1,11):
    for p in range(1,6):
        clf_knn1 = KNeighborsClassifier(n_neighbors=i,weights="distance",p=p)
        clf_knn1.fit(X_train,y_train)
        score = clf_knn1.score(X_test,y_test)
        if score > best_score:
            best_k = i
            best_score = score
            best_p = p
# 如果best_k为10，则需要测试10以后的数。
print("best_k=",best_k)
print("best_score",best_score)
print("best_p=",best_p)

关于网格搜索，归一化问题，下一章再做介绍。

刚刚开始学习，有不对的地方，还望多多指正。