【数据结构算法】卡塔兰数的几个算法应用问题

卡塔兰数

至于什么是卡塔兰数自己去这里了解哈
这里给出算法迭代公式
``h(n)=(4n-2)/(n+1)*h(n-1) (n>=1) h(0)=1

可以直接使用的算法题

使用问题的场景：n个0和n个1组成一个2n位的2进制数，要求从左到右扫描时，1的累计数始终都小于等于0的累计数，求满足条件的数有多少？

下面的场景

题1 所有的出栈次数

假设 n 个数依次进栈，中间运允许出栈，求所有的可能出栈次数

题2 找零钱

有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票， 剧院无其它钞票，
问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？

题3 三角网络

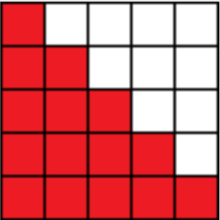
小兔的叔叔从外面旅游回来给她带来了一个礼物，小兔高兴地跑回自己的房间，拆开一看是一个棋盘，小兔有所失望。不过没过几天发现了棋盘的好玩之处。从起点(0，0)走到终点(n,n)的最短路径数是C(2n,n),现在小兔又想如果不穿越对角线(但可接触对角线上的格点)，这样的路径数有多少?

题3 括号排列

• 矩阵连乘：共有（n+1）项，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？
• 有n对括号，可以并列或嵌套排列，共有多少种情况？

题4 球盒问题

• 球分两种颜色，黑色和白色分别各有n只，盒子数量和球的个数相同，每个盒子里面只能放一只球，并且必须满足如下限制,即每一个白球必须和一只黑球配对（白球在黑球前，允许嵌套）

其他

• (1).将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域的方法数?
• (2).有N个节点的二叉树共有多少种情形？
• (3).在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

参考

来自这里