批归一化:通过减小内部协方差平移(internal covariate shift)加速深层网络训练
论文地址:https://arxiv.org/abs/1502.03167
目录
批归一化:通过减小内部协方差平移(internal covariate shift)加速深层网络训练
3.1训练以及推理BNN(Batch Normalized Network)
-
介绍
SGD被证明是优化的高效方法,优化了参数,并且最小化误差。
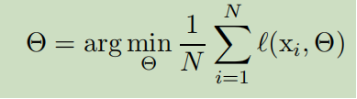
其中x1-xn是样本,mini-batch被用作接近损失函数的梯度,通过计算
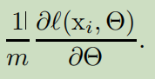
其中m代表mini-batch。使用mini-batch而不是每次一个样本,有以下好处:首先,一个mini-batch内损失函数的梯度是对整个训练集梯度的估计,当batch size增加时,梯度的质量也会增加。其次,计算一个batch比计算m次单独的样本更有效,因为并行计算的原因。
虽然随机梯度是简单高效的,但是需要对网络超参数的精细调制。因为网络层需要不断的更新,层输入的分布带来了困难。协方差的
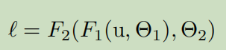
F1和F2是任意的变换,为了减少误差而被学习。可以看作是如果输入为被喂入子网络,例如,一个梯度下降步骤
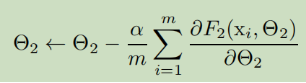
是恰好相等的,对于一个单独的输入为x的网络F2(其中α为学习率,m是批尺寸)。这样下来,网络(包括子网络)的输入分布就是固定的了。考虑一个sigmoid激活函数,z=g(Wu+b),u是层输入,其中
![]() 。
。
当|x|增加,g’(x)趋于0.这意味着x=Wu+b的所有维度除了特别小的绝对值,梯度减小到u会发生消失,而神经网络会训练的特别慢。然而,因为x被W,b 和先前层所有参数所影响。对这些参数的改变会把x的很多维度变成非线性饱和状态,并且减慢了收敛。这种效应被放大,当网络深度增大。实际上,饱和问题和网络梯度消失问题是由线性整流网络和精细的初始化,以及小的学习率所解决。
-
减小内部协方差平移
漂白(whitening)输入,比如线性的变换使平均值为0,单位化方差,去相关 ,会使网络收敛更快。可以通过考虑漂白激活每个训练step的激活函数或者一定的间隔,要么直接改变网络,或者改变优化函数的算法。批归一化可以写成:
![]()
这里x是某一层的输入,是一系列的输入。对于反向传播,需要计算Jaccobians:

在这个框架下,漂白层输入,代价昂贵,而且需要计算协方差矩阵![]()
。这启示我们去找到一种替代方法。
-
通过Mini-Batch数据的归一化
因为对每一层的输入漂白十分昂贵,我们作两点简化。第一,对标量特征单独归一化,使得它平均值为0,方差为1.对于一个d维层输入x=(x1......xd)。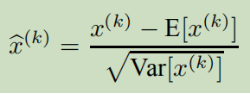
E表示期望值,而Var表示方差,是在整个训练集得到的。这种归一化加速了收敛,即使特征没有去相关。
注意,归一化每一层的输入会改变层的表示。例如,归一化函数sigmoid限制它在非线性区。为了解决这个问题,我们确保了插入到网络的变换能够表示特征变换。为了实现之,引入了一对参量,变换(scale)和平移(shift)了标准化的值。
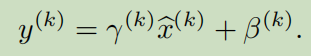
这些参数和原始模型一起被学习,保留了网络的表示能力。设置![]() ,
,![]() ,可以恢复原始的激活函数,优化效果最好。
,可以恢复原始的激活函数,优化效果最好。
对于使用SGD优化函数 ,使用整个训练集来归一化激活函数不切实际。因此,产生了第二个简化。因为在随机(stochastic)梯度训练使用mini-batch,每一个mini-batch产生了对平均值和方差的估计。 这样,归一化数据可以完全参与到梯度的反向传播过程。

其中是一个常数用于增加稳定性,避免方差为0。参数γ和β是网络学习的参数。
BN取决于训练的样本以及在mini-batch中的其他样本,y也被传递到网络其他层。在训练过程中,我们需要反向传播误差l通过这种变换,并且计算BN变换的参数。使用链式法则:
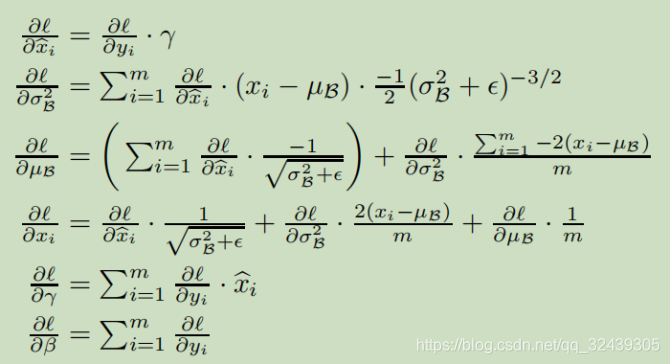
BN变换是一种可微的变换,引入了归一化的激活函数到网络中。而且,学习到的仿射变换使得BN变换能够表示特征变换并且保留网络的容量。
3.1训练以及推理BNN(Batch Normalized Network)
我们需要输出唯一地由输入决定,因此采用:
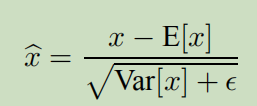
我们使用无偏置的方差估计。(为什么是m-1).使用移动平均,我们可以记录模型训练的准确率。一下是训练BNN的一般步骤:


这些步骤证明BN网络的参数是可微的,训练集得到的γ和β可以直接运用到测试集。
- 对仿射变换的理解:
例如我们对参数W进行缩放得到aW。对于缩放前的值Wu,设其均值为u1,对于缩放后的值,设其均值为u2:
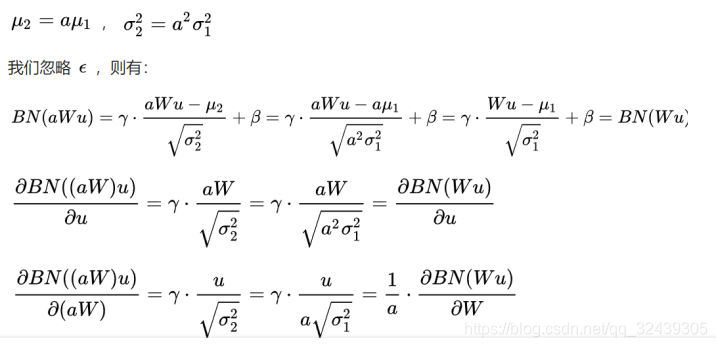
经过BN操作,权重的缩放值消失,对第二个式子。当权重值越大,a越大,1/a越小,意味着权重W反而越小,这样BN就不会依赖输入参数的scale,使得参数 更新后处在更加稳定的状态。我们可以使用更大的学习率,加快收敛。
算法2:训练一个BNN
3.2批归一化的卷积网络
这里,我们关注一个包含一个仿射变换,接着是一个逐元素的非线性:
![]()
这里W,b是被学习的模型参数,g(·)是非线性,如ReLU或者sigmoid。这个公式即包括全连接层也包括卷积层,我们在非线性层前立即加入BN,通过归一化x=Wu+b.我们也可以归一化层输入u,但因为u有可能是另一个非线性。相反地,Wu+b更有可能有一个对称的非稀疏的分布。
注意b可以被忽略,因为它的效应可以被后续的平均减法所抵消,因此z=g(Wu+b)可以被z=g(BN(Wu))替代。每一层的γ和β都是独立的。
对于卷积层,我们需要卷积层也遵守BN,为了实现这个,我们共同地归一化所有的激活函数在一个mini-batch。令B为一系列特征图的取值(feature map)在mini-batch或者空间位置,所有对于m大小的mini-batch,特征图尺寸为p*q ,我们使用有效的m’=|B|=m·pq,每个特征图而不是每个激活函数学习到一对γ和β。所以在推理阶段,BN变换使用了同样的线性变换在给定的特征图。
3.3 BN使得学习率更高
采用BN,反向传播不会受参量大小的影响。对于标量a。
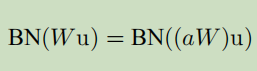
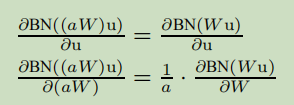
这些尺寸并不会影响Jacobian,结果是梯度传播。而且,大的权重带来了更小的梯度,BN保证了参数稳定。
3.4 BN正则化了模型
BN有利于模型的泛化。而Dropout通常用于减小过拟合,。BN可以减少dropout的使用。
-
测试
基于MNIST和ImageNet
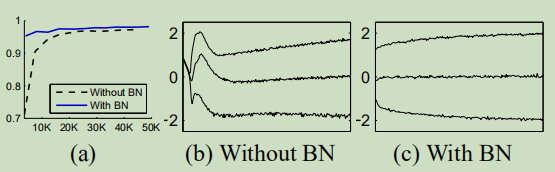

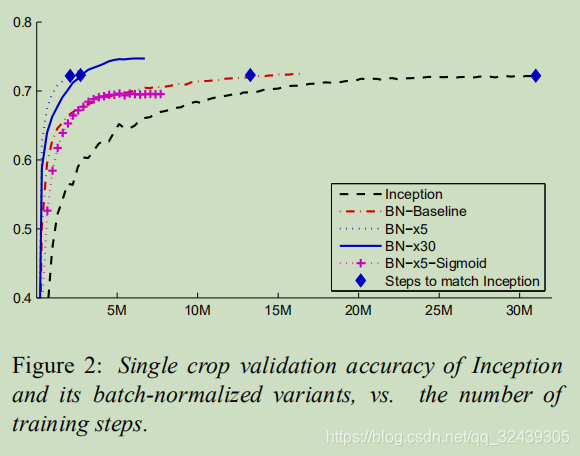
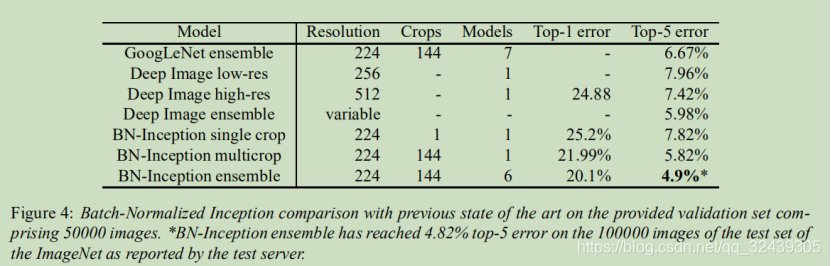








 本文探讨了批归一化(Batch Normalization)如何通过减小内部协方差平移,加速深层网络的训练过程。介绍了批归一化的基本原理,如何在训练和推理中应用,以及其在卷积网络中的作用。此外,文章还讨论了批归一化如何允许使用更高的学习率,正则化模型,减少过拟合。
本文探讨了批归一化(Batch Normalization)如何通过减小内部协方差平移,加速深层网络的训练过程。介绍了批归一化的基本原理,如何在训练和推理中应用,以及其在卷积网络中的作用。此外,文章还讨论了批归一化如何允许使用更高的学习率,正则化模型,减少过拟合。
















 85
85

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








