Dijkstra最短路径算法的java实现

迪杰斯特拉算法

迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

如下图：令Graph =（V，E）为一个带权无向图。Graph中若有两个相邻的节点i和j。Graph[i][j]为节点i到节点j的权值，在本算法可以理解为距离。每个节点都有一个值mindist[i]表示其从起点到它的某条路的最短距离。

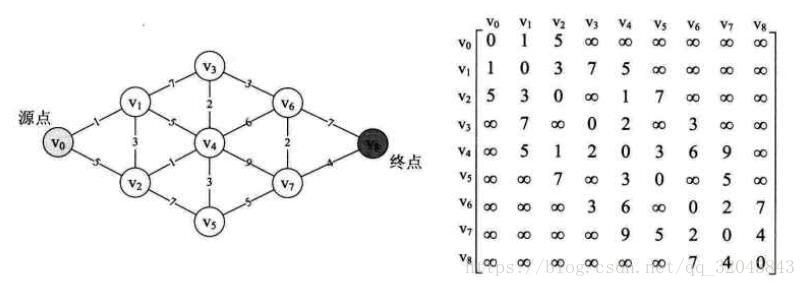
下面是从网络上找到比较简洁的Java代码（笔者只是做个搬运工，如有侵权请联系笔者删除）：

/**
 * Dijkstra最短路径。
 * 既图中“节点vs”到其它各个节点的最短路径。
 * @param vs 起始节点
 * @param Graph 图
 */

public class Dijkstra 
{
	private static int N = 1000;
	private static int[][] Graph = {
	    { 0, 1, 5, N, N, N, N, N, N },
            { 1, 0, 3, 7, 5, N, N, N, N },
            { 5, 3, 0, N, 1, 7, N, N, N },
            { N, 7, N, 0, 2, N, 3, N, N },
            { N, 5, 1, 2, 0, 3, 6, 9, N },
            { N, N, 7, N, 3, 0, N, 5, N },
            { N, N, N, 3, 6, N, 0, 2, 7 },
            { N, N, N, N, 9, 5, 2, 0, 4 },
            { N, N, N, N, N, N, 7, 4, 0 }
	};
	
	public static void main(String[] args)
	{
		dijkstra(0, Graph);
	}
	
	public static void dijkstra(int vs, int[][] Graph)
	{
		int NUM = Graph[0].length;
		System.out.println(NUM);
		//前驱节点数组
		int[] prenode = new int[NUM];
		//最短距离数组
		int[] mindist = new int[NUM];
		//该节点是否已经找到最短路径
		boolean[] find = new boolean[NUM];
		
		int vnear = 0;
		
		for(int i = 0; i < mindist.length; i++)
		{
			prenode[i] = i;
			mindist[i] = Graph[vs][i];
			find[i] = false;
		}
		
		find[vs] = true;
		
		System.out.println(Graph.length);		
		for(int v = 1; v < Graph.length; v++)
		{
			//每次循环求得距离vs最近的节点vnear和最短距离min
			int min = N;
			for(int j = 0; j < Graph.length; j++)
			{
				if(!find[j] && mindist[j] < min)
				{
					min = mindist[j];
					vnear = j;
				}
			}
			find[vnear] = true;
			
			//根据vnear修正vs到其他所有节点的前驱节点距离
			for(int k = 0; k < Graph.length; k++)
			{
				if(!find[k] && (min + Graph[vnear][k]) < mindist[k])
				{
					prenode[k] = vnear;
					mindist[k] = min + Graph[vnear][k];
				}
			}			
		}
		
		for(int i = 0; i < NUM; i++)
			System.out.println("v" + vs + "...v" + prenode[i] + "->v" + i + ", s=" + mindist[i]);
	}
}