泊松分布 -- 二项分布的拟合

                                                 泊松分布

首先浅谈二项分布，设实验 E 服从 （0-1）分布，则每次 E 的实验称之为 伯努利实验  ，二项分布就是 多重的 独立的 伯努利实验。设进行 n 次伯努利实验，每次发生的概率为 p，则发生 k 次的概率 P{X = k} 为

                                     

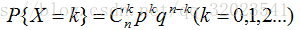
现在我们设想一个特殊的情况，假设事件每次发生的概率 p 很小，并且重复实验的次数 n 比较大，那么当这种情况的二项分布时，有（不好写公式，用草稿代替）

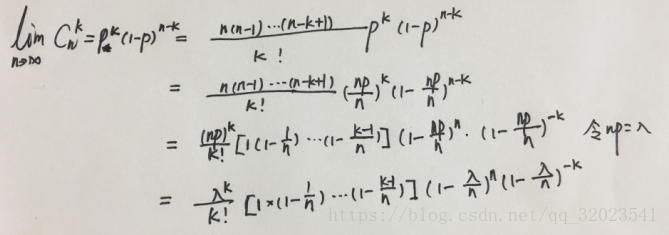
继续推导

 

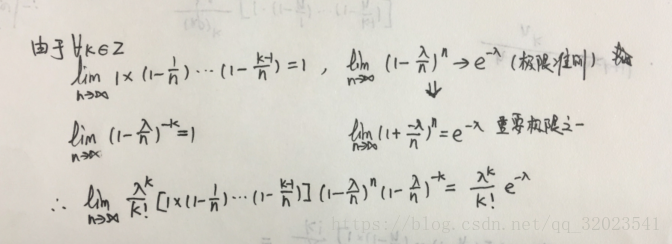
上述中的公式表明，当 n 重伯努利实验的 n 足够大，并且每次伯努利实验的概率 p 发生比较小时，发生次数 k  的概率 P{X=k}

可以用下列公式表示（其中 ）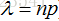

   

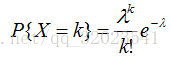
这就是 泊松分布 公式，也就是当二项式分布满足 p 很小，而 n 很大时，我们可以用 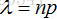 的泊松分布拟合，或者说 X 服从 参数为 lambda 的泊松分布，简称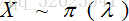  

 

可以证明：

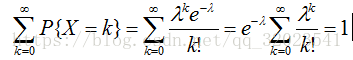
备注：以上公式的证明可用麦克劳林展开式

 

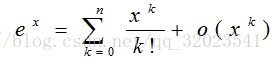
即