第四课 牛顿法

一 牛顿法

目标：对于函数,找到一个，使得

步骤：

1)       给出一个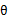的初始值

2)       对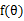求导，求导数为0时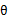的值（就是求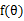切线与x轴交点）

3)       重复步骤2

 

算法迭代过程如下图所示：

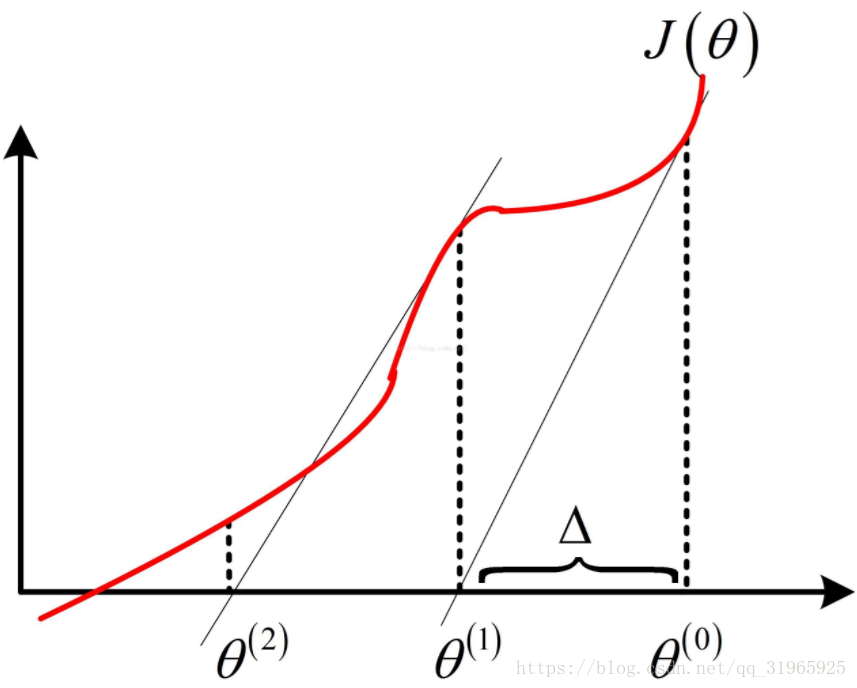
其中为初始值，为第一次迭代的值，为第二次迭代的结果。

迭代的目的就是使最大

所以

 

应用于Logistic回归：

求对数似然的最大值，即求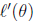为0时的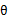，根据上述推论，更新规则如下：

 

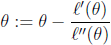
牛顿方法的收敛速度：二次收敛。每次迭代使解的有效数字的数目加倍：假设当前误差是0.1，一次迭代后，误差为0.001，再一次迭代，误差为0.0000001。该性质当解距离最优质的足够近才会发现。

 

牛顿方法的一般化

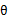是一个向量而不是一个数字，一般化的公式为：

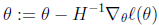
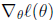是目标函数的梯度，H为Hessian矩阵，规模是n*n，n为特征的数量，它的每个元素表示一个二阶导数：

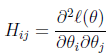
上述公式的意义就是，用一个一阶导数的向量乘以一个二阶导数矩阵的逆

优点：若特征数和样本数合理，牛顿方法的迭代次数比梯度上升要少得多

缺点：每次迭代都要重新计算Hessian矩阵，如果特征很多，则H矩阵计算代价很大

 

二 指数分布族

指数分布族的定义：

若一类概率分布可以写成如下形式，那么它就属于指数分布族：

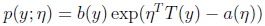
其中η - 自然参数，通常是一个实数

T(y) – 充分统计量，通常，T(y)=y，实际上是一个概率分布的充分统计量（统计学知识）

对于给定的a，b，T三个函数，上式定义了一个以η为参数的概率分布集合，即改变η可以得到不同的概率分布。

 

证明伯努利分布是指数分布族：

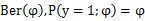
可知：

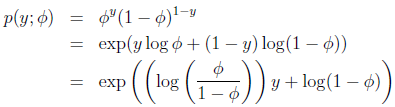
由上式可见，η=log(φ/(1-φ))，可解出：φ=1/(1+exp(-η))，发现得到logistic函数（之后讨论其原因），则：

 

 

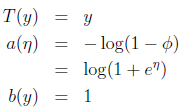
证明高斯分布是指数分布族：

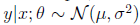，设方差为1（方差并不影响结果，仅仅是变量y的比例因子）

这种情况下高斯密度函数为：

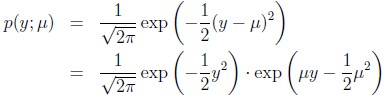
可得：

 

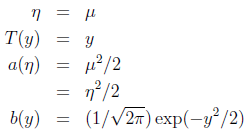
*指数分布族包括：高斯分布（正态分布），多元正态分布；伯努利分布（01问题建模），多项式分布（对k个结果的事件建模）；泊松分布（对计数过程建模）；伽马分布，指数分布（对实数的间隔问题建模）；β分布，Dirichlet分布（对小数建模）；Wishart分布（协方差矩阵的分布）