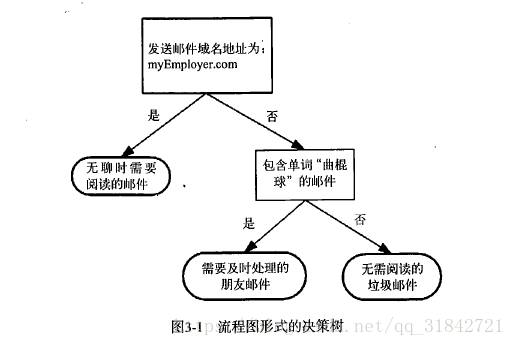
1.决策树的特点
决策树是最常用的数据挖掘算法,可以方便的处理分类问题,概念简单,容易理解,而knn算法无法给出数据的内在含义(只是相似度的计算,不直观)。决策树组织的数据形式非常容易理解,也非常直观。决策树由决策结点、分支和叶子组成。决策树中最上面的结点为根结点,每个分支是一个新的决策结点,或者是树的叶子。每个决策结点代表一个问题或决策,通常对应于待分类对象的属性。每一个叶子结点代表一种可能的分类结果。沿决策树从上到下遍历的过程中,在每个结点都会遇到一个测试,对每个结点上问题的不同的测试输出导致不同的分支,最后会到达一个叶子结点,这个过程就是利用决策树进行分类的过程,利用若干个变量来判断所属的类别。
引自《机器学习实战》:

2.决策树
使用香农熵计算数据的无序程度,通过选取最佳划分特征维度进行子集划分,递归记录划分的特征维度及其取值的嵌套列表
1)decisiontree.py
from numpy import * import operator from math import log import pickle ''' 创建测试数据集 ''' def create_dataset(): # 注意这里的构造函数,array一般必须是相同类型的,这里不能采用这种初始化方式 # dataset=array([[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]) dataset = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] labels = ['no surfacing', 'flippers'] return dataset, labels ''' 读取指定目录下的文件形成数据集 隐形眼镜数据集是非常著名的数据集,它包含了很多患者眼部状况的观察条件以及医生推荐的隐形眼镜类型。 隐形眼镜类型包括硬材质(hard)、软材质(soft)以及不适合佩戴隐形眼镜(no lenses) * 特征有四个:age(年龄)、prescript(症状)、astigmatic(是否散光)、tearRate(眼泪数量) * 隐形眼镜类别有三类(最后一列):硬材质(hard)、软材质(soft)、不适合佩戴隐形眼镜(no lenses) ''' def readData(filepath): dataset=[] with open(filepath,'r') as fd: lines=fd.readlines() for str in lines: str=str.strip() dataset.append(str.split('\t')) labels=['age','prescript','astigmatic','tearRate'] return dataset,labels ''' 计算香农熵sum(-p log2p) p:出现的次数除以总次数 ''' def cacuShannonEnt(dataset): # 计算总次数 totoalCount = len(dataset) # 计算标签出现的次数 labelCount = {} for row in dataset: if row[-1] not in labelCount: labelCount[row[-1]] = 0 labelCount[row[-1]] += 1 shannoent = 0.0 for value in labelCount.values(): p = value / totoalCount p = p * log(p, 2) shannoent -= p return shannoent ''' 获取指定测量维度等于指定值的元素列表 ''' def splitDatatSet(dataset, axis, value): retDataSet = [] for data in dataset: # 指定维度的指定值的元素 if data[axis] == value: retData = data[:axis] retData.extend(data[axis + 1:]) retDataSet.append(retData) return retDataSet ''' 选择最好的划分,注意输入数据集为列表形式,最后一列为标签值,其他列是特征维度 ''' def chooseBestFeatureToSpilt(dataset): # 计算特征维度的个数 featureCount = len(dataset[0]) - 1 #计算基础香农熵 baseShannoEnt=cacuShannonEnt(dataset) bestShannoEnt=0.0 beatI=0 # 循环每个特征维度 for i in range(featureCount): #获取指定i列维度所有值列表 featureValueList=[ row1[i] for row1 in dataset] #去重 featureValueSet=set(featureValueList) #对于本次划分计算所有可能值综合香农熵 #按照i维度,然后该维度的不同取值,可以得到不同的集合划分,对这些集合计算香农熵并乘以其所占的权重比,最后求和 #这样得出的就是本次划分的信息增益,然后选择信息增益最好的就是最好的划分。featureShannoEnt越小越好,infoShannoEnt越大越好。 #数据越规整,香农熵越小, 反之,香农熵越大 featureShannoEnt=0.0 for featureValue in featureValueSet: #得到划分集合 splitDataSet=splitDatatSet(dataset,i,featureValue) #在本次集合划分结果基础上计算香农熵 featureShannoEnt+=(cacuShannonEnt(splitDataSet)*(len(splitDataSet)/float(len(dataset)))) infoShannoEnt=baseShannoEnt-featureShannoEnt if infoShannoEnt>bestShannoEnt: bestShannoEnt=infoShannoEnt beatI=i return beatI ''' 选取出现次数最多的分类标签 ''' def majorityCnt(classList): classDict={} #统计出现的次数 for vote in classList: if vote in classDict: classDict[vote]+=1 else: classDict[vote]=1 print(classDict.items()) #按照出现的次数逆序排序 sortClassDict=sorted(classDict.items(),key=operator.itemgetter(1),reverse=True) print('sortClassDict ',sortClassDict) return sortClassDict[0][0] ''' 构造决策树 构造方法: 使用香农熵计算数据的无序程度,根据香农熵可以计算出最优的划分特征, 根据最优划分特征及其不重复的值,可以获取到原数据集的多个子集, 判断子集是否达到临界条件,1.集合中的元素都是同一种分类的的,比如[1,yes][2,yes],已经产生了分类 2,当前集合已经没有分类的维度,且不是同一种分类,比如[yes][yes][no],这种返回出现成次数最多的, 重复此过程,可以递归创建决策树,沿途记录最优判断特征维度及其值 输入: 1)数据集,满足多个特征维度+一个分类 2)对应特征维度的标签值 输出: 最优特征维度及其值的嵌套字典,字典记录了一条搜索路径,叶子结点记录了这条搜索路径的最终结构, key:为特征维度,value:搜索结果或者子搜索路径 注意: 1)啥时候需要新生成数据结构,啥时候需要传递数据结构的引用 2)递归的边界条件 ''' def createTree(dataset,labels): #递归临界条件,树的孩子结点 #取最后一列分类 classList=[row[-1] for row in dataset] #比较第一个元素类型的个数和总个数是否相等,相等说明是同一种类型 if classList.count(classList[0]) == len(classList) : #返回当前分类 return classList[0] #判断是否已经没有分类维度了,只包含分类那一列了,返回出现次数最多的分类 if len(dataset[0]) == 1: return majorityCnt(classList) #获取当前数据集合和标签列表的最优特征维度 bestFeatureId=chooseBestFeatureToSpilt(dataset) #最优特征维度对应的标签值 bestFeatureLabel=labels[bestFeatureId] #获取最优特征维度的不重复的特征值 featureValuesList=[row[bestFeatureId] for row in dataset] featureValues=set(featureValuesList) #删除已经使用的特征值对应的标签值,获取子集,重置递归数据 del(labels[bestFeatureId]) #遍历特征值,获取特征维度和维度值的对应子集,递归创建决策树子节点 #使用嵌套字典记录指定最优特征维度标签和最优特征维度值,对应的决策分类值 tree1={bestFeatureLabel:{}} for featureValue in featureValues: #这里复制了类标签,因为要递归处理多个值,需要保持不同递归函数之间仅通过参数和返回值沟通, # 输出参数,对于不同递归函数,有些需要不变,这里通过复制,保持初始数据不受其他递归函数的影响 subLables=labels[:] #注意,这里会新生成一个集合,原来集合不变 subDataSet=splitDatatSet(dataset,axis=bestFeatureId,value=featureValue) tree1[bestFeatureLabel][featureValue]=createTree(subDataSet,subLables) return tree1 ''' 使用决策树进行分类,不要求输入的标签一定与决策树构建的最优特征维度保持一致,但取值需要与原始创建的输入保持一致,不要求顺序 输入: tree:决策树 labels:标签 indx:测量数据 ''' def classify(tree,labels,indx): #取第一个属性值 firstKey=list(tree.keys())[0] #取第二个字典,这里可能是单个值 secondDict=tree[firstKey] #遍历第二个字典 for key,value in secondDict.items(): #获取决策树的特征维度对应的标签下标,进而找到测量数据这个维度的输入值 #根据值递归走不同的树的分支 if indx[labels.index(firstKey)]==key : if type(value).__name__=='dict' : classResult=classify(value,labels,indx) else: classResult=value return classResult def saveTree(tree,filepath): with open(filepath,'wb') as fd: pickle.dump(tree,fd) def loadTree(filepath): with open(filepath,'rb') as fd: return pickle.load(fd) #dataset, lables = create_dataset() #print(dataset, lables) #shannoent = cacuShannonEnt(dataset) #print(shannoent) # dataset[0][-1]='no' # shannoent=cacuShannonEnt(dataset) # print(shannoent) #print(splitDatatSet(dataset, 0, 1)) #dataset = [[1, 1, 'yes'], [1, 1, 'maybe'], [1, 0, 'maybe1'], [0, 1, 'maybe2'], [0, 1, 'no']] #全是yes 0,4个yes 1个no 0.7219280948873623, 3个yes 2个no 0.9709505944546686 ,1个yes 1个maybe 3个no 1.3709505944546687 #2个yes 1个maybe 3个no 1.5219280948873621 全部都不一样!!!2.321928094887362 #数据越规整(该维度作为标准,区分不同分类的效果更好),香农熵越小, 反之,香农熵越大 #print(cacuShannonEnt(dataset)) #tree=createTree(dataset,lables) #print(tree)
绘制决策树
2)treeplotter.py
import matplotlib.pyplot as plt import decisiontree as dtree ''' 绘制决策树 ''' #定义格式 #节点格式 decisionNode=dict(boxstyle='sawtooth',fc='0.8') #叶节点格式 leafNode=dict(boxstyle='round4',fc='0.8') #箭头格式 arrow_args=dict(arrowstyle='<-') def createPlot(inTree): fig = plt.figure('决策树') fig.clf() axprops = dict(xticks=[], yticks=[])# 定义横纵坐标轴,无内容 #createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # 绘制图像,无边框,无坐标轴 createPlot.ax1 = plt.subplot(111, frameon=False) plotTree.totalW = float(getNumLeafs(inTree)) #全局变量宽度 = 叶子数 plotTree.totalD = float(getTreeDepth(inTree)) #全局变量高度 = 深度 #图形的大小是0-1 ,0-1 plotTree.xOff = -0.5/plotTree.totalW; #例如绘制3个叶子结点,坐标应为1/3,2/3,3/3 #但这样会使整个图形偏右因此初始的,将x值向左移一点。 plotTree.yOff = 1.0; plotTree(inTree, (0.5,1.0), '') plt.show() def plotTree(myTree, parentPt, nodeTxt): numLeafs = getNumLeafs(myTree) #当前树的叶子数 depth = getTreeDepth(myTree) #没有用到这个变量 firstStr = list(myTree.keys())[0] #cntrPt文本中心点 parentPt 指向文本中心的点 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) plotMidText(cntrPt, parentPt, nodeTxt) #画分支上的键 plotNode(firstStr, cntrPt, parentPt, decisionNode) secondDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD #从上往下画 for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict':#如果是字典则是一个判断(内部)结点 plotTree(secondDict[key],cntrPt,str(key)) else: #打印叶子结点 plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) ''' 实际绘制函数 nodeTxt:节点文本 centerPl:节点文本位置 parentPl:线的开始位置 nodetype:节点类型 ''' def plotNode(nodeTxt,centerPl,parentPl,nodeType): createPlot.ax1.annotate(nodeTxt,xy=parentPl,xycoords='axes fraction',xytext=centerPl, textcoords='axes fraction',va='center',ha='center',bbox=nodeType,arrowprops=arrow_args) ''' 获取叶子节点的个数 ''' def getNumLeafs(tree): #如果是遍历到叶子节点 if type(tree).__name__!='dict' : return 1 leafNodeCount=0 for value in tree.values(): leafNodeCount+=getNumLeafs(value) return leafNodeCount ''' 获取树的深度 ''' def getTreeDepth2(tree): # 如果是遍历到叶子节点,只有一个节点,算1 if type(tree).__name__ != 'dict': return 1 maxTreeDepth = 0 #递归获取所有子节点的深度,取最大的那个 for value in tree.values(): childTreeDepth=getTreeDepth(value) if childTreeDepth > maxTreeDepth : maxTreeDepth=childTreeDepth keysList=[key for key in tree.keys()] #这里需要区分下{'flippers': {0: 'no', 1: 'yes'}} 和{0: 'no', 1: 'yes'},虽然都是字典类型,前面这种就能算一个节点 #所以可以在得到所有子节点的最大深度+1 if type(list(tree.keys())[0]).__name__=='str': return maxTreeDepth+1 else: return maxTreeDepth def getTreeDepth(myTree): maxDepth = 0 firstStr = list(myTree.keys())[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict': thisDepth = 1 + getTreeDepth(secondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth #createPlot() dataset,labels = dtree.create_dataset() print(dataset,labels) #注意这里会改变输入数据的值,因为传入的是引用,del(labels[bestFeatureId]),这里应该传入list(x) tree=dtree.createTree(dataset,list(labels)) print(tree) #print(getNumLeafs(tree)) #print(getTreeDepth(tree)) print('不能露出水面且脚上有蹼,是否为鱼?') classResult=dtree.classify(tree,labels,[1,1]) print(classResult) print('可以露出水面且脚上有蹼,是否为鱼?') classResult=dtree.classify(tree,labels,[0,1]) print(classResult) #绘制决策树 #createPlot(tree) #winows文件路径需要用'//',不能用'\' path='D://software//python//output//tree.txt' dtree.saveTree(tree,path) print(dtree.loadTree(path))
3.绘制效果
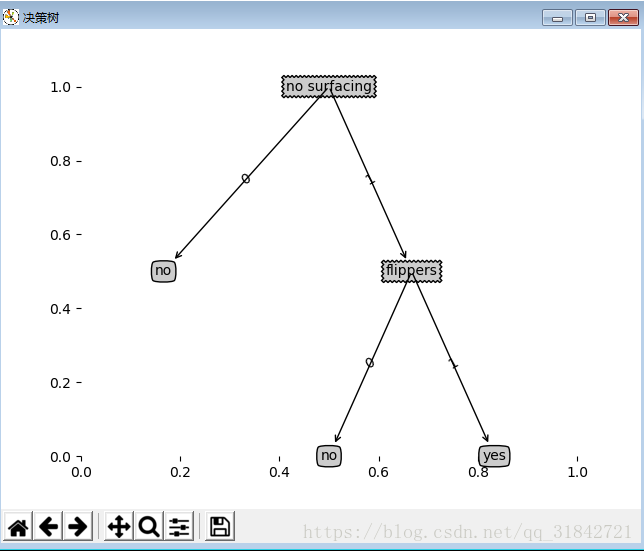
决策树分类判断:

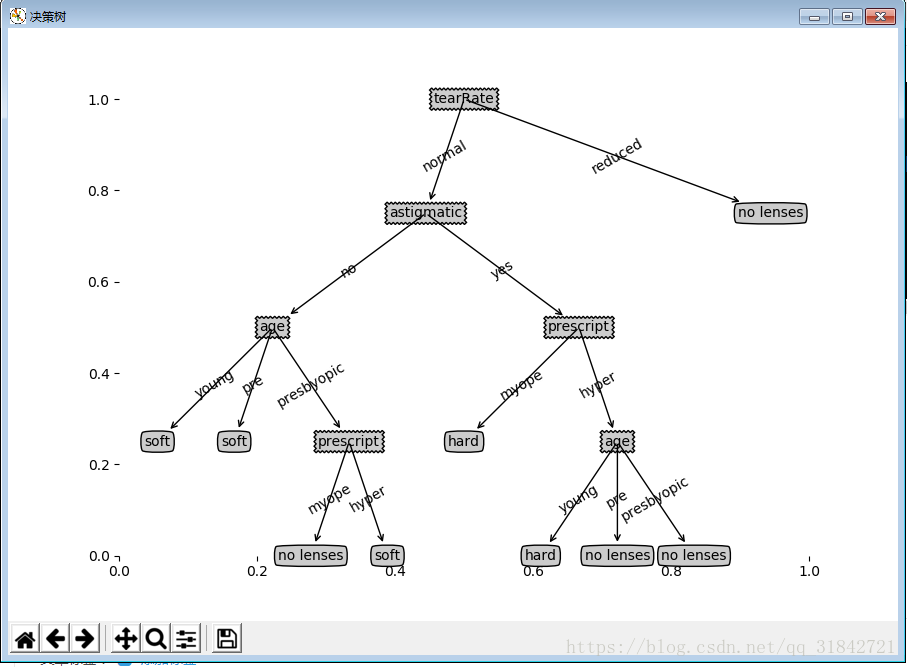
4.决策树的应用:预测眼镜的类型
import decisiontree as dtree import treePlotter as tplt path='\machinelearninginaction\Ch03\lenses.txt' dataset,labels=dtree.readData(path) print(dataset,labels) #注意这里会改变输入数据的值,因为传入的是引用,del(labels[bestFeatureId]),这里应该传入list(x) tree=dtree.createTree(dataset,list(labels)) print(tree) #绘制决策树 tplt.createPlot(tree)
5.决策树的特点
如果匹配项太多,会引起“过度匹配”问题。这时候我们可以采用“裁剪”的方法,去掉一些不必要的叶子节点。如果叶子只能增加少许信息,则可以去掉该叶子节点或者跟其他叶子节点合并。这里使用的ID3算法无法处理数值型数据,尽管可以把数值型数据转化成标称类数据,但可能会产生太多划分,ID3算法会无法处理。ID3算法是一种贪心算法,用来构造决策树。ID3算法起源于概念学习系统(CLS),以信息熵的下降速度为选取测试属性的标准,即在每个节点选取还尚未被用来划分的具有最高信息增益的属性作为划分标准,然后继续这个过程,直到生成的决策树能完美分类训练样例。也可以采用CART算法构造决策树。




















 3211
3211

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








