codeforces 1402A (IOI, Unofficial Mirror Contest, Unrated) Fancy Fence

题目链接：

https://codeforces.com/problemset/problem/1402/A

题目大意：

给你n个矩形它们相互紧挨着，并且贴地，每个矩形都有一个整数宽度wi与整数高度hi，
现在问你在给定的矩形组合成的图形里有多少个子矩形（要求长宽为整数）

输入与输出：

input

2
1 2
1 2

output

样例解释：

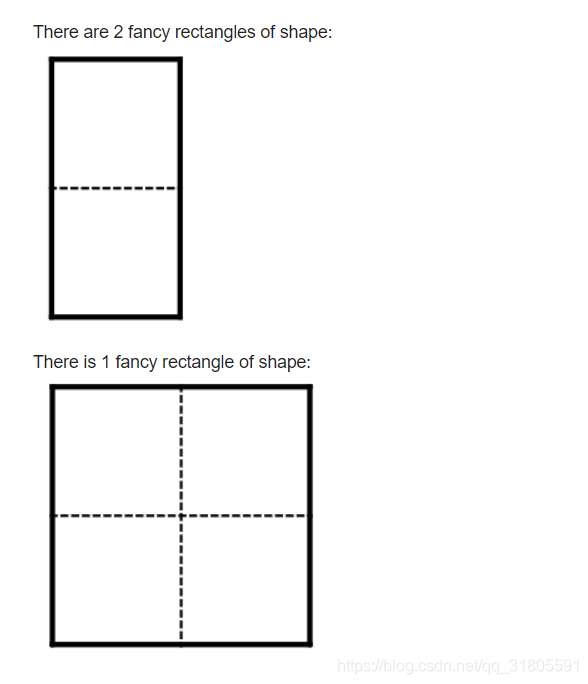
思路：

首先我们来解决对于一个大矩形看里面有多少个子矩形，
设一个大矩形长度为W宽度为H，那么其子矩形个数应该为：
(W * (W+1) / 2) * (H * (H+1) / 2)
(任意选择两个整数点为只矩形宽，任意选择两个整数点为只矩形高)

其次我们来解决不同的大矩形组合的问题，我们可以使用单调栈来解决，
在单调栈中，我们按照高度递增的保存矩形。
具体的：
设单调栈的最高矩形为H，新准备要push进一个高h的矩形
1.当h >= H, 则我们直接推入
2.当h < H, 则我们一直pop到单调栈的H >= h 或者单调栈为空，
之后使得当前准备推入的矩形的宽度为：
其本身宽度 + 刚才pop出的矩形的所有宽度和
而在pop时，我们计算结果。

具体如下图
我们就把当前单调栈所含的只矩形问题化成了求x个大矩形的只矩形的问题

但有两个注意点：
1：相邻两个大矩形会有重复计算的地方

1 2 间的

2：准备push进去的矩形和已存在矩形有重复的地方

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 5;
const int mod = 1e9 + 7;
#define int long long

struct node
{
	int ss;
	int hh;
	node(int ss, int hh) :
		ss(ss), hh(hh) {};
	node(){}
};
node sta[maxn];
node xx[maxn];
int res, n, Sid, Eid;

inline int getSize();
inline int modRes(int tempS);
int calRes(int width, int height);

signed main()
{
	while (scanf("%lld", &n) != EOF) {
		Eid = 0, res = 0;
		for (int i = 1; i <= n; i++) {
			scanf("%lld", &xx[i].hh);
		}
		for (int i = 1; i <= n; i++) {
			scanf("%lld", &xx[i].ss);
		}
		xx[n + 1].ss = 0;
		xx[n + 1].hh = 0;
		for (int i = 1; i <= n + 1; i++) {
			int tempS = 0;
			while (getSize() && xx[i].hh < sta[Eid].hh) {
				tempS += sta[Eid].ss;
				modRes(tempS);
				Eid--;
			}
			xx[i].ss += tempS;
			res -= calRes(tempS, xx[i].hh);
			res = (res + mod) % mod;
			sta[++Eid] = xx[i];
			//printf("i=%lld res=%lld\n", i, res);
		}
		printf("%lld\n", res);
	}
	return 0;
}

int getSize()
{
	return Eid;
}

int ppow(int x, int y)
{
	int res = 1;
	while (y) {
		if (y & 1) res *= x, res %= mod;
		y >>= 1;
		x *= x;
		x %= mod;
	}
	return res;
}

int calRes(int width, int height)
{
	width %= mod;
	height %= mod;
	return
		(height * (height + 1) % mod * ppow(2, mod - 2) % mod) *
		(width * (width + 1) % mod * ppow(2, mod - 2) % mod) % mod;
}

int modRes(int tempS)
{
	int hh = sta[Eid].hh;
	int ss = tempS % mod;
	int ps = (ss - sta[Eid].ss + mod) % mod;
	int tres = calRes(ss, hh) - calRes(ps, hh);
	res += (tres + mod) % mod;
	res %= mod;
	return 0;
}