概率
用来研究随机现象数据规律的数学分支
-
频率
A事件在N次试验中发生的次数与总试验次数的比值,fn(A) = nA/n
-
概率
fn(A)的稳定值P定义为该事件的概率
古典概型
试验E中样本点是有限的(个数确定),出现每一概率点的概率相同
条件概率
在某一个条件发生的前提下,另一个事件发生的概率。
- 样本空间:P(A/B)的样本空间为B,在B发生的前提下,A发生的概率。P(B)的样本空间为所有样本空间
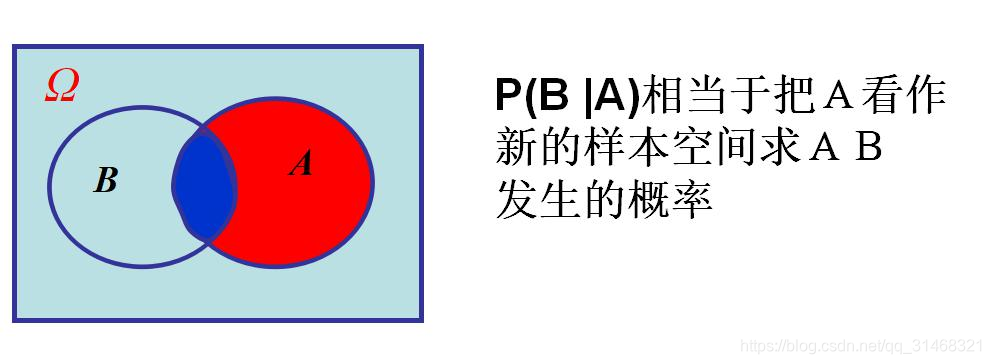
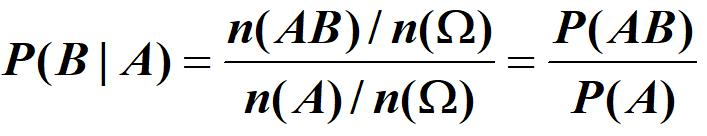
- 区分P(AB),P(B/A)
- 样本空间不同,前者为所有的样本空间,后者的样本空间为A
- 相同点是,A和B都发生了
独立性
若 P(B/A) = P(B) 即P(AB)=P(A)P(B),则A,B相互独立
独立试验
-
重复独立试验,在相同的条件下,将试验E重复进行,且每次试验是独立进行的,即每次试验各种结果出现的概率不受其他各次试验结果的影响
-
n重伯努利试验:若一试验的结果只有两个A和Ā, 在相同的条件下, 将试验独立地重复进行n次, 则称这n次试验所组成的试验为n重复伯努利试验或伯努利概型
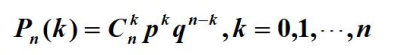
【q = 1-p】
二维随机变量
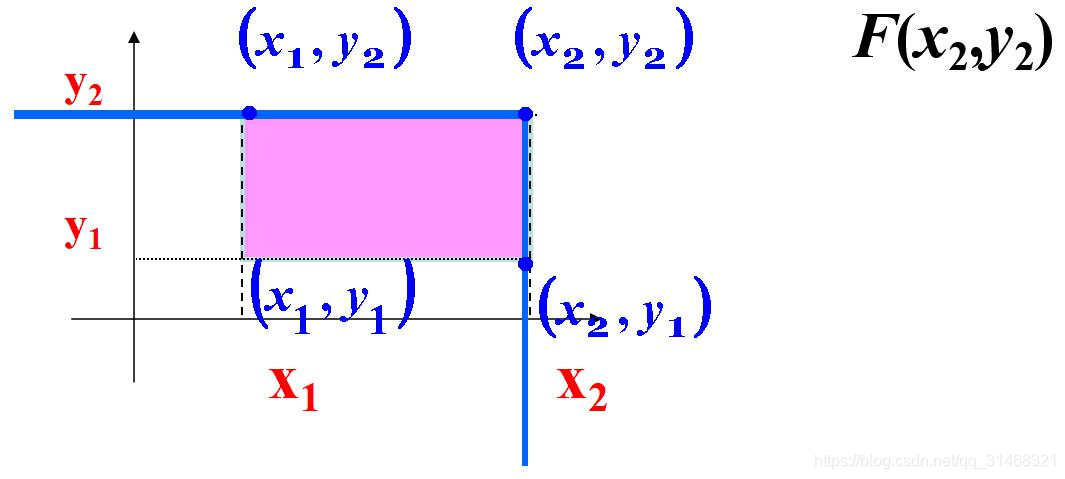
二维随机变量的联合函数:
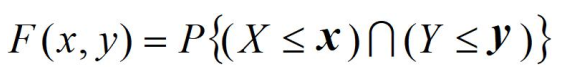
F(x,y)表示随机点(x,y)在以(x,y)为顶点且位于该点左下方无穷矩阵的内的概率
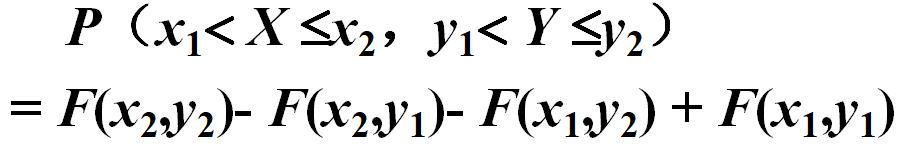
离散型随机变量的联合概率分布
若二维随机变量(X,Y)全部可能取到的不同值是有限对或可列无限对
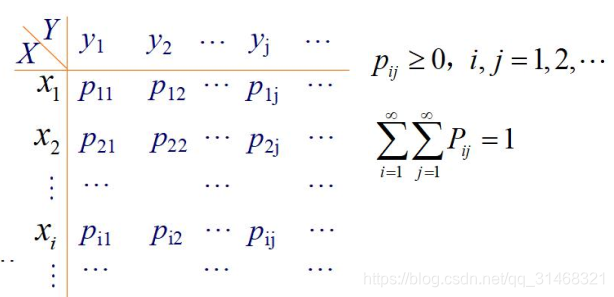
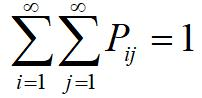
二维连续型随机变量
二维随机变量(X,Y)的分布函数F(X,Y)如果存在非负函数f(x,y),对于任意x,y有
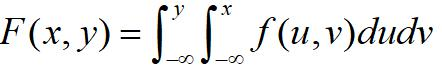
则称(x,y)为二维连续型随机变量。f(x,y)为概率密度
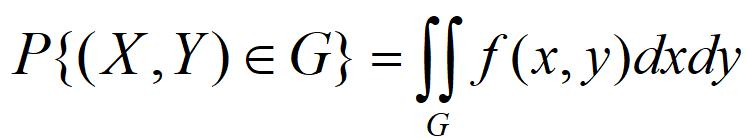
边缘分步
将分布函数F(x,y)的随机变量x趋近于正无穷,就可以得到FX(x).同理,可得到Fy(y).
Fx(x),Fy(y)称为边缘分步函数
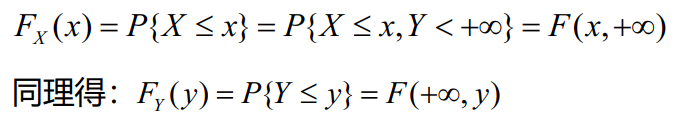
离散型的边缘分步
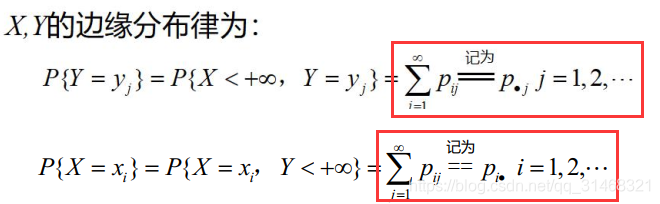
连续性的边缘概率密度
分别在指定定义域上对边缘概率密度函数求积分

期望
数学期望反应的是随机变量的取值水平
-
离散型随机变量的X的分布律:
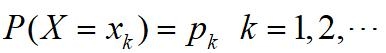
若,级数绝对收敛,则数学期望为:
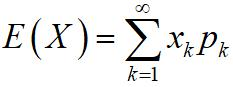
-
连续型随机变量的概率密度f(x),若xf(x)在定义域上积分绝对收敛,则数学期望为
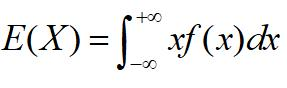
二维随机变量的期望
-
离散的
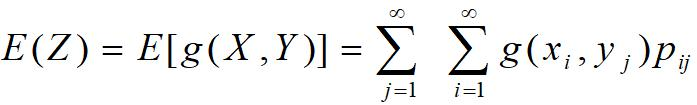
-
连续的

期望的性质

方差
方差反映了随机变量的相差与期望的分散程度
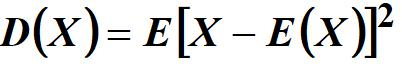
大数定理
在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率
中心极限定理
样本的平均值约等于总体的平均值不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且呈正态分布








 本文深入探讨了概率论在机器学习中的基础知识,包括古典概型、条件概率、独立性、大数定理和中心极限定理等核心概念。通过解析二维随机变量的联合概率分布、边缘概率密度以及期望和方差的计算,为机器学习的数学基础提供了清晰的理解。
本文深入探讨了概率论在机器学习中的基础知识,包括古典概型、条件概率、独立性、大数定理和中心极限定理等核心概念。通过解析二维随机变量的联合概率分布、边缘概率密度以及期望和方差的计算,为机器学习的数学基础提供了清晰的理解。
















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








