文章目录
1. RNN 基本原理
DNN 就是让输入
x
x
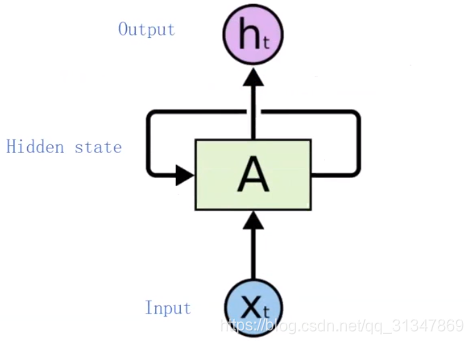
x 经历一个 network A,得到输出
y
y
y,是一个直线型的过程,而 RNN 提出了一个特有的结构,就是 A 上的环线,取名为 hidden state,它不仅作为输出,还作为下一个输入。
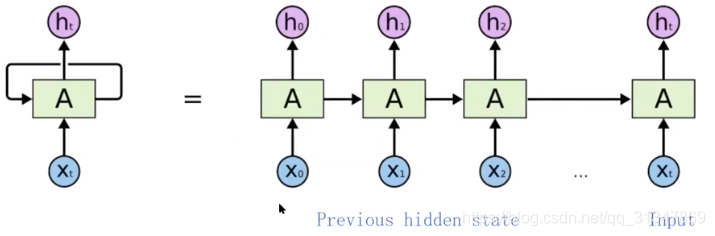
将 RNN 结构展开,更容易理解:RNN 的输入是一个序列 {
x
0
x_0
x0,
x
1
x_1
x1,
.
.
.
...
...,
x
t
x_t
xt}
DNN 与 RNN 输出公式的比较:
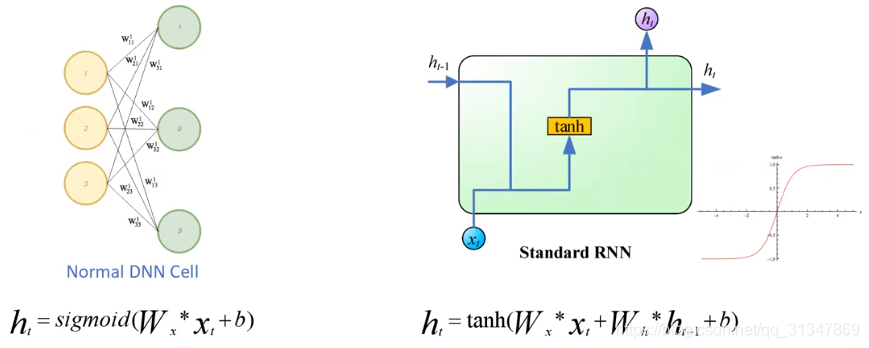
RNN 所做的工作是:在某一个 time step 预测一个 vector,预测的依据不仅来自于当前 time step 所获得的输入 x,还有 RNN 自身的前一个状态,所以我们就能为每一个 time step 的输出构建一个公式:
S
t
=
f
W
(
S
t
−
1
,
x
t
)
S_t=f_W(S_{t-1},x_t)
St=fW(St−1,xt)
- S t S_t St 是 t 时刻的状态,它可以是多个向量的集合, S t S_t St 可以说是一个新状态(new state)
- S t − 1 S_{t-1} St−1 是前一个时刻的状态,可以说它是一个旧状态(old state)
- x t x_t xt 是一个 time step 的输入向量
- f W f_W fW 包含了一些与参数 W W W 有关的 function,是训练过程中学习的
RNN 也可以像 DNN 一样扩展深度,只不过 RNN 的扩展有两个维度,一个是网络结构上的深度,另一个是输入序列上的长度:
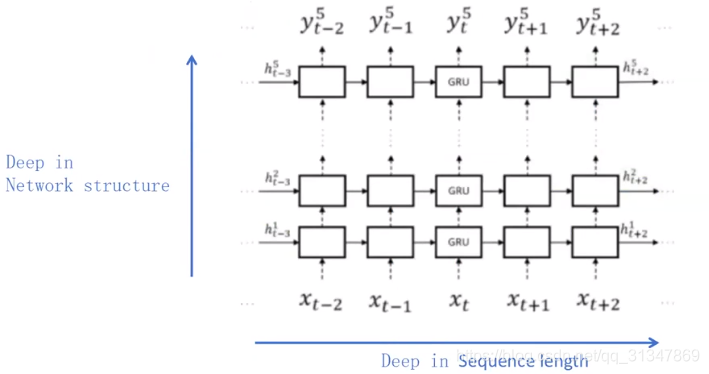
补充几点:
- 每一个 time step 内都使用同一个 f W f_W fW 和同一组参数设置
- f f f 一般是非线性的激活函数,比如 tanh 或 ReLU
- 在计算 S 0 S_0 S0时,理论上要用前一个状态,但其并不存在,所以通常将 S 0 S_0 S0 设置为 0 向量
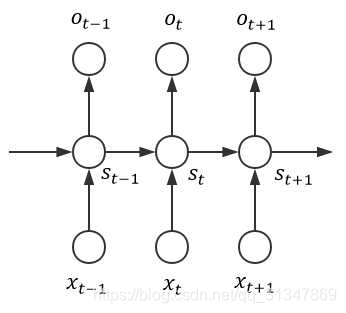
2. RNN 前向传导算法
令:x 表示输入,o 表示输出,S 表示隐藏层状态(S是网络的记忆单元)
我们已经知道 t 时刻的输出
o
o
o 是和 t 时刻的输入
x
x
x 以及 t-1 时刻的状态
S
S
S 有关的,所以
用
x
t
−
1
x_{t-1}
xt−1,
x
t
x_t
xt,
x
t
+
1
x_{t+1}
xt+1 分别表示第
t
−
1
t-1
t−1,
t
t
t,
t
+
1
t+1
t+1 时刻的输入;
用
o
t
−
1
o_{t-1}
ot−1,
o
t
o_t
ot,
o
t
+
1
o_{t+1}
ot+1 分别表示第
t
−
1
t-1
t−1,
t
t
t,
t
+
1
t+1
t+1 时刻的输出;
用
S
t
−
1
S_{t-1}
St−1,
S
t
S_t
St,
S
t
+
1
S_{t+1}
St+1 分别表示第
t
−
1
t-1
t−1,
t
t
t,
t
+
1
t+1
t+1 时刻隐藏层的状态;
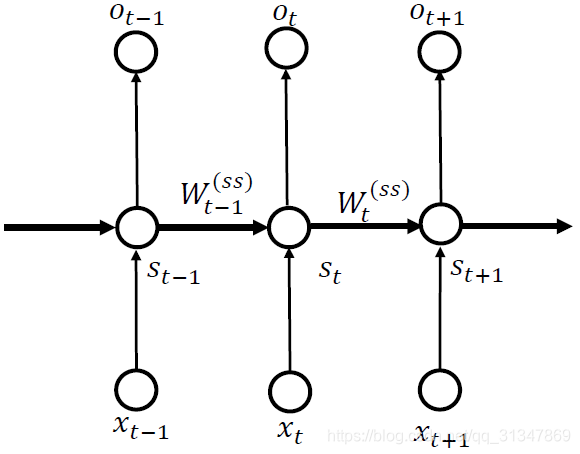
t
t
t 时刻的隐层状态:
S
t
=
W
t
(
x
s
)
x
t
+
W
t
−
1
(
s
s
)
S
t
−
1
S_t=W_t^{(xs)}x_t+W_{t-1}^{(ss)}S_{t-1}
St=Wt(xs)xt+Wt−1(ss)St−1
t
t
t 时刻的输出:
o
t
=
W
t
(
s
o
)
S
t
o_t=W_t^{(so)}S_t
ot=Wt(so)St
将
S
t
S_t
St 代入
o
t
o_t
ot 可得:
o
t
=
W
t
(
s
o
)
(
W
t
(
x
s
)
x
t
+
W
t
−
1
(
s
s
)
S
t
−
1
)
o_t=W_t^{(so)}(W_t^{(xs)}x_t+W_{t-1}^{(ss)}S_{t-1})
ot=Wt(so)(Wt(xs)xt+Wt−1(ss)St−1)
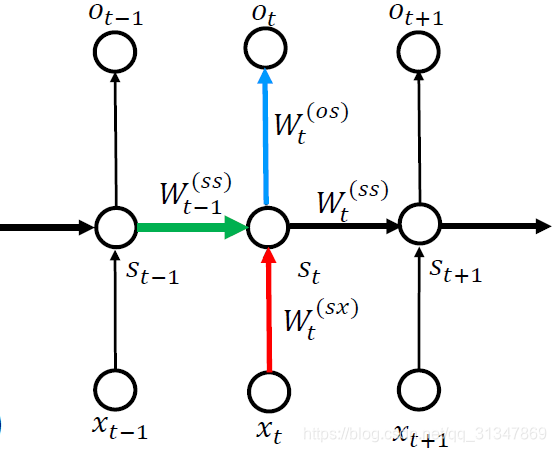
又由于 RNN 网络参数是共享的,即整个网络用作同一用途的参数
W
W
W 是相同的,于是令:
W
1
(
x
s
)
=
.
.
.
=
W
t
(
x
s
)
=
U
W_1^{(xs)}=...=W_t^{(xs)}=U
W1(xs)=...=Wt(xs)=U
W
1
(
s
s
)
=
.
.
.
=
W
t
(
s
s
)
=
W
W_1^{(ss)}=...=W_t^{(ss)}=W
W1(ss)=...=Wt(ss)=W
W
1
(
s
o
)
=
.
.
.
=
W
t
(
s
o
)
=
V
W_1^{(so)}=...=W_t^{(so)}=V
W1(so)=...=Wt(so)=V
改写 S t S_t St 和 o t o_t ot 可得:
s
t
=
U
x
t
+
W
S
t
−
1
s_t=Ux_t+WS_{t-1}
st=Uxt+WSt−1
o
t
=
V
S
t
=
V
(
U
x
t
+
W
S
t
−
1
)
o_t=VS_t=V(Ux_t+WS_{t-1})
ot=VSt=V(Uxt+WSt−1)
另外,一般认为初始状态
S
0
=
(
0
,
0
,
.
.
.
,
0
)
T
S_0 = (0,0,...,0)^T
S0=(0,0,...,0)T
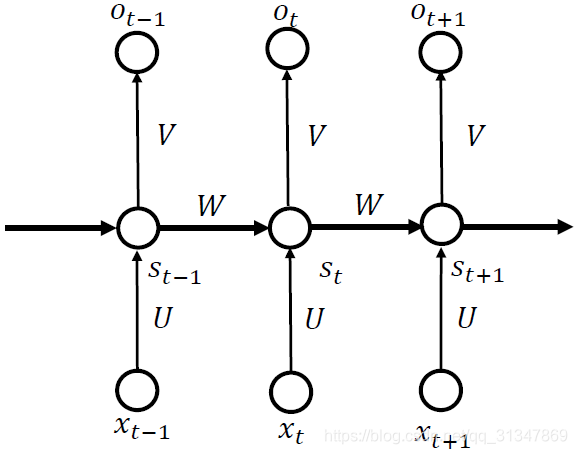
我们还知道神经网络中有激活函数的概念,那么 RNN 自然也可以有激活函数(这里将 S 视作隐藏层,o 视作输出层):
S
t
=
ϕ
t
(
x
s
)
(
U
x
t
+
W
S
t
−
1
)
S_t=\phi_t^{(xs)}(Ux_t+WS_{t-1})
St=ϕt(xs)(Uxt+WSt−1)
o
t
=
ϕ
t
(
s
o
)
(
V
S
t
)
=
ϕ
t
(
s
o
)
(
V
ϕ
t
(
x
s
)
(
U
x
t
+
W
S
t
−
1
)
)
o_t=\phi_t^{(so)}(VS_t)=\phi_t^{(so)}(V\phi_t^{(xs)}(Ux_t+WS_{t-1}))
ot=ϕt(so)(VSt)=ϕt(so)(Vϕt(xs)(Uxt+WSt−1))
而由于参数共享,两种激活函数 ϕ t ( x s ) \phi_t^{(xs)} ϕt(xs)、 ϕ t ( s o ) \phi_t^{(so)} ϕt(so) 通常分别取为相同的函数,即:
ϕ
1
(
x
s
)
=
.
.
.
=
ϕ
t
(
x
s
)
=
g
\phi_1^{(xs)}=...=\phi_t^{(xs)}=g
ϕ1(xs)=...=ϕt(xs)=g
ϕ
1
(
s
o
)
=
.
.
.
=
ϕ
t
(
s
o
)
=
f
\phi_1^{(so)}=...=\phi_t^{(so)}=f
ϕ1(so)=...=ϕt(so)=f
这样就得到最终的等式:
S
t
=
g
(
W
S
t
−
1
+
U
x
t
)
S_t=g(WS_{t-1}+Ux_t)
St=g(WSt−1+Uxt),
g
g
g 通常为 tanh 函数
o
t
=
f
(
V
S
t
)
=
f
(
V
g
(
W
S
t
−
1
+
U
x
t
)
)
o_t=f(VS_t)=f(Vg(WS_{t-1}+Ux_t))
ot=f(VSt)=f(Vg(WSt−1+Uxt)),
f
f
f 通常为 softmax 函数
隐藏层状态 S t S_t St 理论上应该包含前面所有 time step 的隐藏状态,但是在实际使用时,为了降低网络复杂度,通常 S t S_t St 只包含前面若干步(而非所有)的隐藏状态,同时输出 o t o_t ot 只与当前隐藏状态 S t S_t St 有关。
3. RNN 结构
3.1 经典 RNN 结构
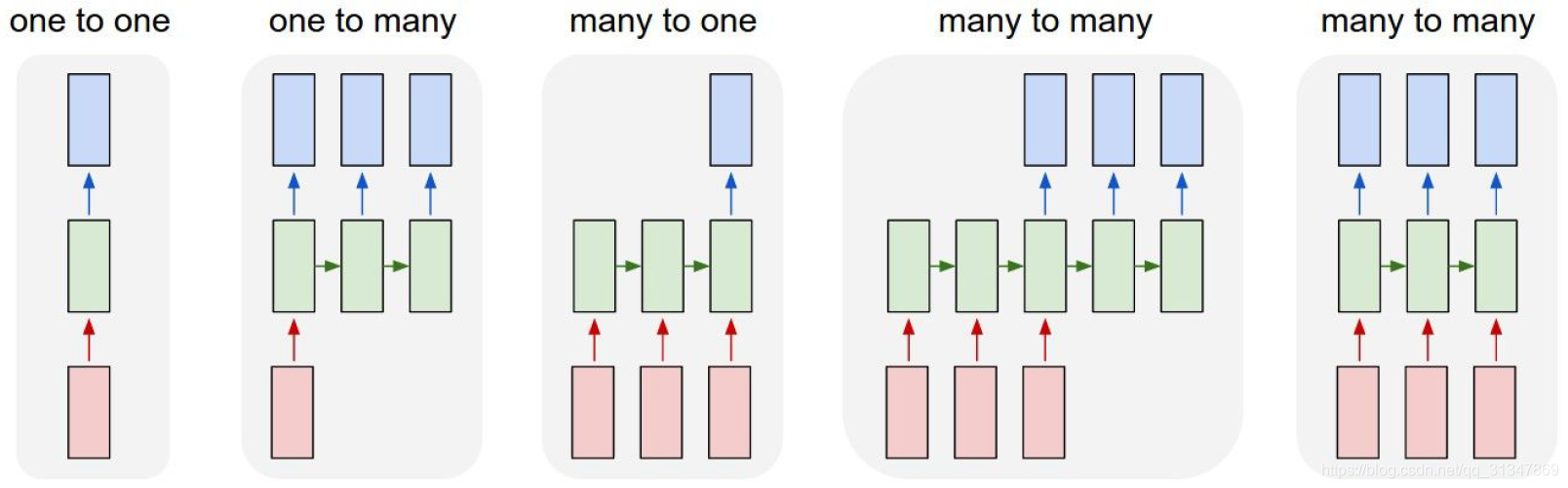
RNN 有很大的灵活性,下面是几种最典型的 RNN 结构:
- one to one(Vanilla Neural Network),是最朴素的 RNN 结构,可用于图像分类
- one to many(Image Captioning 看图说话)image -> sequence of words
- many to one(Sentiment Classification 情感分析)sequence of words -> sentiment
- many to many(Machine Translation 机器翻译)seq of words -> sq of words;(Video Classification on frame level 视频分类)
3.2 Bidirectional RNN
Bidirectional RNN 也可以叫做双向 RNN,它的输出
o
t
o_t
ot 取决于
S
t
S_t
St 和
h
t
h_t
ht,其中
S
t
S_t
St 是 t 时刻的状态,它取决于两个因素,上面已经讲过这里不再赘述;而
h
t
h_t
ht 就是双向 RNN 有别于基本 RNN 的地方,
h
t
h_t
ht 取决于 t 时刻的输入
x
x
x 和 t+1 时刻的状态
h
h
h(因为这里是从后向前传播),所以我们可以推得 t 时刻的输出
o
t
o_t
ot 为:
o
t
=
W
t
(
s
o
)
S
t
+
W
t
(
h
o
)
h
t
=
W
t
(
s
o
)
(
W
t
(
x
s
)
x
t
+
W
t
−
1
(
s
s
)
S
t
−
1
)
+
W
t
(
h
o
)
(
W
t
(
x
h
)
x
t
+
W
t
+
1
(
h
h
)
h
t
+
1
)
o_t=W_t^{(so)}S_t+W_t^{(ho)}h_t=W_t^{(so)}(W_{t}^{(xs)}x_t+W_{t-1}^{(ss)}S_{t-1})+W_t^{(ho)}(W_t^{(xh)}x_t+W_{t+1}^{(hh)}h_{t+1})
ot=Wt(so)St+Wt(ho)ht=Wt(so)(Wt(xs)xt+Wt−1(ss)St−1)+Wt(ho)(Wt(xh)xt+Wt+1(hh)ht+1)
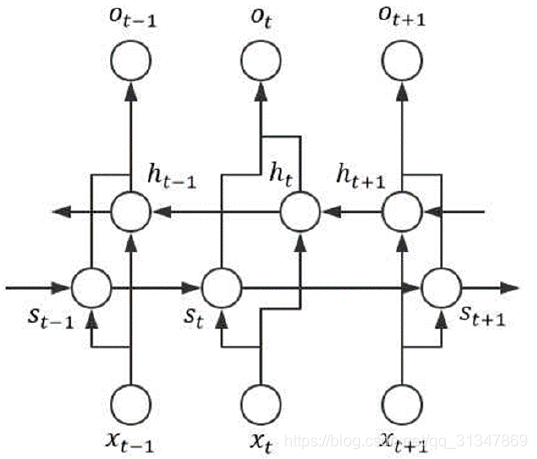
单向传递的 RNN 缺点在于,它可以利用历史信息,却无法利用未来信息。就好比在做阅读题时,我们往往需要“联系上下文”才能得出正确答案,如果能够让 RNN 利用未来信息,那么评估性能应该会更好。
3.3 深层 RNN
不论是基本的 RNN 结构还是双向 RNN 结构,都有一个共同的缺点,就是网络层数比较浅,因为每一个 time step 只有一个隐藏层 S,所以很自然就想要加深 RNN 网络的层数。
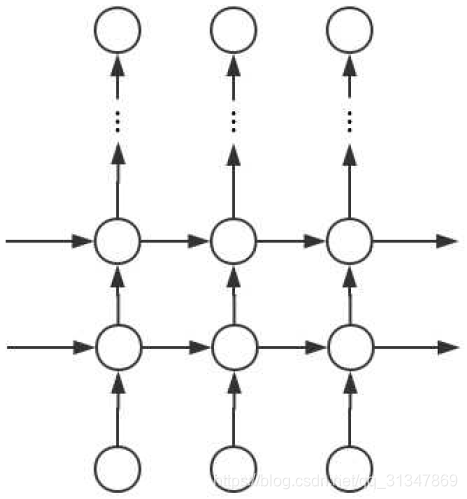
深层 RNN 每一步都有多层网络,所以该网络有更强的学习能力和表达能力,但同时复杂性也提高了,需要训练更多的数据。
4. BPTT 算法
BPTT(Back Propagation Through Time 时序反向传播)算法,主要难点在于各个 state 之间的通信,即梯度除了按照空间结构(
o
t
o_t
ot ->
S
t
S_t
St ->
x
t
x_t
xt)传播以外,还要沿着时间通道传播(
S
t
S_t
St ->
S
t
−
1
S_{t-1}
St−1 ->
.
.
.
...
... ->
S
1
S_1
S1),这样就难以写成一个统一形式,所以可以采用循环的方法来计算各个梯度。
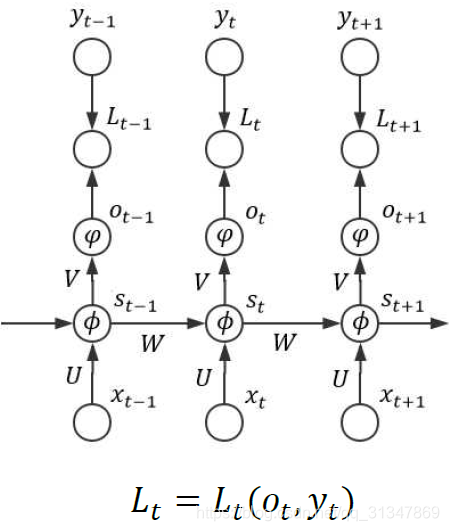
取
ϕ
\phi
ϕ 为隐藏层的激活函数
取
ψ
\psi
ψ 为输出层的变换函数
取
L
t
=
L
t
(
o
t
,
y
t
)
L_t=L_t(o_t,y_t)
Lt=Lt(ot,yt) 作为模型的损失函数,其中标签
y
t
y_t
yt 是 one-hot 向量
因为 RNN 处理的通常为序列数据(假设输入序列长度为 n),所以还可以计算接受完序列中所有样本后的总损失,此时模型的总损失可以表示为:
L
=
∑
t
=
1
n
L
t
L=\sum_{t=1}^{n}L_t
L=t=1∑nLt
由于输出 o t = ψ ( V S t ) = ψ ( V ϕ ( U x t + W S t − 1 ) ) o_t=\psi(VS_t)=\psi(V\phi(Ux_t+WS_{t-1})) ot=ψ(VSt)=ψ(Vϕ(Uxt+WSt−1)),其中 S 0 = ( 0 , 0 , . . . , 0 ) T S_0=(0,0,...,0)^T S0=(0,0,...,0)T
令
o
t
∗
=
V
S
t
o_t^*=VS_t
ot∗=VSt,
S
t
∗
=
U
x
t
+
W
S
t
−
1
S_t^*=Ux_t+WS_{t-1}
St∗=Uxt+WSt−1( * 表示 element wise 乘法)
则
o
t
=
ψ
(
o
t
∗
)
o_t=\psi(o_t^*)
ot=ψ(ot∗),
S
t
=
ϕ
(
s
t
∗
)
S_t=\phi(s_t^*)
St=ϕ(st∗)
从而有:(
×
\times
× 表示矩阵乘法)
∂
L
t
∂
o
t
∗
=
∂
L
t
∂
o
t
∗
∂
o
t
∂
o
t
∗
=
∂
L
t
∂
o
t
∗
ψ
′
(
o
t
∗
)
\frac{\partial L_t}{\partial o_t^*}=\frac{\partial L_t}{\partial o_t}*\frac{\partial o_t}{\partial o_t^*}=\frac{\partial L_t}{\partial o_t}*\psi'(o_t^*)
∂ot∗∂Lt=∂ot∂Lt∗∂ot∗∂ot=∂ot∂Lt∗ψ′(ot∗)
∂ L t ∂ V = ∂ L t ∂ V S t × ∂ V S t ∂ V = ( ∂ L t ∂ o t ∗ ψ ′ ( o t ∗ ) ) × S t T \frac{\partial L_t}{\partial V}=\frac{\partial L_t}{\partial VS_t}\times\frac{\partial VS_t}{\partial V}=(\frac{\partial L_t}{\partial o_t}*\psi'(o_t^*))\times S_t^T ∂V∂Lt=∂VSt∂Lt×∂V∂VSt=(∂ot∂Lt∗ψ′(ot∗))×StT
由
L
=
∑
t
=
1
n
L
t
L=\sum_{t=1}^{n}L_t
L=∑t=1nLt 得总梯度为:
∂
L
∂
V
=
∑
t
−
1
n
(
∂
L
t
∂
o
t
∗
ψ
′
(
o
t
∗
)
)
×
S
t
T
\frac{\partial L}{\partial V}=\sum_{t-1}^{n}(\frac{\partial L_t}{\partial o_t}*\psi'(o_t^*))\times S_t^T
∂V∂L=t−1∑n(∂ot∂Lt∗ψ′(ot∗))×StT
时间通道上的局部梯度:
∂
L
t
∂
S
t
∗
=
∂
S
t
∂
S
t
∗
∗
∂
L
t
∂
S
t
=
∂
S
t
∂
S
t
∗
∗
(
∂
S
t
T
V
T
∂
S
t
×
∂
L
t
∂
V
S
t
)
=
ϕ
′
(
S
t
∗
)
∗
[
V
T
×
(
∂
L
t
∂
o
t
∗
(
ψ
′
(
o
t
∗
)
)
]
\frac{\partial L_t}{\partial S_t^*}=\frac{\partial S_t}{\partial S_t^*}*\frac{\partial L_t}{\partial S_t}=\frac{\partial S_t}{\partial S_t^*}*(\frac{\partial S_t^TV^T}{\partial S_t} \times \frac{\partial L_t}{\partial VS_t})=\phi'(S_t^*)*[V^T \times (\frac{\partial L_t}{\partial o_t}*(\psi'(o_t^*))]
∂St∗∂Lt=∂St∗∂St∗∂St∂Lt=∂St∗∂St∗(∂St∂StTVT×∂VSt∂Lt)=ϕ′(St∗)∗[VT×(∂ot∂Lt∗(ψ′(ot∗))]
∂ L t ∂ S t − 1 ∗ = ∂ S t ∗ ∂ S t − 1 ∗ × ∂ L t ∂ S t ∗ = ∂ S t − 1 ∂ S t − 1 ∗ × ∂ S t ∗ ∂ S t − 1 × ∂ L t ∂ S t ∗ = ϕ ′ ( s t − 1 ∗ ) ∗ ( W T × ∂ L t ∂ S t ∗ ) \frac{\partial L_t}{\partial S_{t-1}^*}=\frac{\partial S_t^*}{\partial S_{t-1}^*} \times \frac{\partial L_t}{\partial S_t^*}=\frac{\partial S_{t-1}}{\partial S_{t-1}^*} \times \frac{\partial S_t^*}{\partial S_{t-1}} \times \frac{\partial L_t}{\partial S_t^*}=\phi'(s_{t-1}^*)*(W^T \times \frac{\partial L_t}{\partial S_t^*}) ∂St−1∗∂Lt=∂St−1∗∂St∗×∂St∗∂Lt=∂St−1∗∂St−1×∂St−1∂St∗×∂St∗∂Lt=ϕ′(st−1∗)∗(WT×∂St∗∂Lt)
再利用时间通道上的局部梯度计算 U 和 W 的梯度:
∂
L
t
∂
U
=
∑
k
=
1
t
∂
L
t
∂
S
t
∗
×
∂
S
t
∗
∂
U
=
∑
k
=
1
t
∂
L
t
∂
S
t
∗
×
x
t
\frac{\partial L_t}{\partial U} = \sum_{k=1}^{t}\frac{\partial L_t}{\partial S_t^*} \times \frac{\partial S_t^*}{\partial U} = \sum_{k=1}^{t}\frac{\partial L_t}{\partial S_t^*} \times x_t
∂U∂Lt=k=1∑t∂St∗∂Lt×∂U∂St∗=k=1∑t∂St∗∂Lt×xt
∂ L t ∂ W = ∑ k = 1 t ∂ L t ∂ S t ∗ × ∂ S t ∗ ∂ W = ∑ k = 1 t ∂ L t ∂ S t ∗ × S t − 1 \frac{\partial L_t}{\partial W}=\sum_{k=1}^{t}\frac{\partial L_t}{\partial S_t^*} \times \frac{\partial S_t^*}{\partial W}=\sum_{k=1}^{t}\frac{\partial L_t}{\partial S_t^*} \times S_{t-1} ∂W∂Lt=k=1∑t∂St∗∂Lt×∂W∂St∗=k=1∑t∂St∗∂Lt×St−1
5. LSTM 网络
全名为 Long-short term memory (LSTM) networks
5.1 RNN 的不足
RNN 可以看作是同一个神经网络的多次复制,每次使得信息从当前 step 传递到下一个 step,所以 RNN 的核心就是做当前的任务时,可以连接先前的信息。
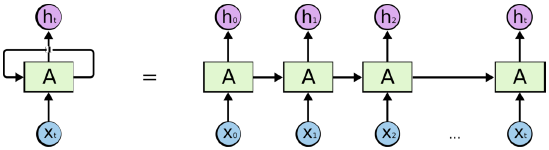
但关键是,只有当相关信息和预测词的位置之间的间隔非常小时,RNN 才可以学会使用先前的信息。
比如说:我学了八年法语,我能说一口很流利的_______。这时 RNN 就能很准确地预测出,接下来的词是“法语”。这就是相关信息和预测词之间的间隔比较小的情况(参考图5.1.2)。
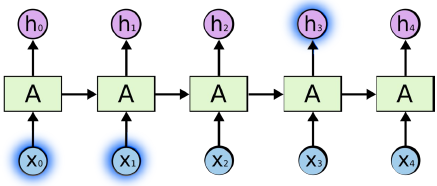
但是当场景变得复杂,相关信息和预测词之间的距离很远时,RNN 会丧失学习连接如此远的信息的能力。
比如说:我学了八年法语,因为我大学期间前往法国做交换生,而且到了那里之后我发现我非常喜欢这个国家,balabala,因此,我能说一口流利的_______。这就是相关信息和预测词之间的间隔比较大的情况(参考图5.1.3)。
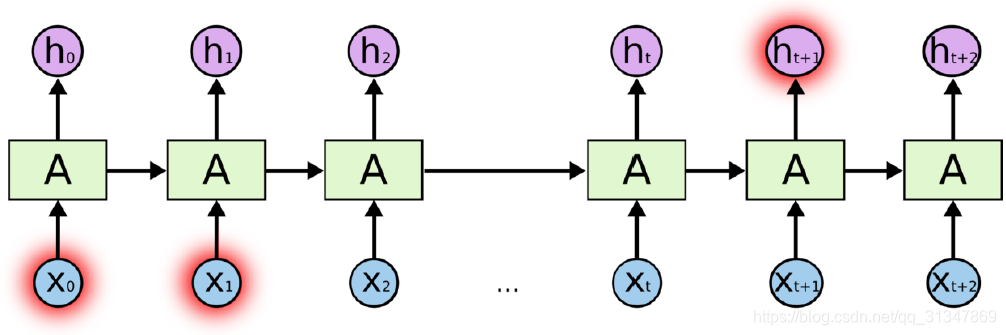
为什么 RNN 记不住更久远的信息?
因为传统 RNN 难以训练,罪魁祸首就是梯度消失和梯度爆炸 。因为训练时我们采用的是 Backward-propagation(gradient descent),当时间序列比较长时,梯度就可能消失到 0 或 发散到 NaN,我们很难给出一些合适的初始参数让网络进行稳定的训练。
在实际应用中,由于 RNN 会出现梯度消失和梯度爆炸问题,所以为了解决这些问题,就提出了经典了 LSTM。
5.2 LSTM简介
为什么 RNN 记不住很久远的信息,但 LSTM 就可以?
因为 LSTM 会选择性地忘记一些不重要的信息,把重要的信息关联在一起。RNN 的缺点正是 LSTM 所解决的,而且 LSTM 比 RNN 更容易训练。
LSTM(Long-Short Term Memort Networks)是一种特殊的 RNN 类型,优势在于可以学习长期依赖信息。
LSTM 相对于 RNN 的改变就是将 RNN 的每一个 state 看一个 cell,我们对这个 cell 的结构进行改进,从而实现一些复杂的功能。
对比 RNN 的 state 和 LSTM 的 cell:
在RNN中,cell 模块就只是一个很简单的结构,比如一个 tanh。
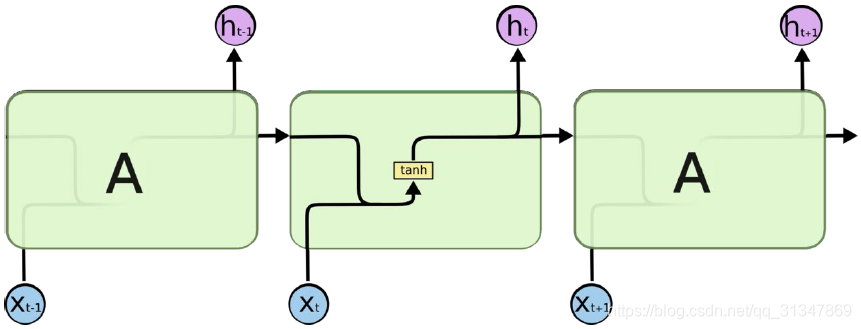
在 LSTM 中,cell 变得更加复杂,包含了 4 个结构进行交互。
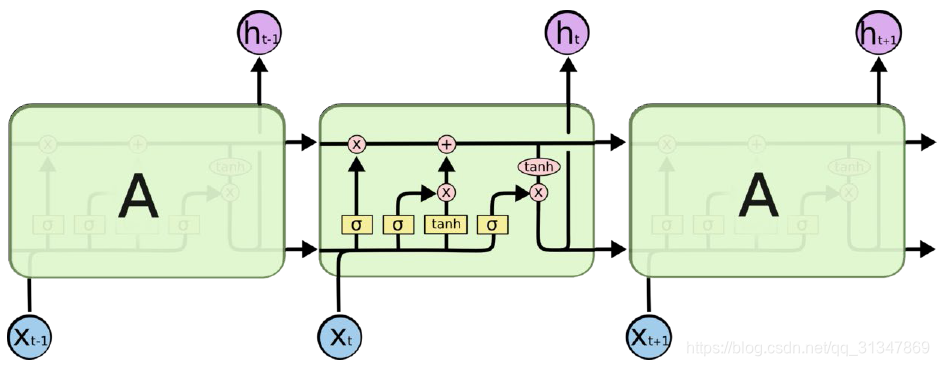
在每个 cell 中,每个黄色小方块就是一个 Neural Network Layer,每个粉色圆圈是一次运算操作。
5.3 LSTM结构
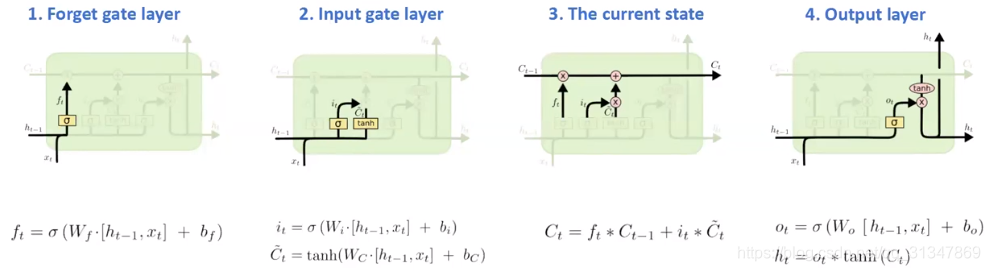
gate(门): LSTM 的特色就是 gate,通过这一结构达到去除或增加信息到细胞状态的能力,即 gate 就是一种让信息选择式通过的方法,它包含一个 sigmoid 层和一个 pointwise 乘法操作。
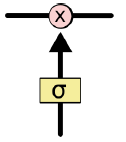
sigmoid 层输出 0 ~ 1 之间的数值,描述了每个部分有多少量可以通过。最极端的情况下,0 表示“不允许任何量通过(完全舍弃)”,1 表示“允许任意量通过(完全保留)”。
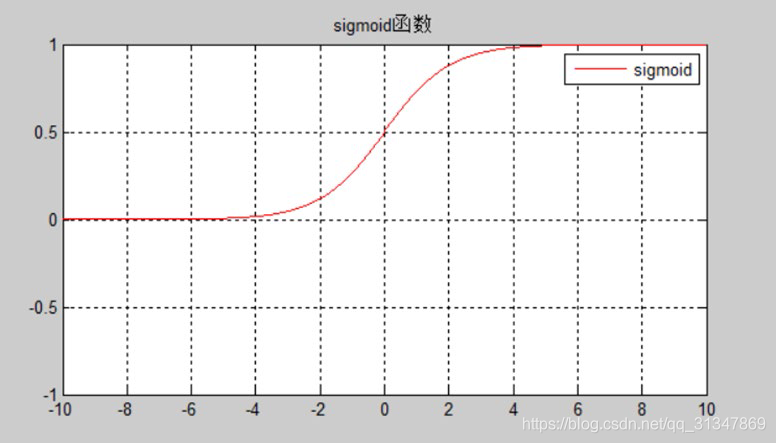
第一步: 第一个 sigmoid 层,称作 fotget gate(忘记门),它决定了从细胞状态中丢弃哪些信息。因为 LSTM 想要记住更长的信息,那么就要学会忘记一些不重要的信息。就好比我们在做视频分析时,相邻的几帧场景都差不多,那就没有必要记住所有的帧。
forget gate 会读取前一个输出
h
t
−
1
h_{t-1}
ht−1 和 当前输入
x
t
x_t
xt,判断当前这一帧有没有价值,输出一个 0 ~ 1 之间的数值
f
t
f_t
ft,让
f
t
f_t
ft 与细胞旧状态
C
t
−
1
C_{t-1}
Ct−1 进行点乘,丢弃掉需要丢弃的信息。
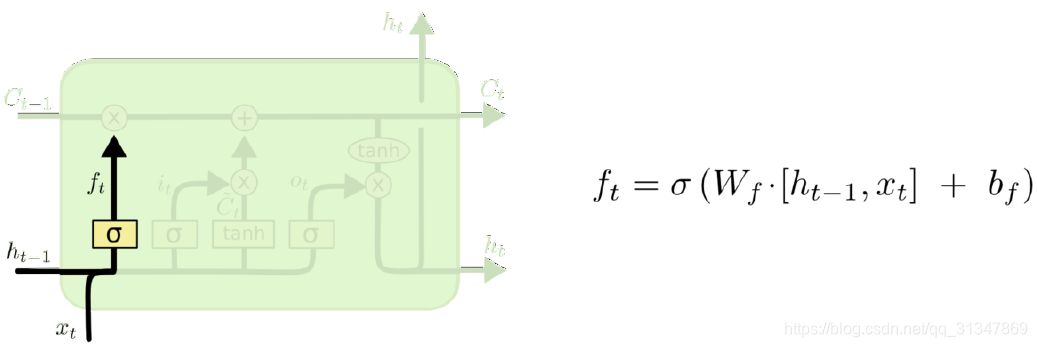
第二步: 包含了两部分,第二个 sigmiod 层和一个 tanh 层,它决定了什么样的新信息被存放在细胞状态中。
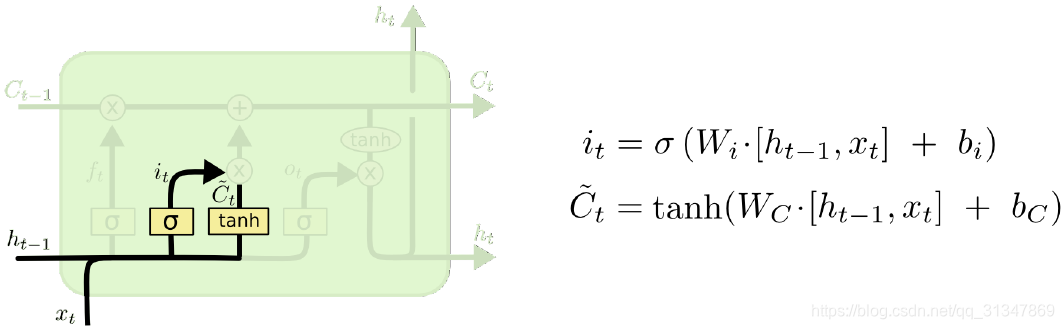
sigmoid 层称为“输入门层”,决定将要更新什么值;
tanh 层生成一个新的候选值向量
C
t
C_t
Ct,被加入到状态中
第三步: 将第一步得到的结果(选择丢弃之后)和第二步的结果进行相加。就得到了新的候选值
C
t
C_t
Ct
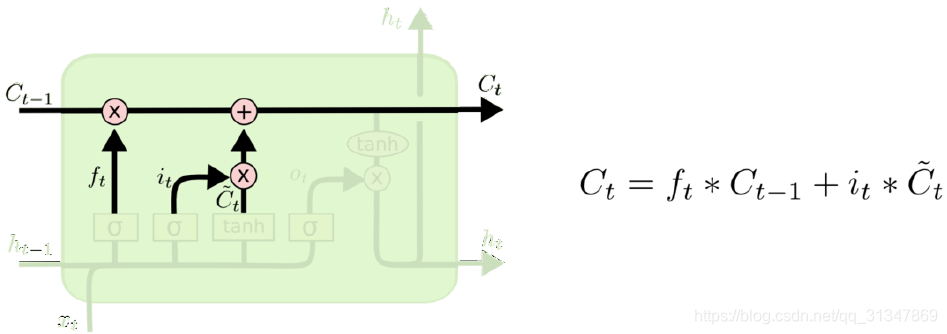
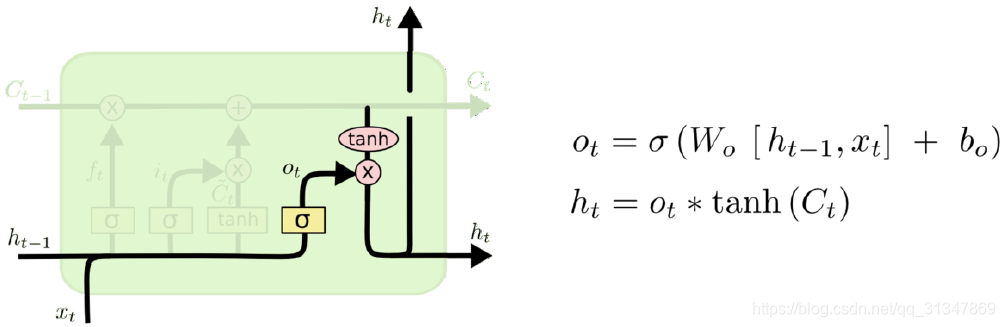
第四步:确定输出值。输出基于两个因素,一个是细胞状态,另一个是前一个输出。
- 使用 sigmoid 层来确定细胞状态的哪些部分将要输出
- tanh 对新的细胞状态进行处理(得到一个在 -1 到 1 之间的值)
- 将两者进行相乘,得到最后的输出
h
t
h_t
ht
5.4 LSTM的变体
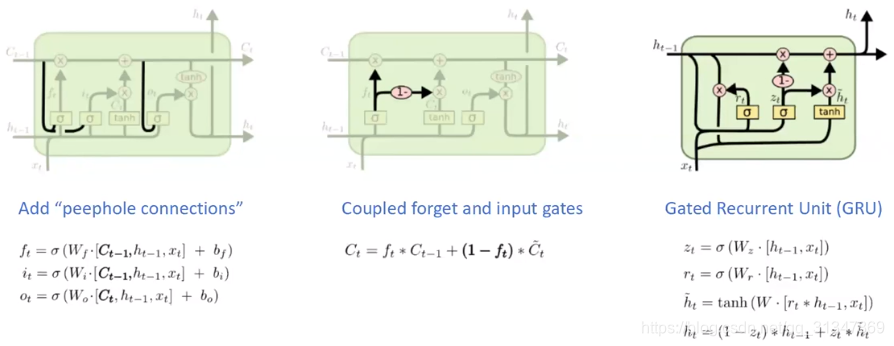
(1)在每个 gate 上增加 peephole,大部分论文中不是所有 gate 都会加
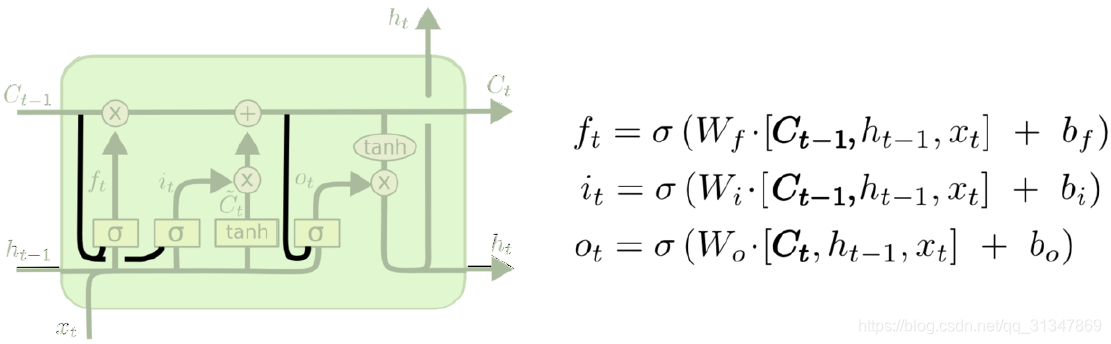
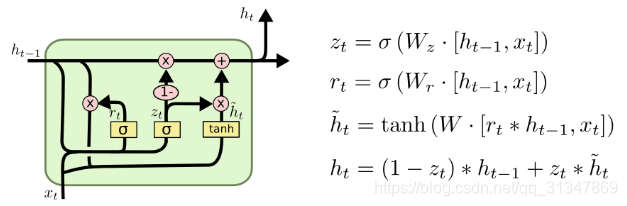
(2)另一个变体是通过使用 coupled 忘记和输入门。不同于之前是分开确定什么忘记和需要添加什么新的信息,这里是使用同一个门一同做出决定,这里
i
t
=
1
−
f
t
i_t=1-f_t
it=1−ft。
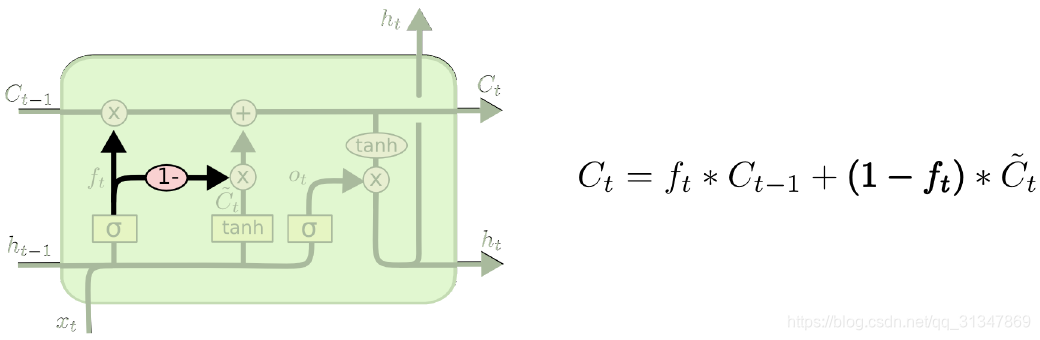
(3)





 本文深入探讨了RNN的基本原理、结构及算法,包括前向传导、BPTT算法,并详细解析了LSTM网络如何解决RNN长期依赖问题,通过门控机制实现信息的有效记忆与遗忘。
本文深入探讨了RNN的基本原理、结构及算法,包括前向传导、BPTT算法,并详细解析了LSTM网络如何解决RNN长期依赖问题,通过门控机制实现信息的有效记忆与遗忘。

















 4354
4354

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










