【读书笔记】数学之美2--自然语言处理

20.不要把鸡蛋放到一个篮子里--谈谈最大熵模型

在投资时常常讲不要把所有的鸡蛋放在一个篮子里，这样可以降低风险。因为如果你把大多数钱放在一个项目上，它一亏损则损失就十分之大，若平均着放入多个项目，则风险就会降到最小。在信息处理中，这个原理同样适用。在数学上，这个原理称为最大熵原理。

假设w3是要预测的词（王小波或者王晓波），w1和w2是它的前两个字（比如说它们分别是“出版”和“小说家”，），也就是其上下文的一个大致估计，s表示主题。则有：

          (20.1)

而这个模型的训练方法用的就是典型的：期望值最大化算法（EM）。

最原始的最大熵模型的训练方法是一种称为通用迭代算法GIS（Generalized Iterative Scaling）的迭代算法。GIS的原理并不复杂，大致可概括为以下几个步骤：

1. 假定第零次迭代的初始模型为等概率的均匀分布。
2. 用第N次迭代的模型来估算每种信息特征在训练数据中的分布。如果超过了实际的，就把相应的模型参数变小。否则，将他们变大。
3. 重复步骤2，直到收敛。

小结：从形式上看，它非常简单，非常优美；从效果上看，他是唯一一种既能满足各个信息源的限制条件，又能保证平滑性的模型。所以它的应用范围十分广泛。但是，最大熵模型计算量巨大，在工程上实现方法的好坏决定了模型的使用与否。

21.拼音输入法的数学原理

21.1 输入法与编码

输入法输入汉字的快慢取决于汉字编码的平均长度，通俗点讲，就是用击键次数乘以寻找这个键所需时间。对于汉字的编码分为两部分：对拼音的编码（参照汉语拼音即可）和消除歧义性的编码。像早期的双拼，虽然缩短了对拼音的编码，但其引入的歧义性十分之高；再后来的五笔输入法，它经常会导致人们思维的中断，所以速度不够快。最终，用户还是选择了拼音输入法，而且是每个汉字编码较长的全拼输入法。它解决了许多问题，最后只剩下排除一音多字的歧义性了。

21.2 输入一个汉字需要敲多少个键——谈谈香农第一定理

GB2312简体中文字符集一共有6700多个常用汉字。

假定每一个汉字出现的相对频率是：

     (21.1)

它们的编码长度是：

     (21.2)

那么，平均编码长度是：

     (21.3)

香农第一定理指出：对于一个信息，任何编码的长度都不小于它的信息熵。因此，上面平均编码长度的最小值就是汉字的信息熵，任何输入法都不可能突破信息熵给定的极限。

汉字的信息熵（根据第六章“信息的度量和作用”）：

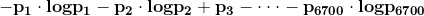     (21.4)

正如第六章所说的，自然语言处理的大量问题就是寻找相关的信息，以消除系统的不确定性。所以于此处，我们也应当寻找相关的信息，来减少每个汉字的平均信息熵。

最好的方法就是利用上下文，而利用上下文最好的方法是借助语言模型。利用语言模型将拼音串自动转成汉字，要有合适的算法。

21.3 拼音转汉字的算法

拼音转汉字的算法和在导航中寻找最短路径的算法相同，都是动态规划。

个人见解：其实这有点像机器翻译，同样需要利用上下文来推断出当前时刻的翻译应该是什么，但是又不全像。因为机器翻译是已知一整个句子，再进行翻译，能够知道“上下文”信息；但是拼音转汉字，是一个即时翻译的过程，只能够知道“上文”信息，所以可以说拼音转汉字的语言模型可以用“隐含马尔可夫模型”来模拟，它符合马尔可夫假设和独立输出假设。

语言模型的优化目标是（y是拼音串，w是汉字）：

     (21.5)

1. 可以取log，变成相加，易于求解；
2. 可利用beam-search搜索，使得求解值接近最值。

21.4 个性化的语言模型

因为上述的语言模型的语料库是建立在大众上的，所以可能不符合个人的需求。所以想到的办法是将个人的模型与大众的模型进行线性插值生成新的模型，成为自己电脑上的个性化的语言模型。

对于个人的语言模型的训练，最好的办法是找到大量符合用户经常输入的内容和用语习惯的语料，训练一个用户特定的语言模型。这里面的关键显然是如何找到这些符合条件的语料。如此又要用到余弦定理和文本分类的技术了。训练步骤如下：

1. 将训练语言模型的文本按照主题分成很多不同的类别，比如1000个，C1、C2，....，C1000。（可以用Keans分类等无监督学习分类算法？）
2. 对于每个类，找到它们的特征向量（TF-IDF）X1，X2，....，X1000。
3. 统计某个人输入的文本，得到他输入的词的特征向量Y。
4. 计算Y和X1，X2，....，X1000的余弦距离。
5. 选择前个K和Y距离最近的类对应的文本，作为这个特定用户语言模型的训练数据。
6. 训练一个用户特定的语言模型M1。

22.自然语言处理的教父马库斯和他的优秀弟子们

1. 马库斯用自己的影响力早早地开始建立了语料库，贡献了一大波力量；
2. 放手让博士生研究自己感兴趣的课题，这是他之所以桃李满天下的原因。马库斯高屋建瓴，能够很快地判断一个研究方向是否正确，省去了博士生很多做无谓尝试（Try-And-Error）的时间。

24.马尔科夫链的扩展--贝叶斯网络

24.1 贝叶斯网络

前面的章节中多次提到马尔科夫链，它描述了一种状态序列，其每个状态值取决于前面有限个状态。而在现实生活中，很多事物相互的关系并不能用一条链来串起来，很可能是交叉的、错综复杂的。

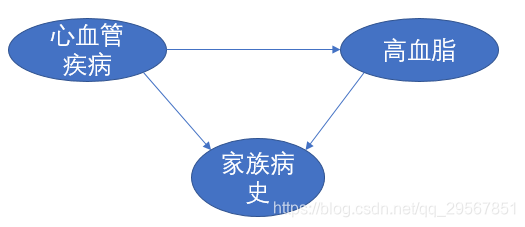
在网络中，每个节点的概率，都可以用贝叶斯公式来计算。而在计算贝叶斯网络中每个状态的取值时，只考虑了前面一个状态，这一点和马尔科夫链相同。可以讲，马尔科夫链是贝叶斯网络的特例，而贝叶斯网络是马尔科夫链的推广。

贝叶斯网络在图像处理、文字处理、支持决策等方面有很多应用。在文字处理方面，语义相近的词之间的关系可以用一个贝叶斯网络来描述。我们利用贝叶斯网络，可以找出近义词和相关的词，因而在Google搜索和Google广告中都有直接的应用。

个人见解：有点像深度学习当中词嵌入向量的学习，特别是Glove向量。语料库中两个词出现的频率就意味着贝叶斯网络中两者的置信度，而context和traget的词嵌入向量相乘描述的就是两者的相关性，通过cost函数使得两者的相关性向两个词于贝叶斯网络中的置信度靠近，便能够使得词嵌入向量的表征更加准确。

24.2 贝叶斯网络在词分类中的应用

前面的章节中提到的是“主题模型”：从一篇文章里得到它的特征向量，然后把整个特征向量通过余弦相似性对应到一个主题的特征向量。

Google工程师们利用贝叶斯网络，建立了文章、概念和关键词的联系，将上百万关键词聚合成若干概念的聚类，称为Phil Cluster。之后又有了Rephil，数据多了几百倍、考虑的关键词的相似性也从原来的再文本中同现扩展为上下文中同现，同时支持不同颗粒的概念。如此Rephil聚合了大约1200万个词，将它们聚合到上百万的概念中。一个概念一般有十几个到上百个词。

24.3 贝叶斯网络的训练

使用贝叶斯网络首先要确定它的结构。对于简单的问题可以直接给出，但是对于复杂的问题就无法人工给出结构了，需要通过机器学习得到。

优化的贝叶斯网络结构要保证它产生的序列（比如“家族病史”→“高血脂”→“心血管疾病”就是一个序列）从头到尾的可能性最大，如果是使用概率做度量，那就是后验概率最大。若用BFS或DFS，计算量巨大；若用贪心算法，则易陷入局部最优；若用蒙特卡洛方法，用许多随机数在贝叶斯网络中试一试，看看是否陷入局部最优，这个方法的计算量比较大。最新，新的放大是利用信息论，计算节点之间两两的无信息，只保留互信息较大的节点直接的连接，然后再对简化了的网络进行完备的搜索，找到全局优化的结构。

确定了结构后，就要确定节点之间的弧的权重了，假定这些权重用条件概率来度量。方法是利用一些训练数据，优化网络的参数，使得观察到的这些数据的后验概率达到最大。这个过程就是EM过程。

最后，需要知名结构的训练和参数的训练通常是交替进行的。也就是先优化参数，再优化结构，然后再次优化参数，直至得到收敛或者误差足够小的模型。

从数学层面讲，贝叶斯网络就是一个加权的有向图，是马尔科夫链的扩展。从认识论层面讲，它可以把任何有关联的事件统一到它的框架下面。

25.条件随机场、文法分析及其他

条件随机场是计算联合概率分布的有效模型。

之前提到的隐含马尔可夫模型，输出只和当前状态有关：

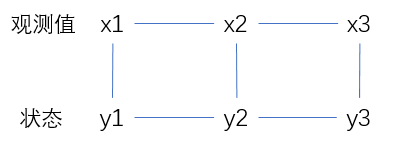
而对于条件随机场，其输出不仅与当前状态，与前后状态都有关：

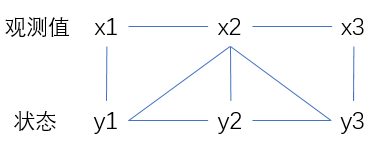
广义地讲，条件随机场是一种特殊的概率图模型。它的特殊性在于，变量之间要遵守马尔可夫假设，即每个状态的转移概率只取决于相邻的状态，这一点，它和我们前面介绍的另一种概率图模型——贝尔斯网络相同。而它们的不同之处在于，条件随机场是无向图，而贝叶斯网络是有向图。

在大部分应用中，条件随机场的节点分为状态节点的集合Y和观察变量节点的集合X。整个条件随机场的量化模型就是这两个集合的联合概率分布模型P(X,Y)