二叉树是一棵树,其中每个节点不多于两个儿子。二叉树是有顺序的,左孩子的值小于根节点的值小于右孩子的值,次序 不能改变。正因为这个特点才可以方便快捷的查找。
class BinaryNode{
Object element; //节点值
BinaryNode left; //左孩子
BinaryNode right; //右孩子
}对于二叉树的定义如上。
二叉树遍历通常有三种包含有先序、中序、后序三种顺序。还有层次遍历,类似与广度优先。
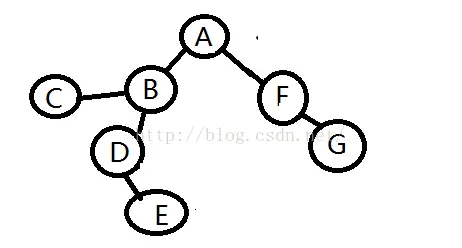
此图的ABCD仅仅表示这个点,不表示大小先后。
先序遍历顺序是:根节点->左孩子->右孩子
中序遍历顺序是:左孩子->根节点->右孩子
后序遍历顺序是:左孩子->右孩子->根节点
还原二叉树只需 先序|后序+中序,便可以完成重构。对于真二叉树(所有节点度数是偶数,即0或2),先序+后序也可以,但是如果不是真二叉树不行,因为有可能左孩子右孩子是空,会出现歧义。
先序遍历递归方法:
private void PreTraverse(BinaryNode x,Visit visit){
if(!x = null) //递归一定要有基准情况
return;
Visit(x); //根节点
PreTraverse(x.left,visit); //递归访问左孩子
PreTraverse(x.right,visit);//递归访问右孩子
}一般来说递归的量少还好,数据量大的话递归是很难实现的。遍历的迭代方法依靠栈实现。
先序遍历迭代方法:
private void goLeft(BinaryNode x,Visit visit,Stack<BinaryNode> s){
while(x){
Visit(x);
S.push(x.right); //右孩子入栈
x = x.left; //沿左链向下
}
}
private void PreIterTraverse(BinaryNode x,Visit visit){
goLeft(x,visit,s); //访问左子树,右子树入栈
if(s.empty()) break;//直到所有节点处理完
x = s.pop(); //访问右子树
}这种方法采用的思想很独特,先是从根节点出发,沿左链一次向下遍历左孩子,同时将右孩子入栈,当左孩子都访问完了,弹出栈顶元素即右孩子继续访问,和上述情况一样直到栈空为止。
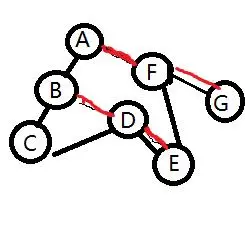
就像这张图一样,黑色代表访问顺序,红色代表入栈。(图画的较丑,凑合看看)先访问ABC,将FD依次入栈,C之后没有左孩子,即执行弹出栈操作,先弹出D,E入栈,在弹出栈顶的E,因为没有孩子,所以访问E之后继续弹出F,右孩子G入栈,出栈,访问结束。
第二种先序迭代方法:
private void PreIterTraverse2(BinaryNode x,Visit visit){
Stacks<BinaryNode> s;
if(x) s.push(x);
while(!s.empty()){ // 栈变空之前反复
x = s.pop();//根节点入栈
Visit(x);
if(HasRChild(x)) s.push(x.right);//右孩子入栈
if(HasLChild(x)) s.push(x.left); //左孩子入栈
}
}注意左右孩子的入栈顺序,因为采用的是栈,先进后出,所以右孩子先入栈。
中序遍历的递归方法就是先序遍历换一下访问顺序,就不赘述了。
中序遍历的迭代方法:
private void goLeft(BinaryNode x,Stacks){
while(x)
s.push(x); //沿左分支深入依次入栈
x = x.left;
}
private void InIterTraverse(BinaryNode x,Visit visit){
Stack<BinaryNode> s;
goLeft(x,s);
if(s.empty()) break;//直到所有节点处理完
x = s.pop();
vitit(x);
x = x.right;
}有了上面的先序遍历思路,这个应该不难理解,先是goLeft沿左子树不断向下,左子树依次入栈,栈为空终止,不为空弹出栈顶元素,访问并将他的右子树在goleft.
以上图为例,先是ABC入栈,C没有左子树所以执行弹出栈顶元素,即为C弹出,访问C之后,没有右子树,所以弹出B,访问B且X=D,把D入栈,在弹出D,访问D,D的右子树E赋给X,X=E,E入栈,出栈,访问,当E结束之后没有子树了,就继续弹栈,现在栈只有A,即弹出A,访问A,将F入栈,后F没有左子树,将F弹出,访问F,并X=G,G没有子树,所以最后弹出访问,栈为空,结束遍历。以每一个节点为根的树都是按照左中右结构遍历的。
后序遍历同理不赘述了。
最后来说一下层次遍历,类似于广度优先,把这一层的同一深度的遍历完再遍历下一层的,依靠队列实现。
private void LevelTraverse(Visit visit){
Queueq <BinaryNode> q;
q.enqueue(this); // 根节点入队
while(!q.empty){
BinaryNode x = q.dequeue(); //取出节点
visit(x);
if(HasLChild) s.enqueue(x.left); //左孩子入队
if(HasRChild(x)) s.enqueue(x.right); //右孩子入队
}
}




 本文详细介绍了二叉树的基本概念及其三种主要遍历方式:先序、中序和后序遍历。不仅提供了递归实现方法,还讨论了利用栈进行迭代遍历的技术细节。此外,文章还涉及了层次遍历的概念及其实现。
本文详细介绍了二叉树的基本概念及其三种主要遍历方式:先序、中序和后序遍历。不仅提供了递归实现方法,还讨论了利用栈进行迭代遍历的技术细节。此外,文章还涉及了层次遍历的概念及其实现。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








