聚类算法实现流程

聚类算法实现流程

1 k-means聚类步骤

1. 初始化：首先，随机选择K个数据点作为初始的聚类中心。
2. 分配簇：对于数据集中的每个样本点，计算其与当前所有聚类中心的距离，然后将该样本点分配到距离最近的聚类中心所在的簇。
3. 重新计算中心点：在每个簇中，重新计算新的中心点。通常，新的中心点是该簇中所有样本点的均值。具体来说，对于每个簇，将该簇内所有样本点的特征值分别求平均，得到新的中心点坐标。
4. 更新和迭代：如果新计算的中心点与之前的中心点不同，则使用新的中心点重复步骤2和3。这个过程会一直持续，直到中心点不再发生变化，或者达到预设的迭代次数

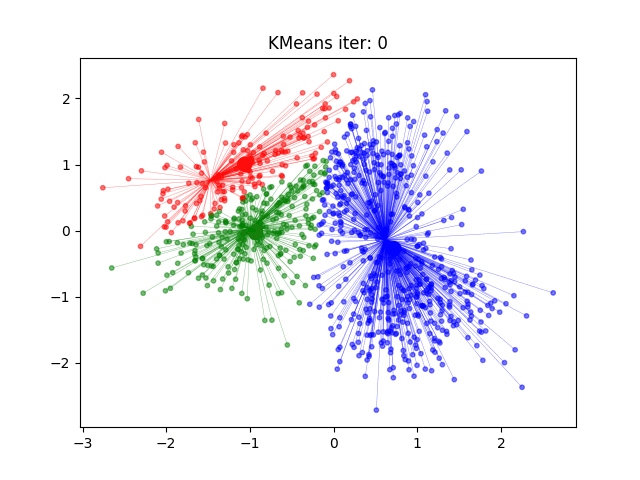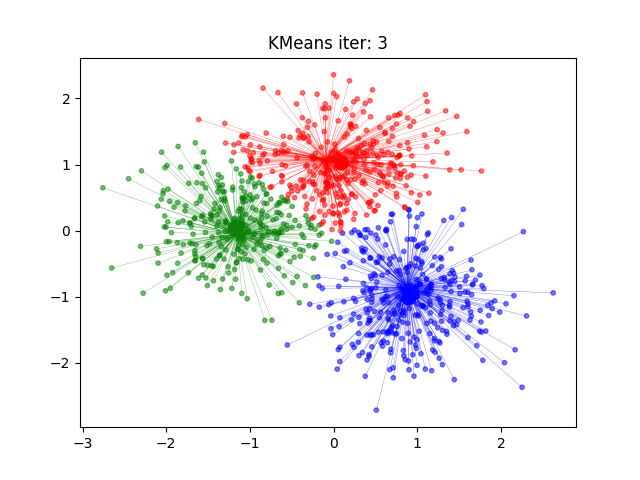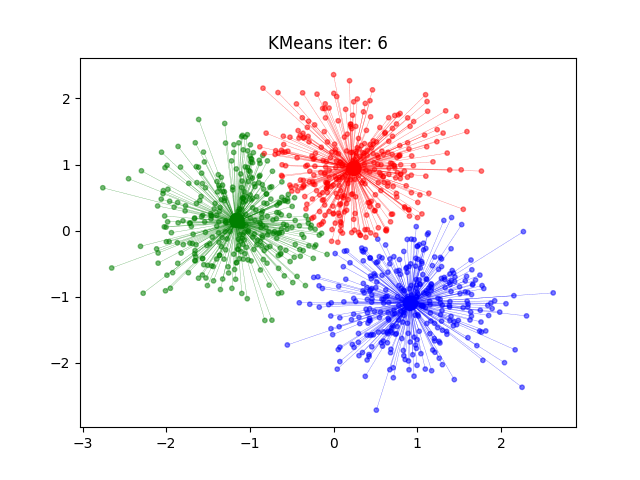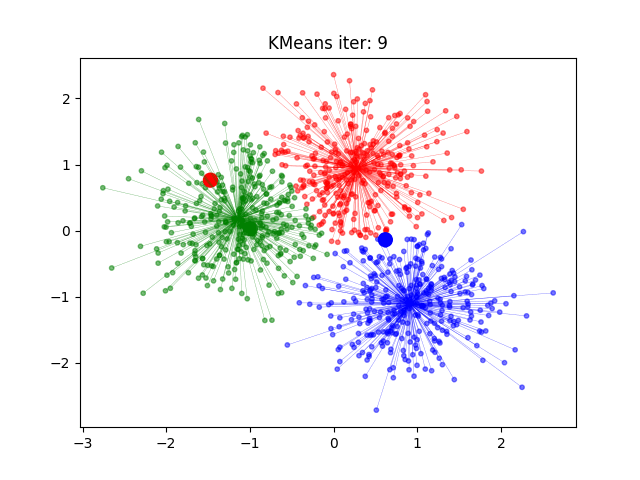
通过下图解释实现流程：

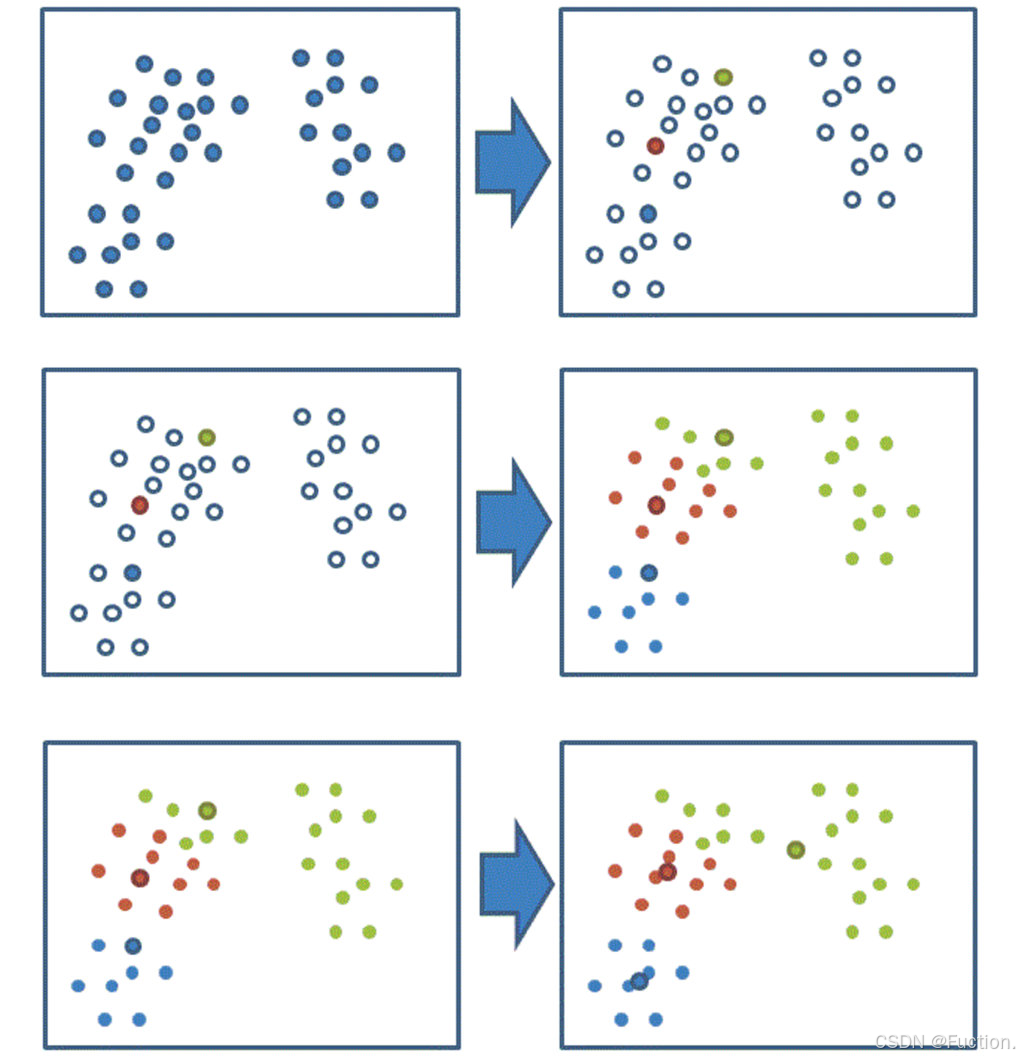
k聚类动态效果图

2 案例练习

• 案例：

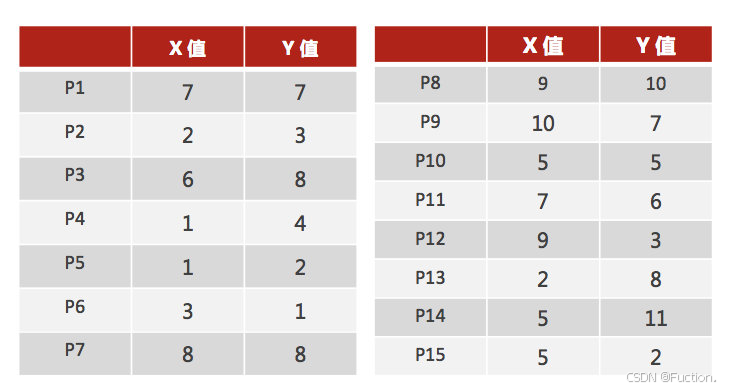
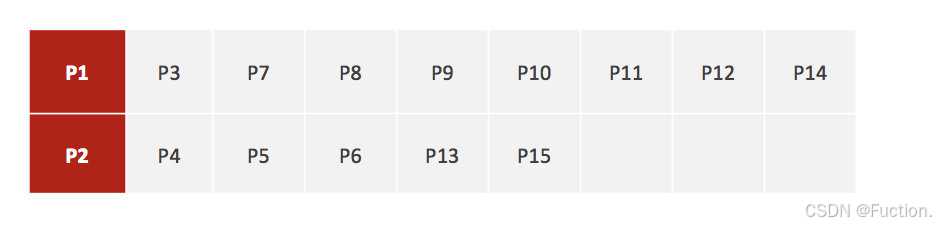
• 1、随机设置K个特征空间内的点作为初始的聚类中心（本案例中设置p1和p2）

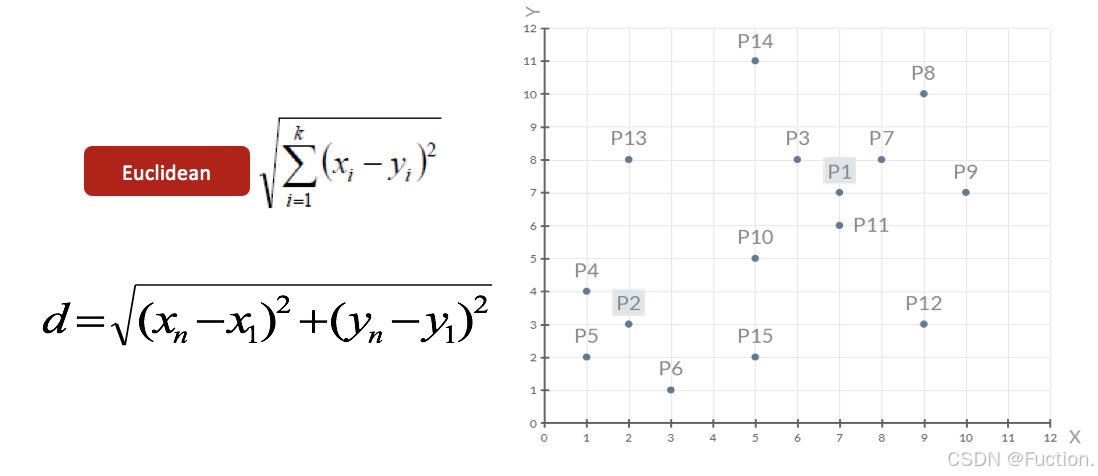
2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别

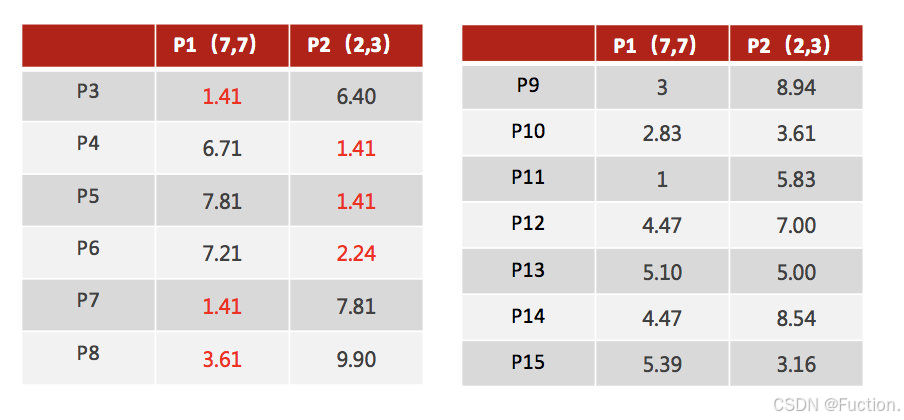
3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）

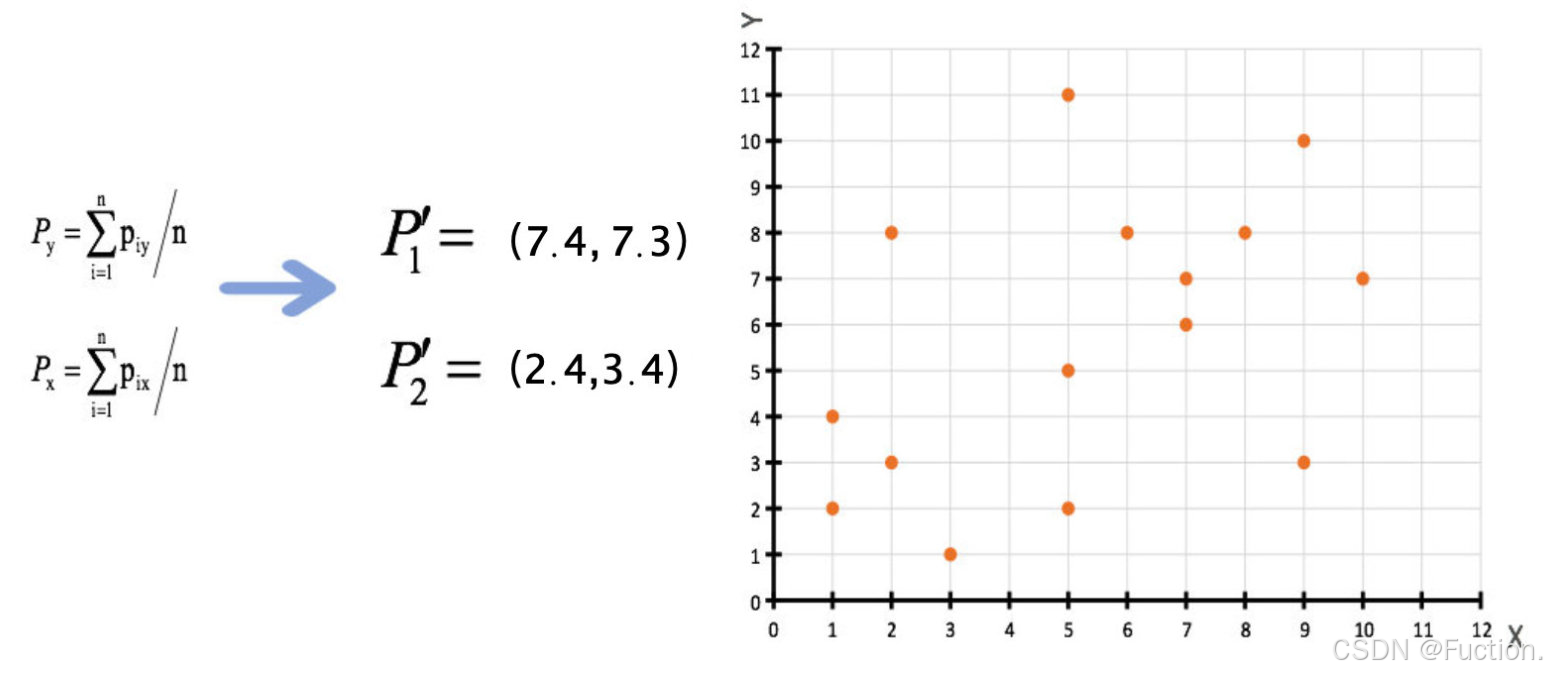
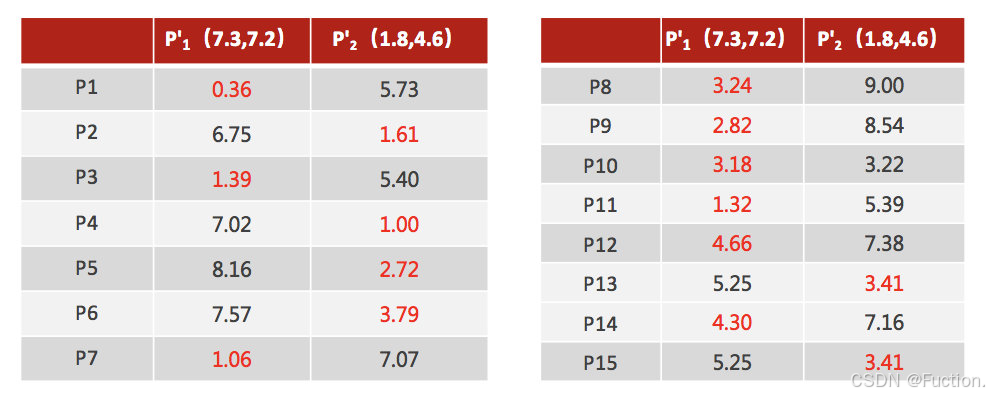
4、如果计算得出的新中心点与原中心点一样（质心不再移动），那么结束，否则重新进行第二步过程【经过判断，需要重复上述步骤，开始新一轮迭代】

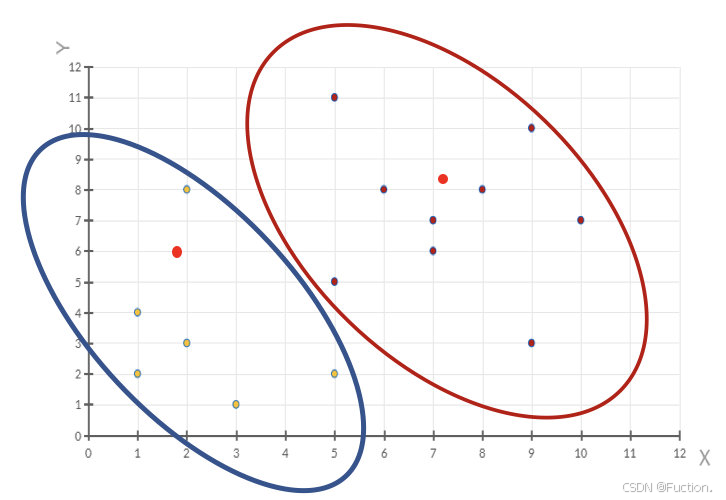
5、当每次迭代结果不变时，认为算法收敛，聚类完成，K-Means一定会停下，不可能陷入一直选质心的过程。

---

3 小结

• K-means聚类实现流程 
  • 事先确定常数K，常数K意味着最终的聚类类别数;
  • 随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，
  • 接着，重新计算每个类的质心(即为类中心)，重复这样的过程，直到质心不再改变，
  • 最终就确定了每个样本所属的类别以及每个类的质心。
  • 注意:
    • 由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。