算法学习——回溯法

回溯法

基本思路

回溯法是一种在解空间搜索问题的解的方法。它在问题的解空间树中，按深度优先策略，从根节点出发搜索解空间树。算法搜索至解空间的任一节点时，先判断该节点是否包含问题的解。若不包含，则跳过对该节点为根的子树的搜索，逐层向其祖先节点回溯；否则进入该子树，继续按深度优先策略搜索。用回溯法求解问题的所有解时，要回溯到问题的根，且根节的所有子树都被搜索遍才结束。用回溯法求问题的一个解时，只要搜索到问题的一个解就可以结束。这种以深度优先方式系统搜索问题解的算法称为回溯法。
问题的解一般表示成解向量或$n$元组$(x_1,x_2,...,x_n)$。给定问题，所谓问题的解空间就是解向量$(x_1,x_2,...,x_n)$的定义域。

算法框架

求解一个解向量

space为解空间，它的结构为space[i]为$x_i$的取值范围，Violatec为判断是否违背问题所附带的条件，True为违背，False为不违背。
sindex为解向量

i=0
j=0
while i<n:	                    #枚举每个分量
    while j<len(space[i]) and Violatec(space,sindex,i,j):
        j+=1
    if j<len(space[i]):	        #设置新分量，继续
        sindex[i]=j
        i+=1
        j=0
    else:	                    #回溯到上次发现的分量，并试探不同的一个
        i-=1
        if i<0:
            return
        j=sindex[i]+1
if i>=n:
    Output(space,sindex)
else:
    Output('no solution found')

求解全部解向量

i=0
j=0
while i>=0:	                    #枚举每个分量
    while j<len(space[i]) and Violatec(space,sindex,i,j):
        j+=1
    if j<len(space[i]):	        #设置新分量，继续
        sindex[i]=j
        i+=1
        j=0
    else:	                    #回溯到上次发现的分量，并试探不同的一个
        i-=1
        if i<0:
            break
        j=sindex[i]+1
    if i>=n:                    #当得到一个解向量后，输出，并继续寻找其余解
        Output(space,sindex)
        i=n-1
        j=sinde[n-1]+1
Output('no more solution')

八皇后问题

假设在$8\ast 8$的棋盘上要放8个皇后，使得没有任何两个皇后在同一行、同一列，或同一条对角线上。

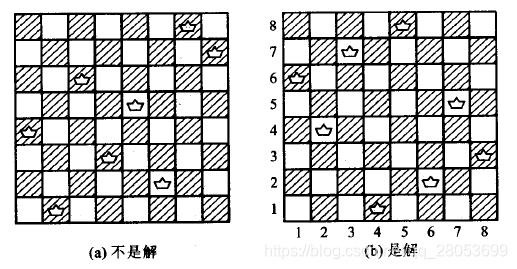
该棋盘的行号和列号都是$1,2,...,n$，皇后也用$1,2,...,n$来命名。令皇后$i$在第$i$列上，这样就满足了各皇后必须在不同列上的要求。于是所有皇后可以表示成$(x_1,x_2,...,x_n),n=8$。其中$x_i$是皇后i所在行号。本例的显约束条件为
x∈Si={1,2,...,8},1≤i≤8x \in S_i=\{ 1,2,...,8\},1\leq i\leq 8x∈Si​={1,2,...,8},1≤i≤8
解空间由$8^8个8元组构成$。隐约束条件为：
1.对任意的$i≠j$，应有$x_i≠x_j$；
2.任意两皇后应不在同一对角线上。

第一个约束条件表明任何一个解都是1,2,…8的一个排列，这使解空间大小从$8^8$减小到$8!$。
借助棋盘的标号，约束条件2的判别很简单，在上述棋盘中，当一个皇后从左下方走向右上方时，“行标号-列标号”的值不变，当一个皇后从左上方走向右下方时，“行标号+列标号”的值不变。设$x_j$与$x_l$的位置为$(i,j),(k,l)$，若这两个皇后在同一对角线上，则有$$i+j=k+l或i-j=k-l$$变换一下形式便可得$$j-l=k-i或j-l=i-k$$即$$|j-l|=|i-k|$$
因此当且仅当$|j-l|=|i-k|$时，两个皇后在同一对角线上。
接下来先求解八皇后问题的一个解，然后再求得所有解。

单个解向量

def queen(n):
    sindex=[None for i in range(n)]
    Add=[None for i in range(n)]
    Subtract=[None for i in range(n)]
    i=0
    j=0
    while i<n:
        while j<n and Violatec(i,j,sindex,Add,Subtract):
            j+=1
        if j<8:
            sindex[i]=j
            Add[i]=i+j
            Subtract[i]=i-j
            i+=1
            j=0
        else:#回溯
            i-=1
            if i<0:
                break
            j=sindex[i]+1
            sindex[i]=None
            Add[i]=None
            Subtract[i]=None
    if i>=8:
        print(sindex)
    else:
        print('Non')

def Violatec(i,j,sindex,Add,Subtract):  #判断当前添加的部分解是否违法
    return j in sindex or i+j in Add or i-j in Subtract

所有解向量

def queen(n):
    k=0
    sindex=[None for i in range(n)]
    Add=[None for i in range(n)]
    Subtract=[None for i in range(n)]
    i=0
    j=0
    while i>=0:
        while j<n and Violatec(i,j,sindex,Add,Subtract):
            j+=1
        if j<n:
            sindex[i]=j
            Add[i]=i+j
            Subtract[i]=i-j
            i+=1
            j=0
        else:#回溯
            i-=1
            if i<0:
                break
            j=sindex[i]+1
            sindex[i]=None
            Add[i]=None
            Subtract[i]=None
        if i>=n:
            k+=1
            print(sindex)
            i=n-1
            j=sindex[i]+1
            sindex[i]=None
            Add[i]=None
            Subtract[i]=None

    print('No more solution')
    print(k)
            

def Violatec(i,j,sindex,Add,Subtract):  #判断当前添加的部分解是否违法
    return j in sindex or i+j in Add or i-j in Subtract