每天给你送来NLP技术干货!
来自:ChallengeHub
A.监督学习
1.EDA(Exploratory Data Analysis)
2.K-Nearest Neighbors(KNN)
3.线性回归
4.交叉验证(CV)
5.正则化回归
6.ROC曲线与逻辑回归
7.超参数调优
8.SVM
B.无监督学习
1.Kmeans聚类
2.聚类分析
3.标准化
4.层次分析法
5.T-分布随机近邻嵌入(T - SNE)
6.主成分分析(PCA)
A.监督学习
监督学习: 使用有标签的数据。例如,骨科患者数据中有正常和不正常的标记。
有特征和目标变量。特征变量像骨盆桡骨或骶骨斜坡,目标变量是标签正常和异常
目的是根据给定的特征(输入)预测目标变量(输出)是正常还是异常
分类:目标变量由正常或异常等类别组成
回归:目标变量像股票市场一样是连续的
1.EDA
我总是从head()开始查看骨盆发生率、骨盆倾斜数值、腰椎前凸角、骶骨倾角、骨盆半径和脊椎滑溜度以及目标变量class
我常用的数据信息分析还有df.shape(), df.info()等

pd.plotting.scatter_matrix:
green: normal and red: abnormal
c: color
figsize: figure size
diagonal: histohram of each features
alpha: opacity
s: size of marker
marker: marker type
color_list = ['red' if i=='Abnormal' else 'green' for i in data.loc[:,'class']]
pd.plotting.scatter_matrix(data.loc[:, data.columns != 'class'],
c=color_list,
figsize= [15,15],
diagonal='hist',
alpha=0.5,
s = 200,
marker = '*',
edgecolor= "black")
plt.show()
散点矩阵中,每个特征之间是有关系的,有多少正常(绿色)和异常(红色)类别存在。
sns.countplot(x="class", data=data)
data.loc[:,'class'].value_counts()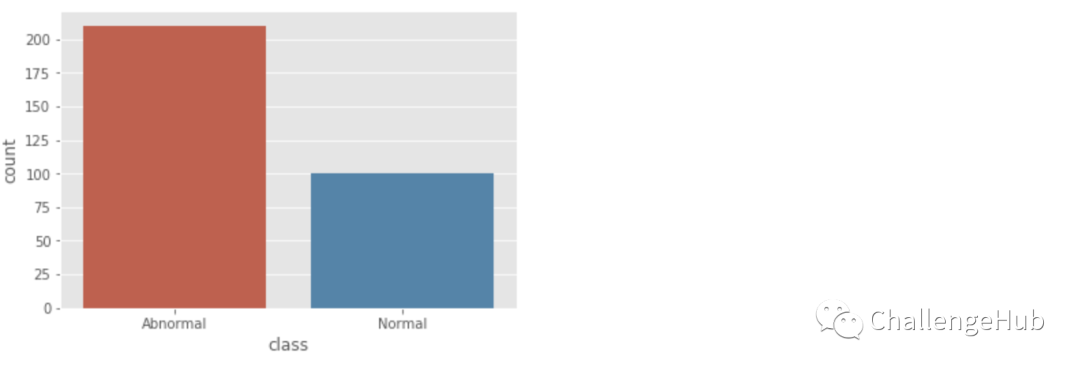
这个数据看起来是平衡的。实际上平衡数据没有具体定义,但这个数据对我们来说已经足够平衡了。现在我们来学习第一种分类方法KNN
2.KNN
# KNN
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors = 3)
x,y = data.loc[:,data.columns != 'class'], data.loc[:,'class']
knn.fit(x,y)
prediction = knn.predict(x)
print('Prediction: {}'.format(prediction))上面完成了KNN的训练和预测;
但是,我们的预测是正确的还是错误的,我们的精确度是多少,精确度是评估结果的最佳指标,不平衡数据AUC、F1-score是合适的指标,测量模型的性能,
为了评估模型, 我们需要分割数据分别为训练集和测试集:
# train test split
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.3,random_state = 1)
knn = KNeighborsClassifier(n_neighbors = 3)
x,y = data.loc[:,data.columns != 'class'], data.loc[:,'class']
knn.fit(x_train,y_train)
prediction = knn.predict(x_test)
#print('Prediction: {}'.format(prediction))
print('With KNN (K=3) accuracy is: ',knn.score(x_test,y_test)) # accuracy对于K的选择,需要考虑到模型复杂度问题:
K被称为超参数
如果K很小,高复杂度模型会导致过拟合。这意味着模型对训练集的记忆不能很好地预测测试集
如果K较大,低复杂度模型会导致欠拟合
在下面,我将K值从1到25,并找出每个K值的准确性。从图中可以看出,当K为1时,它记住了训练集,但对测试集(过拟合)不能给出很好的准确性。当K = 18时,模型会导致欠拟合。同样,准确性是不够的。然而,当K为18时(最佳性能),准确率最高,接近88%。
# Model complexity
neig = np.arange(1, 25)
train_accuracy = []
test_accuracy = []
# Loop over different values of k
for i, k in enumerate(neig):
# k from 1 to 25(exclude)
knn = KNeighborsClassifier(n_neighbors=k)
# Fit with knn
knn.fit(x_train,y_train)
#train accuracy
train_accuracy.append(knn.score(x_train, y_train))
# test accuracy
test_accuracy.append(knn.score(x_test, y_test))
# Plot
plt.figure(figsize=[13,8])
plt.plot(neig, test_accuracy, label = 'Testing Accuracy')
plt.plot(neig, train_accuracy, label = 'Training Accuracy')
plt.legend()
plt.title('-value VS Accuracy')
plt.xlabel('Number of Neighbors')
plt.ylabel('Accuracy')
plt.xticks(neig)
plt.savefig('graph.png')
plt.show()
print("Best accuracy is {} with K = {}".format(np.max(test_accuracy),1+test_accuracy.index(np.max(test_accuracy))))
3.线性回归
这里我们将学习线性回归和逻辑回归
这个骨科患者的数据不适合进行回归,所以我只使用两个特征,即骶骨倾斜和骨盆异常发生率:
我将骨盆异常发生率作为特征,目标是骶骨倾斜
# create data1 that includes pelvic_incidence that is feature and sacral_slope that is target variable
data1 = data[data['class'] =='Abnormal']
x = np.array(data1.loc[:,'pelvic_incidence']).reshape(-1,1)
y = np.array(data1.loc[:,'sacral_slope']).reshape(-1,1)
# Scatter
plt.figure(figsize=[10,10])
plt.scatter(x=x,y=y)
plt.xlabel('pelvic_incidence')
plt.ylabel('sacral_slope')
plt.show()
现在我们有了做回归的数据。在回归问题中,目标值是连续变化的变量,如房价或斜率。让直线与这些点对齐。
线性回归
y = ax + b,其中y是target, x是特征,a是模型参数
模型a的参数是根据最小误差函数,即损失函数来选择的
在线性回归中,我们使用普通最小二乘(OLS)作为损失函数。
OLS:所有残差的和但一些正的和负的残差可以互相抵消,所以我们对残差的平方和,它被称为OLS
指标评估:使用拟合优度,即
# LinearRegression
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
# Predict space
predict_space = np.linspace(min(x), max(x)).reshape(-1,1)
# Fit
reg.fit(x,y)
# Predict
predicted = reg.predict(predict_space)
# R^2
print('R^2 score: ',reg.score(x, y))
# Plot regression line and scatter
plt.plot(predict_space, predicted, color='black', linewidth=3)
plt.scatter(x=x,y=y)
plt.xlabel('pelvic_incidence')
plt.ylabel('sacral_slope')
plt.show()R^2 score: 0.6458410481075871

4.交叉验证(CV)
在KNN方法中,我们使用train test split,随机地每次拆分都完全相同。但是,如果我们不使用随机种子,数据在每次拆分时都是不同的,根据拆分精度也会不同。因此,我们可以得出模型性能依赖于train_test_split的结论。例如,对数据进行分割、拟合和预测5次,精度分别为0.89、0.9、0.91、0.92和0.93。你使用哪种精度? 你知道下一次分裂,训练和预测的精确度是多少吗?结果是无法知道的,但如果我使用交叉验证,我可以找到可接受的准确性。
# CV
from sklearn.model_selection import cross_val_score
reg = LinearRegression()
k = 5
cv_result = cross_val_score(reg,x,y,cv=k) # uses R^2 as score
print('CV Scores: ',cv_result)
print('CV scores average: ',np.sum(cv_result)/k)--
CV Scores: [0.32924233 0.61683991 0.53117056 0.1954798 0.29299864]
CV scores average: 0.393146250288486765.正则化回归/超参数调优
当我们学习线性回归选择参数(系数),同时最小化损失函数。如果线性回归认为某一特性是重要的,那么它给出了该特性的高系数。然而,这可能会导致过拟合,就像KNN中的记忆一样。为了避免过拟合,我们使用了惩罚大系数的正则化。
岭(Ridge)回归: 第一种正则化技术。也叫做L2正则化
岭回归损失函数 = OLS + alpha * sum(parameter^2)
alpha是我们需要选择适合和预测的参数。选择类似于在KNN中选择K。alpha是我们需要选择的超参数,以获得最佳的准确性和模型复杂性。这个过程称为超参数调优
如果是alpha是0呢? 损失函数= OLS,即线性修正
如果alpha很小,就会导致过拟合
如果alpha很大,就会导致欠拟合。
Lasso回归:第二种正则化技术,也叫做L1正则化
Lasso回归损失函数 = OLS + alpha * sum(absolute_value(parameter))
它可以用来选择数据中的重要特征,因为特征的值没有缩小到零,从而被Lasso回归选择
为了选择特征,我在Lasso回归数据中添加了新的特征
# Ridge
from sklearn.linear_model import Ridge
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state = 2, test_size = 0.3)
ridge = Ridge(alpha = 0.1, normalize = True)
ridge.fit(x_train,y_train)
ridge_predict = ridge.predict(x_test)
print('Ridge score: ',ridge.score(x_test,y_test))Ridge score: 0.5608287918841997
# Lasso
from sklearn.linear_model import Lasso
x = np.array(data1.loc[:,['pelvic_incidence','pelvic_tilt numeric','lumbar_lordosis_angle','pelvic_radius']])
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state = 3, test_size = 0.3)
lasso = Lasso(alpha = 0.1, normalize = True)
lasso.fit(x_train,y_train)
ridge_predict = lasso.predict(x_test)
print('Lasso score: ',lasso.score(x_test,y_test))
print('Lasso coefficients: ',lasso.coef_)--
Lasso score: 0.9640334804327547
Lasso coefficients: [ 0.82498243 -0.7209057 0. -0. ]可以看到,骨盆发生率和骨盆倾斜是重要的特征,其他特征并不重要
现在我们来讨论准确性。是否足以进行模型选择的衡量。
例如,有一个包括95%正常和5%异常样本的数据(数据标签高度不平衡),我们的模型使用精度度量。然后我们的模型对所有样本的预测为100%正常,这样就会有准确率为95%,但对所有异常样本的分类是错误的。因此,我们需要将混淆矩阵作为不平衡数据的模型度量矩阵。
tp = true positive(20), fp = false positive(7), fn = false negative(8), tn = true negative(58)
tp = Prediction is positive(normal) and actual is positive(normal).
fp = Prediction is positive(normal) and actual is negative(abnormal).
fn = Prediction is negative(abnormal) and actual is positive(normal).
tn = Prediction is negative(abnormal) and actual is negative(abnormal)
precision = tp / (tp+fp)
recall = tp / (tp+fn)
f1 = 2 precision recall / ( precision + recall)
# Confusion matrix with random forest
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.ensemble import RandomForestClassifier
x,y = data.loc[:,data.columns != 'class'], data.loc[:,'class']
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.3,random_state = 1)
rf = RandomForestClassifier(random_state = 4)
rf.fit(x_train,y_train)
y_pred = rf.predict(x_test)
cm = confusion_matrix(y_test,y_pred)
print('Confusion matrix: \n',cm)
print('Classification report: \n',classification_report(y_test,y_pred))
# visualize with seaborn library
sns.heatmap(cm,annot=True,fmt="d")
plt.show()
6.ROC曲线与逻辑回归
逻辑回归输出是概率
如果概率高于0.5数据被标记为1(异常)否则0(正常) (这是按照默认阈值)
默认logistic回归阈值为0.5
ROC在这条曲线中,x轴是假阳性率,y轴是真阳性率
图中曲线越靠近左上角,检验就越准确。
Roc曲线得分为auc,即预测得分曲线下的计算面积,auc越接近1,拟合越好
fpr = False Positive Rate
tpr = True Positive Rate
# ROC Curve with logistic regression
from sklearn.metrics import roc_curve
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, classification_report
# abnormal = 1 and normal = 0
data['class_binary'] = [1 if i == 'Abnormal' else 0 for i in data.loc[:,'class']]
x,y = data.loc[:,(data.columns != 'class') & (data.columns != 'class_binary')], data.loc[:,'class_binary']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state=42)
logreg = LogisticRegression()
logreg.fit(x_train,y_train)
y_pred_prob = logreg.predict_proba(x_test)[:,1]
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
# Plot ROC curve
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC')
plt.show()
7.超参数调优
正如我在KNN中提到的,需要调整一些超参数
K在KNN种的参数选择
alpha在Ridge和Lasso
随机森林参数,如max_depth
线性回归参数(系数)
一些参数调优技巧
尝试不同参数的所有组合
通过观察测试集的指标表现
GridSearchCV
什么是GridSearchCV
Grid: K从1到50
GridSearchCV接受knn和grid,并进行网格搜索。它意味着所有超参数的组合,这里是K。
# grid search cross validation with 1 hyperparameter
from sklearn.model_selection import GridSearchCV
grid = {'n_neighbors': np.arange(1,50)}
knn = KNeighborsClassifier()
knn_cv = GridSearchCV(knn, grid, cv=3) # GridSearchCV
knn_cv.fit(x,y)# Fit
# Print hyperparameter
print("Tuned hyperparameter k: {}".format(knn_cv.best_params_))
print("Best score: {}".format(knn_cv.best_score_))其他带有2个超参数的网格搜索示例
第一个超参数是C:logistic回归正则化参数。
C太大,过拟合
C太小,欠拟合
第二个超参数是惩罚系数(损失函数):l1 (Lasso)或l2(Ridge)
# grid search cross validation with 2 hyperparameter
# 1. hyperparameter is C:logistic regression regularization parameter
# 2. penalty l1 or l2
# Hyperparameter grid
param_grid = {'C': np.logspace(-3, 3, 7), 'penalty': ['l1', 'l2']}
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = 0.3,random_state = 12)
logreg = LogisticRegression()
logreg_cv = GridSearchCV(logreg,param_grid,cv=3)
logreg_cv.fit(x_train,y_train)
# Print the optimal parameters and best score
print("Tuned hyperparameters : {}".format(logreg_cv.best_params_))
print("Best Accuracy: {}".format(logreg_cv.best_score_))8.SVM
# SVM, pre-process and pipeline
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
steps = [('scalar', StandardScaler()),
('SVM', SVC())]
pipeline = Pipeline(steps)
parameters = {'SVM__C':[1, 10, 100],
'SVM__gamma':[0.1, 0.01]}
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2,random_state = 1)
cv = GridSearchCV(pipeline,param_grid=parameters,cv=3)
cv.fit(x_train,y_train)
y_pred = cv.predict(x_test)
print("Accuracy: {}".format(cv.score(x_test, y_test)))
print("Tuned Model Parameters: {}".format(cv.best_params_))这是有监督部分的机器学习内容,有时间会继续更新无监督部分的机器学习内容,敬请期待。投稿或交流学习,备注:昵称-学校(公司)-方向,进入DL&NLP交流群。
方向有很多:机器学习、深度学习,python,情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦
整理不易,还望给个在看!























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








