Python递归函数

#1、计算阶乘n! = 1 x 2 x 3 x ... x n，用函数fact(n)表示，可以看出：
#fact(n) = n! = 1 * 2 * 3 * ... * (n-1) * n = (n-1)! * n = fact(n-1) * n
def fact(n):
    if n==1:
        return 1
    else:
        return(n * fact(n-1))
print(fact(5))
print(fact(6))


解决递归调用栈溢出的方法是通过尾递归优化，事实上尾递归和循环的效果是一样的，所以，把循环看成是一种特殊的尾递归函数也是可以的。

尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。

上面的fact(n)函数由于return n * fact(n - 1)引入了乘法表达式，所以就不是尾递归了。要改成尾递归方式，需要多一点代码，主要是要把每一步的乘积传入到递归函数中：

def f(n):
    return f_iter(n,1)
def f_iter(n,tmpRes):
    if n==1:
        return tmpRes
    else:
        return f_iter(n-1,n*tmpRes)

print(fact(998))
print(f(997))  #大于这个数调用会栈溢出

尾递归调用时，如果做了优化，栈不会增长，因此，无论多少次调用也不会导致栈溢出。

遗憾的是，大多数编程语言没有针对尾递归做优化，Python解释器也没有做优化，所以，即使把上面的fact(n)函数改成尾递归方式，也会导致栈溢出。

 

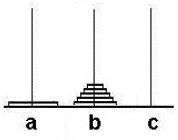
#2、汉诺塔的移动，请编写move(n, a, b, c)函数，它接收参数n，表示3个柱子A、B、C中第1个柱子A的盘子数量，然后打印出把所有盘子从A借助B移动到C的方法，

例如：

# 期待输出:
# A --> C
# A --> B
# C --> B
# A --> C
# B --> A
# B --> C
# A --> C
#move(3, 'A', 'B', 'C')

分析：将n个盘子从a全部移向c，b作为辅助柱子，此时是move（n,a,b,c）   --辅助柱子在变量中间

1）可以想象n-1个盘子从a移动到b,c作为辅助柱子      move(n-1,a,c,b)

2）然后a可将柱子最下面那个盘子移动c,      a-->c

3）此时b有n-1个盘子，将n-1个盘子从b移动到c,a作为辅助柱子，此时只是由原本的a移动到c变成了从b移动到c,重复之前的步骤，   move(n-1,b,a,c)

递归方法

def move(n,a,b,c):
    if n==1:
        print(a,' --> ',c)
        return 
    move(n-1,a,c,b)
    print(a,' --> ',c)
    move(n-1,b,a,c)

move(2, 'A', 'B', 'C')

move(3, 'A', 'B', 'C')

move(5, 'A', 'B', 'C')

A  -->  C
A  -->  B
C  -->  B
A  -->  C
B  -->  A
B  -->  C
A  -->  C
A  -->  B
C  -->  B
C  -->  A
B  -->  A
C  -->  B
A  -->  C
A  -->  B
C  -->  B
A  -->  C
B  -->  A
B  -->  C
A  -->  C
B  -->  A
C  -->  B
C  -->  A
B  -->  A
B  -->  C
A  -->  C
A  -->  B
C  -->  B
A  -->  C
B  -->  A
B  -->  C
A  -->  C