算法简述

此篇博客用于记录和整理一些重要的算法，以便自己理解和查看。

1.遗传算法

参考博客：超详细的遗传算法--程序猿声

定义：

模拟达尔文生物进化论，进行优胜劣汰、适者生存来寻找问题的最优解

袋鼠问题描述算法：

有很多袋鼠，它们降落到喜玛拉雅山脉的任意地方。目的是寻找喜马拉雅山脉最高的山峰，这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年，就在一些海拔高度较低的地方射杀一些袋鼠。于是，不断有袋鼠死于海拔较低的地方，而越是在海拔高的袋鼠越是能活得更久，也越有机会生儿育女。就这样经过许多年，这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上，可是在所有的袋鼠中，只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。

优点：

你不需要去了解和定义如何寻找出最优解，只需要每隔一段时间否定一些不符合要求的解。

不足：

不能保证一定获得最优解，就类似于人类的进化，若进化方向错了，可能在进化到最完美之前就已经灭绝。

算法图解：

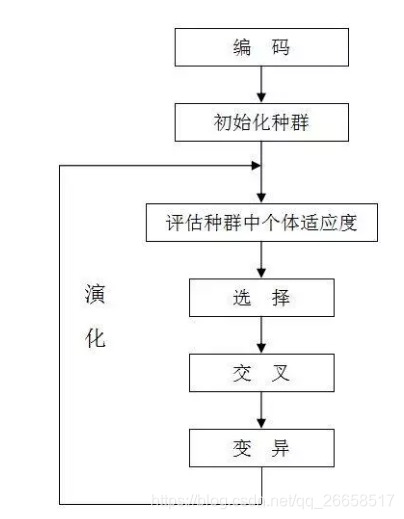
其他详细情况可进入参考博客查看或百度。