给定入栈顺序，判断出栈顺序是否合法



#include<iostream>
using namespace std;
#include<stack>
#include<cassert>
template<class T>
bool testLegal(int *stack_in, int *stack_out,size_t n)
{
	assert(stack_in&&stack_out);


	stack<T> s;
	int j = 0;//出栈数组下标
	for (size_t i = 0; i < n; i++)
	{
		s.push(stack_in[i]);
		while (!s.empty()&&s.top()==stack_out[j])
		{
			s.pop();
			++j;
		}
	}
	return (s.size() == 0) ? true : false;

}
void test1()
{
	int in[5] = { 1, 2, 3, 4, 5 };
	int out[5] = { 4, 5, 3, 2, 1 };

	cout << testLegal<int>(in, out, 5) << endl;

}

题目描述： 给定一个入栈序列，给定一个出栈序列，判断该出栈序列是否合法。

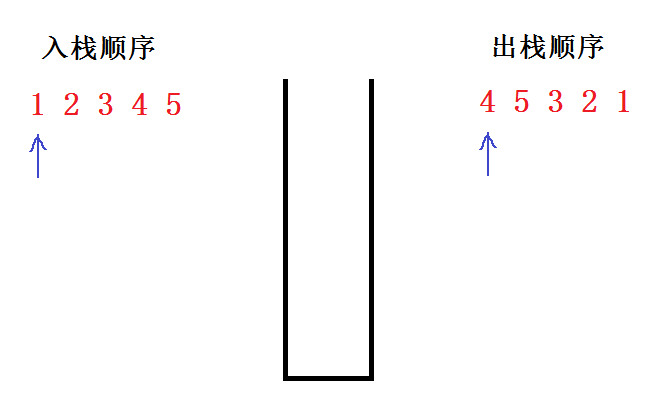
分析：假如入栈序列为1 2 3 4 5，判断4 5 3 2 1 是否是合法的出栈顺序。

两个序列均以数组的形式给出

从两个数组的第一个元素开始，如果栈为空，或者，栈顶元素不等于当前出栈数组当前下标对应的元素时，将当前入栈数组中下标所指向的元素进行压栈

初始状态如下：

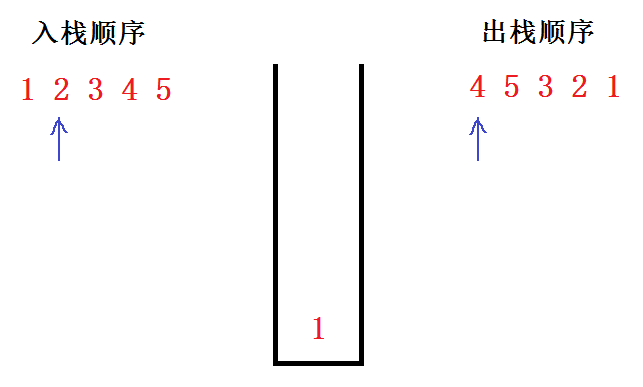
步骤1：把 1 进行压栈，并将下标后移，如下图所示，

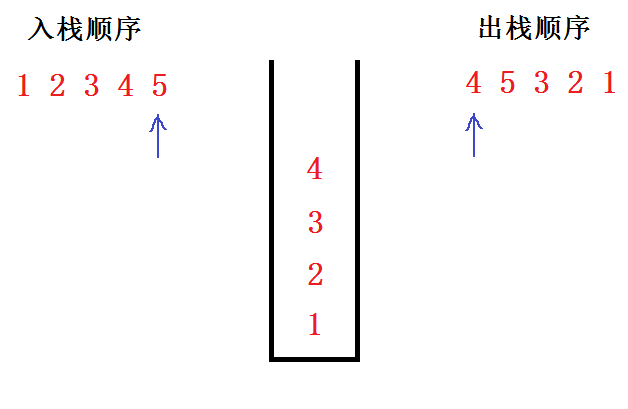
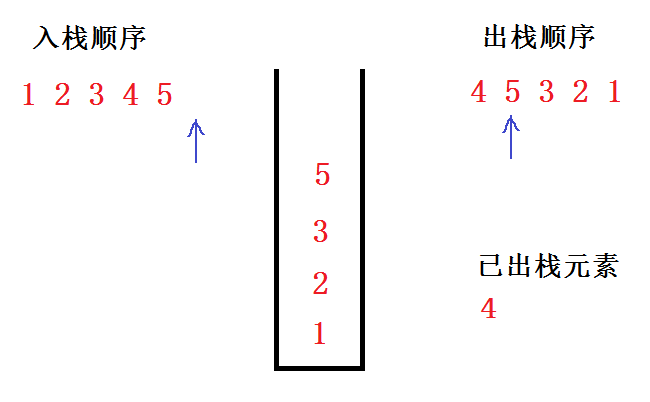
步骤2：依次进行判断并压栈，当4进栈后，此时栈顶元素等于出栈数组下标所指向的元素，将4出栈，如下图所示

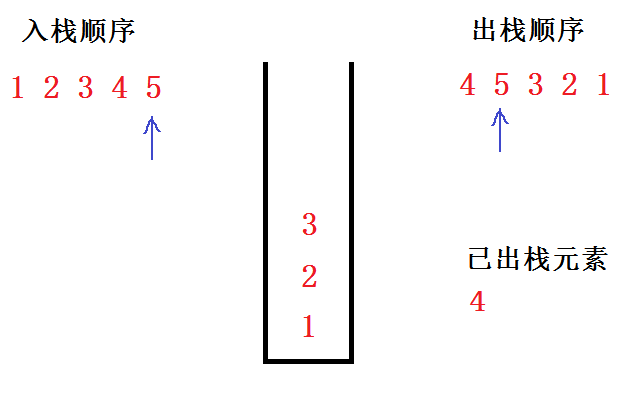
步骤3：将 4 出栈，并将出栈数组的下标后移，继续判断栈顶元素是否为当前出栈数组下标对应的元素，是，则出栈，否则继续往后执行

步骤4：重复上述步骤，直到入栈数组中的下标走到尽头

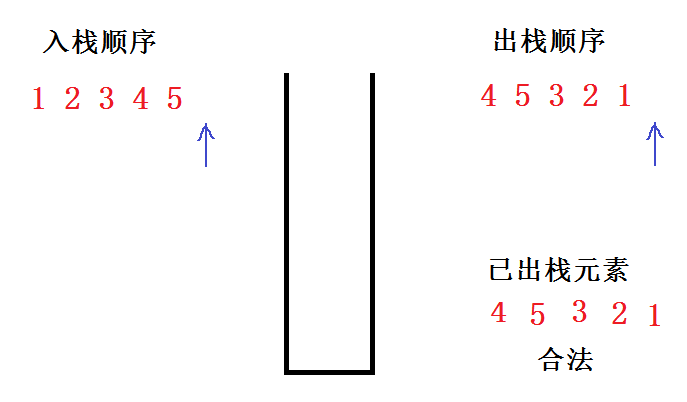
当最后一个元素入栈后，此时只需循环判断栈顶元素是否与出栈数组当前下标对应的元素相等，如果该序列合法，则栈中的元素最终都会出栈，不合法则栈永远不为空

此时，栈为空，则该序列合法。