Toy Regression
怎么样用caffe2特征实现简单的线性回归:
- 随机生成一些样本数据作为模型的输入
- 用这些数据创建一个网络
- 自动训练模型
使用SGD算法优化网络学习的参数
Browse the Tutorial
输入两维的X,一维的输出y,权重向量w=[2.0,1.5],偏置b=0.5,方程式:
y=wx+b
在本教程中,我们将使用Caffe2运算符生成训练数据。 请注意,您的日常培训工作通常不是这样:在真正场景中的训练数据通常从外部来源加载,例如Caffe DB(即键值存储)或Hive tabel。 我们将在MNIST教程中介绍。
from caffe2.python import core ,cnn, net_drawer, workspace, visualize
import numpy as np
from IPython import display
from matplotlib import pyplot声明计算图
我们声明有两个图:一个用于初始化我们将在计算中使用的不同参数和常量;另一个是使用随机梯度下降的主图。
第一,初始化网络:注意它的名字不重要,我们基本上想把初始化代码放在一个网中,所以,我们可以调用RunNetOnce()来执行它。分开初始化init_net的原因是,这些operators在训练过程中不需要运行多次。
init_net=core.Net("init")
#The ground truth parameters
W_gt=init_net.GivenTensorFill(
[],"W_gt",shape=[1,2] ,values=[2.0,1.5])
B_gt=init_net.GivenTensorFill([],"B_gt",shape=[1],values=[0.5])
#Constant value ONE is used in weighted sum when updating parameters.
ONE=init_net.ConstantFill([],"ONE",shape=[1],value=1.)
#ITER is the iterator count
ITER=init_net.ConstantFill([],"ITER",shape=[1],value=0,dtype=core.DataType.INT32)
#For the parameters to be learned: we randomly initialize weight
#from [-1,1]and init bias with 0.0.
W=init_net.UniformFill([], "W", shape=[1,2], min=-1, max=1.)
B=init_net.ConstantFill([], "B", shape=[1],value=0.0)
print("Created init net.")Created init net.训练网络定义如下:
- 前向传播计算loss
- 通过自动微分计算反向传播
- 使用标准的SGD更新参数
train_net = core.Net("train")
# First, we generate random samples of X and create the ground truth.
X = train_net.GaussianFill([], "X", shape=[64, 2], mean=0.0, std=1.0, run_once=0)
Y_gt = X.FC([W_gt, B_gt], "Y_gt")
# We add Gaussian noise to the ground truth
noise = train_net.GaussianFill([], "noise", shape=[64, 1], mean=0.0, std=1.0, run_once=0)
Y_noise = Y_gt.Add(noise, "Y_noise")
# Note that we do not need to propagate the gradients back through Y_noise,
# so we mark StopGradient to notify the auto differentiating algorithm
# to ignore this path.
Y_noise = Y_noise.StopGradient([], "Y_noise")
# Now, for the normal linear regression prediction, this is all we need.
Y_pred = X.FC([W, B], "Y_pred")
# The loss function is computed by a squared L2 distance, and then averaged
# over all items in the minibatch.
dist = train_net.SquaredL2Distance([Y_noise, Y_pred], "dist")
loss = dist.AveragedLoss([], ["loss"])看一下整个网络是什么样的。从下图中,你可以发现网络主要是四个部分组成的:
- 随机生成批次的X(GaussianFill生成X)
- 使用W_gt,B_gt和FC运算符生成Y_gt
- 使用目前的参数W和B来预测Y_pred
- 计算loss
graph=net_drawer.GetPydotGraph(train_net.Proto().op,"train",rankdir="LR")
display.Image(graph.create_png(),width=800)
与其它框架相似,caffe2允许我们自动生成梯度运算符,看一下网络模型变成什么样子:
#Get gradients for all the computation above
gradient_map=train_net.AddGradientOperators([loss])
graph = net_drawer.GetPydotGraph(train_net.Proto().op, "train", rankdir="LR")
display.Image(graph.create_png(),width=800)
一旦我们得到参数的梯度,我们将添加图的SGD部分:获取当前步骤的学习速率,然后进行参数更新。 在这个例子中,我们并不做任何花哨的东西:只是简单的SGD。
#Increment the iteration by one
train_net.Iter(ITER,ITER)
#compute the learning rate that corresponds to the iteration
LR=train_net.LearningRate(ITER,'LR",base_lr=-0.1,policy="step",stepsize=20,gamma=0.9)
# Weighted sum
train_net.WeightedSum([W, ONE, gradient_map[W], LR], W)
train_net.WeightedSum([B, ONE, gradient_map[B], LR], B)
# Let's show the graph again.
graph = net_drawer.GetPydotGraph(train_net.Proto().op, "train", rankdir="LR")
display.Image(graph.create_png(), width=800)
Now that we have created the networks ,let’s run them.
workspace.RunNetOnce(init_net)
workspace.CreateNet(train_net)看一下参数
print("Before training, W is: {}".format(workspace.FetchBlob("W")))
print("Before training, B is: {}".format(workspace.FetchBlob("B")))Results:
Before training, W is: [[-0.77634162 -0.88467366]]
Before training, B is: [ 0.]for i in range(100):
workspace.RunNet(train_net.Proto().name)看一下学习后的参数
print("After training, W is: {}".format(workspace.FetchBlob("W")))
print("After training, B is: {}".format(workspace.FetchBlob("B")))
print("Ground truth W is: {}".format(workspace.FetchBlob("W_gt")))
print("Ground truth B is: {}".format(workspace.FetchBlob("B_gt")))Results:
After training, W is: [[ 1.95769441 1.47348857]]
After training, B is: [ 0.45236012]
Ground truth W is: [[ 2. 1.5]]
Ground truth B is: [ 0.5]
看起来很简单吧? 我们来仔细看看参数更新在训练步骤中的进展情况。 为此,让我们重新初始化参数,并查看步骤中参数的更改。 记住我们可以随时从工作区获取Blob。
workspace.RunNetOnce(init_net)
w_history=[]
b_history=[]
for i in range(50):
workspace.RunNet(train_net.Proto().name)
w_history.append(workspace.FetchBlob("W"))
b_history.append(workspace.FetchBlob("B"))
w_history=np.vstack(w_history)
b_history = np.vstack(b_history)
pyplot.plot(w_history[:, 0], w_history[:, 1], 'r')
pyplot.axis('equal')
pyplot.xlabel('w_0')
pyplot.ylabel('w_1')
pyplot.grid(True)
pyplot.figure()
pyplot.plot(b_history)
pyplot.xlabel('iter')
pyplot.ylabel('b')
pyplot.grid(True)
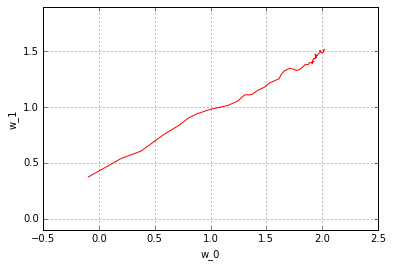
您可以观察随机梯度下降的非常典型的行为:由于噪音在整个训练过程中波动很大。 尝试多次运行上述ipython笔记本程序块 - 您将看到不同的初始化和不同噪音对结果的影响。
这只是一牛刀小试,在MNIST例子中展示真正的神经网络训练。





 本文通过Caffe2框架实现了一个简单的线性回归模型,包括生成样本数据、搭建网络结构、训练模型并使用SGD优化参数等过程。展示了如何使用Caffe2运算符进行模型训练。
本文通过Caffe2框架实现了一个简单的线性回归模型,包括生成样本数据、搭建网络结构、训练模型并使用SGD优化参数等过程。展示了如何使用Caffe2运算符进行模型训练。
















 1293
1293


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







