导论:
物理传播光学(POP)不仅可以用于简单系统,也可以设计优化复杂的光学系统,比如透镜阵列。
设计流程:
透镜阵列建模
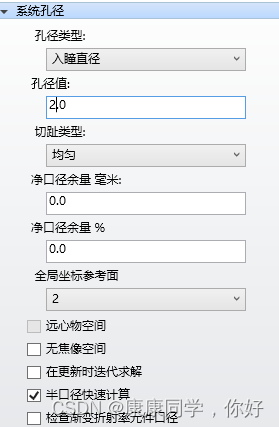
在孔径类型中选择“入瞳直径”,并输入2
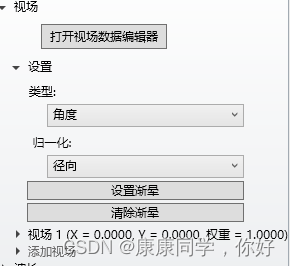
在视场设定中。设置一个视场(0视场),选择“角度”
在波长对话框中选择一个0.55um波长,如下图:
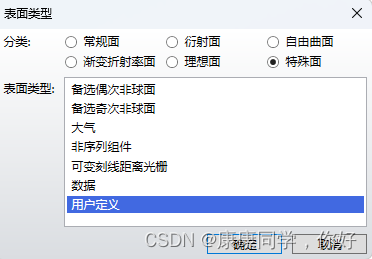
然后再镜头数据编辑器中输入光源的结构参数,如下图:

其中,第二面中选择用户自定义;
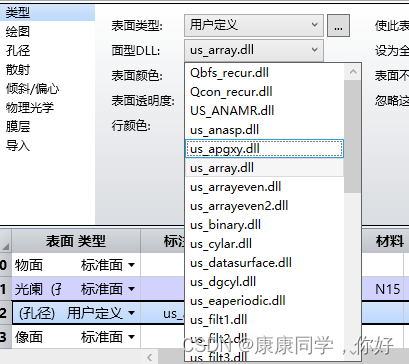
返回镜头数据编辑器,在第2面中填入透镜阵列的各个参数。

再双击第2面,在孔径对话框中选择矩形孔径,在X半宽和Y半宽中输入1.75。
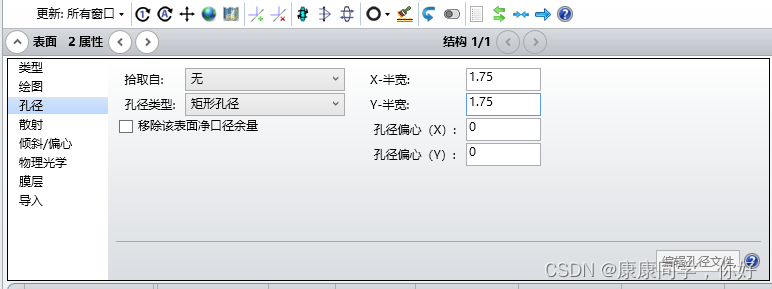
第一面也选择矩形孔径输入1.75。
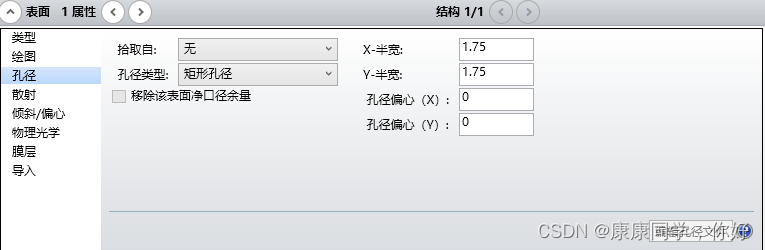
查看透镜的矢高图
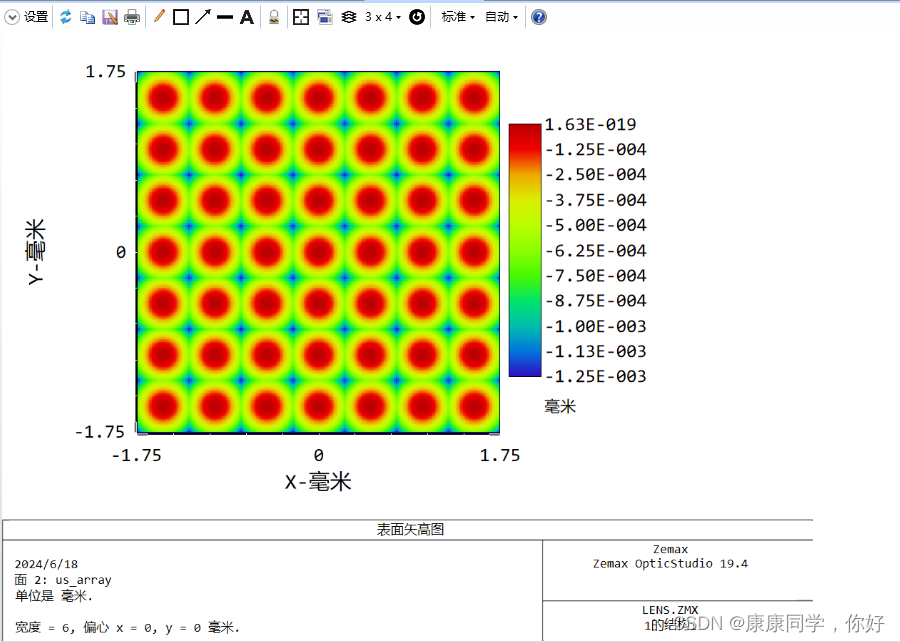
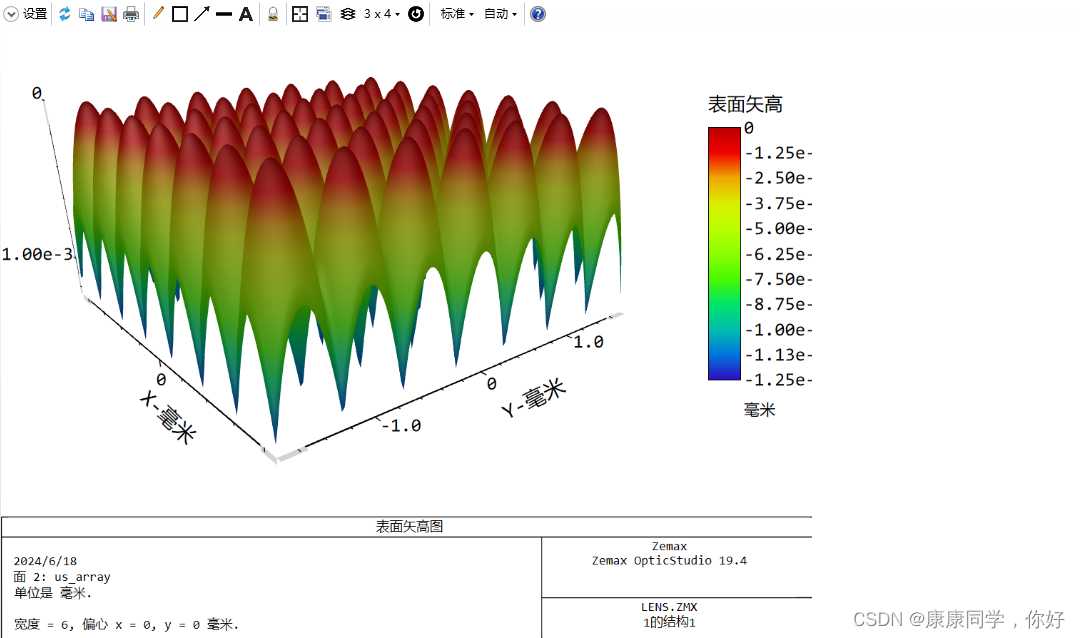
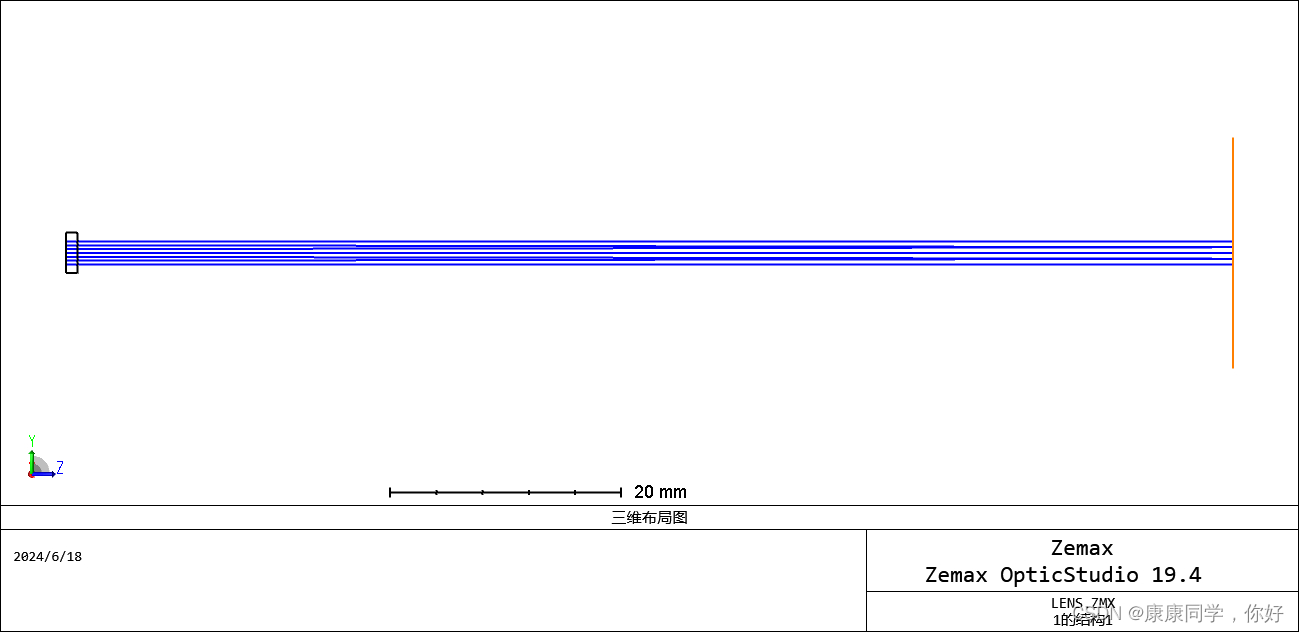
此时,系统的三维结构图,如下图:
查看POP
打开POP,查看经过透镜阵列后的光学图像。如下图
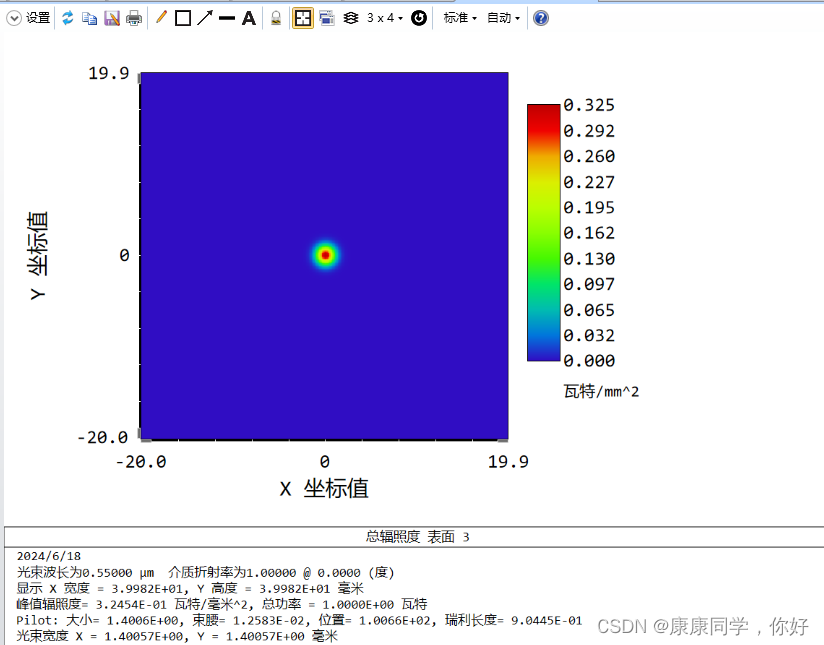





















 1万+
1万+










