目录
叙述
若 是奇质数且
是奇质数且 不能整除
不能整除 ,则:
,则:
-
 是模
是模
 的二次剩余
当且仅当:
的二次剩余
当且仅当:
-
 是模
是模
 的非二次剩余当且仅当:
的非二次剩余当且仅当:
以勒让德符号表示,即为: 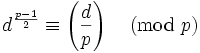
举例
例子一:对于给定数,寻找其为二次剩余的模数
令a = 17。对于怎样的质数p,17是模p的二次剩余呢?
根据判别法里给出的准则,我们可以从小的质数开始检验。
首先测试p = 3。我们有:17(3 − 1)/2 = 171 ≡ 2 (mod 3) ≡ -1 (mod 3),因此17不是模3的二次剩余。
再来测试p = 13。我们有:17(13 − 1)/2 = 176 ≡ 1 (mod 13),因此17是模13的二次剩余。实际上我们有:17 ≡ 4 (mod 13),而22 = 4.
运用同余性质和勒让德符号可以加快检验速度。继续算下去,可以得到:
-
对于质数
p =
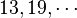 ,(17/
p) = +1(也就是说17是模这些质数的二次剩余)。
,(17/
p) = +1(也就是说17是模这些质数的二次剩余)。
-
对于质数
p =
 ,(17/
p) = -1(也就是说17是模这些质数的
二次非剩余)。
,(17/
p) = -1(也就是说17是模这些质数的
二次非剩余)。
例子二:对指定的质数p,寻找其二次剩余
哪些数是模17的二次剩余?
我们可以手工计算:
- 1 2 = 1
- 2 2 = 4
- 3 2 = 9
- 4 2 = 16
- 5 2 = 25 ≡ 8 (mod 17)
- 6 2 = 36 ≡ 2 (mod 17)
- 7 2 = 49 ≡ 15 (mod 17)
- 8 2 = 64 ≡ 13 (mod 17)
于是得到:所有模17的二次剩余的集合是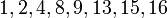 。要注意的是我们只需要算到8,因为9=17-8,9的平方与8的平方模17是同余的:92 = (−8)2 = 82 ≡ 13 (mod 17).(同理不需计算比9大的数)。
。要注意的是我们只需要算到8,因为9=17-8,9的平方与8的平方模17是同余的:92 = (−8)2 = 82 ≡ 13 (mod 17).(同理不需计算比9大的数)。
但是对于验证一个数是不是模17的二次剩余,就不必将所有模17的二次剩余全部算出。比如说要检验数字3是否是模17的二次剩余,只需要计算3(17 − 1)/2 = 38 ≡ 812 ≡ ( − 4)2 ≡ − 1 (mod 17),然后由欧拉准则判定3不是模17的二次剩余。
欧拉准则与高斯引理以及二次互反律有关,并且在定义欧拉-雅可比伪素数(见伪素数)时会用到。
证明
首先,由于 是一个奇素数,由费马小定理,
是一个奇素数,由费马小定理, 。但是
。但是 是一个偶数,所以有
是一个偶数,所以有
 是一个素数,所以
是一个素数,所以 和
和  中必有一个是
中必有一个是 的倍数。因此
的倍数。因此 模
模 的余数必然是1或-1。
的余数必然是1或-1。
- 证明若
 是模
是模 的二次剩余,则
的二次剩余,则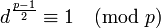
- 证明若
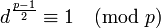 ,则
,则 是模
是模 的二次剩余
的二次剩余
 是一个奇素数,所以关于
是一个奇素数,所以关于 的原根存在。设
的原根存在。设 是
是 的一个原根,则存在
的一个原根,则存在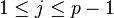 使得
使得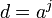 。于是
。于是
 是
是
 的一个
原根,因此
的一个
原根,因此
 模
模
 的指数是
的指数是
 ,于是
,于是
 整除
整除
 。这说明
。这说明
 是一个偶数。令
是一个偶数。令
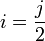 ,就有
,就有
 。
。
 是模
是模





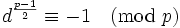
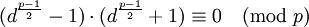
 ,
,
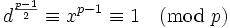
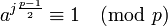
















 2738
2738

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








