正则化

最新推荐文章于 2025-09-11 17:07:53 发布

翻译最新推荐文章于 2025-09-11 17:07:53 发布 · 579 阅读

机器学习专栏收录该内容

13 篇文章

订阅专栏

本文深入探讨了L1和L2正则化在机器学习中的应用，从贝叶斯角度解析了拉普拉斯与高斯先验的区别，以及如何避免过拟合。同时，从优化角度对比了L1与L2在解空间上的差异，解释了为何L1更倾向于产生稀疏解。

1.怎么理解L1和L2？

①从贝叶斯角度：从贝叶斯的角度来分析， 正则化是为模型参数估计增加一个先验知识，先验知识会引导损失函数最小化过程朝着约束方向迭代。 L1正则是拉普拉斯先验，L2是高斯先验。整个最优化问题可以看做是一个最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计。

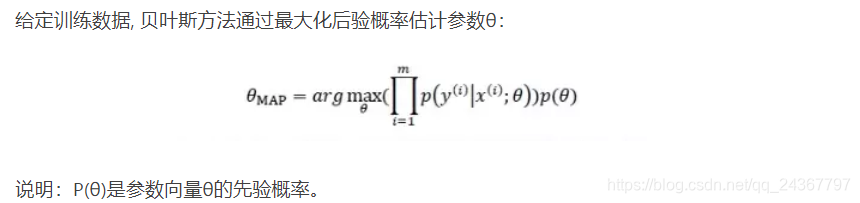
a.Ridge L2正则化

b.Lasso L1正则化

②优化角度：

“带正则项”和“带约束条件”（比如不能取过大的值）是等价的。而通过约束参数的取值空间，从而防止过拟合。因此，假设我们为上面的逻辑回归问题加一个参数的约束，比如说的范数的平方不能大于m，则我们的问题就会转为：

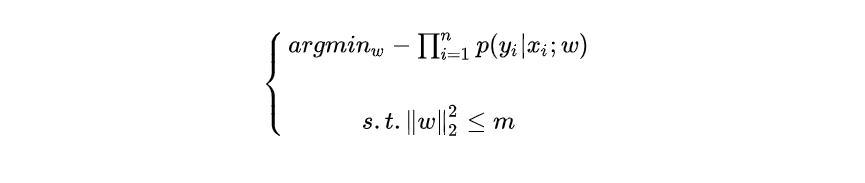
引入拉格朗日乘子的方法，因此我们就能得到：

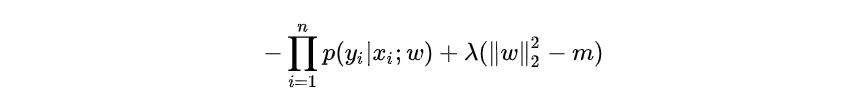
2.为什么正则化可以避免过拟合？

模型训练总是倾向于更好的拟合训练数据，包括异常样本，很显然这样的结果是模型很复杂，而且为了拟合异常样本很可能预测测试集的效果反而更差。 $\Delta$ 重点1:正则化的本质在于限制解空间。从贝叶斯角度，先验知识会引导损失函数最小化过程朝着约束方向（我的理解：概率密集方向）迭代；从优化角度，正则化等价于不等式约束。

3.为什么L1和L2效果不同？没有完全理解

①贝叶斯角度（相同分布比较0点和非0较小值的概率密度函数）

L1：参数服从拉普拉斯分布，在0处曲线有尖峰，故在0的邻域内概率密集程度远大于接近0的较小参数的概率密集程度； $\Delta$ 重点2

L2：参数服从正态分布，在0处曲线平滑，故在0的邻域和接近0的较小参数的邻域内概率密集程度相同，参数为0和参数为较小值的概率相同，因此并没有参数优化为0的趋势。

②优化角度

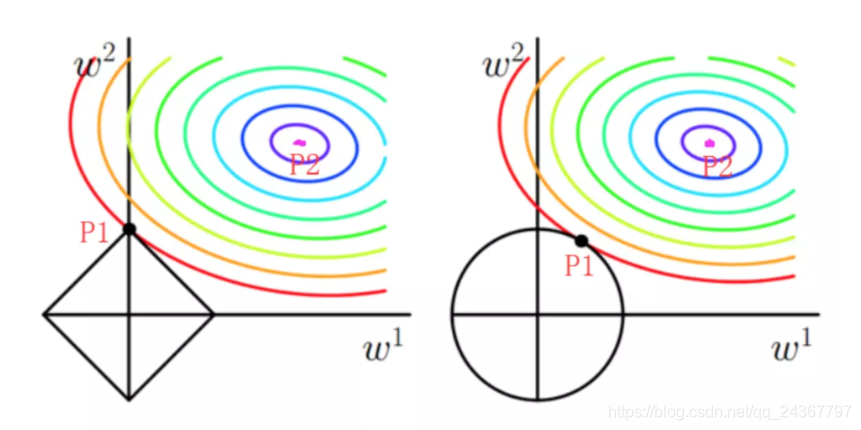
左图是L1正则项约束后的解空间（假设二维空间，简单理解为 $\omega _{1}+\omega _{2}=C$ ），右图就是L2正则项约束后的解空间（简单理解为 $\omega _{1}^{2}+\omega _{2}^{2}=R$ ）。彩色的等高线就是凸优化问题中目标函数的等高线，显然多边形的解空间更容易与等高线在交角处（顶点）碰撞出稀疏解（稀疏可以理解为，并非所有维度的参数均有值，部分参数为0，为0的话就可以理解为该维度的特征没有起到作用），而圆形的解空间，则很难在边角处碰撞，故不易产生稀疏解，更倾向于平滑的解。