自动驾驶算法—PID控制算法概述

比例-积分-微分 (PID) 控制器广泛用于控制系统，以调节过程并维持所需的设定值。它们结合了三种控制动作：比例、积分和微分，以实现精确控制和所需的性能。

一，控制系统

控制系统是一种设备或一组设备，用于管理、命令、指挥或调节其他设备或系统的行为。工业控制系统用于工业生产中控制设备或机器。

有两类常见的控制系统：

• 开环控制系统：输出仅基于输入生成。示例：假设您正在使用洗衣机，并将计时器设置为 15 分钟。现在，无论 15 分钟的洗涤后衣服是否仍然脏，机器都会在 15 分钟后停止。在这里，我们看到了衣服的数量和脏污程度，我们估计了机器的使用时间限制并进行了设置。因此，准确性取决于用户的经验。这类似于开环控制系统的运行方式。因此，输出仅基于输入生成。该系统是近似的，通常不准确。

• 闭环控制系统：考虑当前输出并根据反馈进行修正。示例：以开环系统为例，如果我们有一台洗衣机，它每时每刻都会检查衣服有多脏，并且只在衣服洗完后自动停止，而不管洗衣服需要多长时间，那么这台洗衣机就可以作为闭环控制系统运行。该系统非常准确，根据当前瞬时值判断结果，并使用反馈机制进行修正。

  

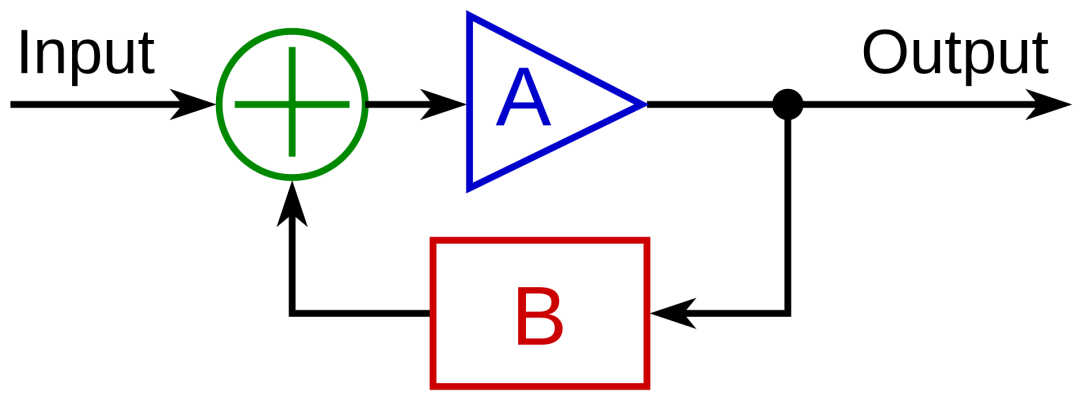
        简单控制回路

闭环系统又称反馈控制系统。人体是一个典型的反馈系统。

二，PI控制系统

2.1 PID控制器

PID 控制器或比例-积分-微分控制器是一种广泛用于工业控制系统的控制环反馈机制（控制器）。

PID 控制是工业中最常用的控制算法，在工业控制中得到普遍认可。PID 控制器之所以受欢迎，部分原因在于它在各种运行条件下都具有强大的性能，部分原因在于它功能简单，工程师可以简单直接地操作它。

PID 控制器计算误差值，即测量到的过程变量与期望设定点（期望结果）之间的差值。控制器试图通过使用操纵变量来调整过程，以最小化误差。

PID 控制器算法涉及三个独立的常数参数，因此有时也称为三项控制：

• 比例（ P）

• 积分（I）

• 导数（D）

简而言之，这些值可以根据时间来解释：“P”取决于当前误差，“I”取决于过去误差的累积，“D”是基于当前变化率对未来误差的预测。这三个动作的加权和用于通过控制元件（例如控制阀的位置、阻尼器或提供给加热元件的功率）来调整过程。

2.2 术语

理解PID需要的基本术语是：

• 误差：误差是指设备未正确执行某项操作的量。例如，假设机器人位于 x=5，但它应该位于 x=7，则误差为 2。

• 比例（P）：比例项与当前的误差成正比。

• 积分（I）：积分项取决于一段时间（t）内的累积误差。

• 导数（D）：导数项取决于误差的变化率。

• P 因子 (Kp)：用于增加或减少比例影响的常数值

• I 因子 (Ki)：用于增加或减少积分影响的常数值

• D 因子 (Kd)：用于增加或减少导数影响的常数值

注意：代码中需要调整每个项 (P、I、D)。因此，它们通过乘以相应的常数因子包含在代码中。

2.3 误差测量

为了测量与设定位置（即中心）之间的误差，我们可以使用加权值方法。假设我们使用 5 个传感器阵列来获取机器人的位置输入。可以根据可能的输入组合对获得的输入进行加权。分配的权重值应使得位置误差既精确又相对地定义。

加权值的全部范围如下所示。我们为每个值分配一个数值。

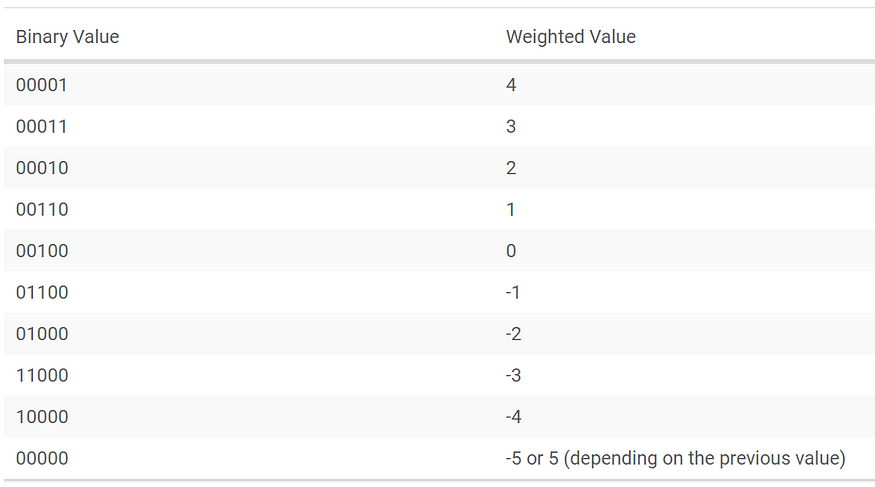
测量位置的可能值范围是 -5 到 5。我们将每秒多次测量机器人在线路上的位置，并使用这些值确定比例、积分和微分值。

2.4三个术语解释

1. 比例项：

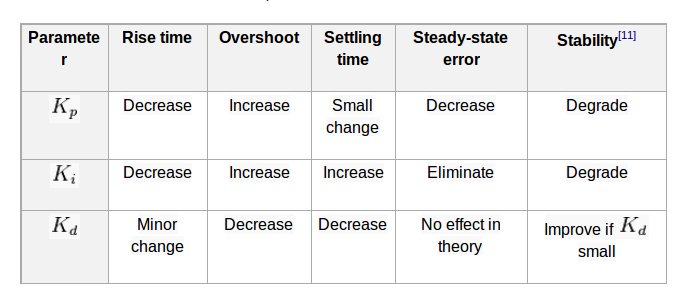
比例项产生的输出值与当前误差值成比例。简单来说，误差越大，输出值越大，因此设定值越接近（但要注意过冲和不稳定）。比例响应可以通过将误差乘以常数 Kp（称为比例增益）来调整。

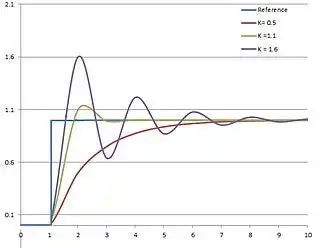
PV 与时间的关系图，针对三个 Kp 值（Ki 和 Kd 保持不变）

比例项由下式给出：

Pout = Kp*e(t)

对于给定的误差变化，高比例增益会导致输出发生较大变化。如果比例增益过高，系统可能会变得不稳定（见图）。相反，小增益会导致对大输入误差的输出响应较小，并且控制器的响应性或灵敏度较低。如果比例增益过低，则在响应系统扰动时控制动作可能太小。调节理论和工业实践表明，比例项应该对输出变化的大部分做出贡献。

2.积分项：

积分项的贡献与误差的大小和持续时间成正比。PID 控制器中的积分是瞬时误差随时间的总和，并给出应事先纠正的累积偏移（稳态误差）。然后将累积误差乘以积分增益 (Ki) 并添加到控制器输出。

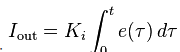
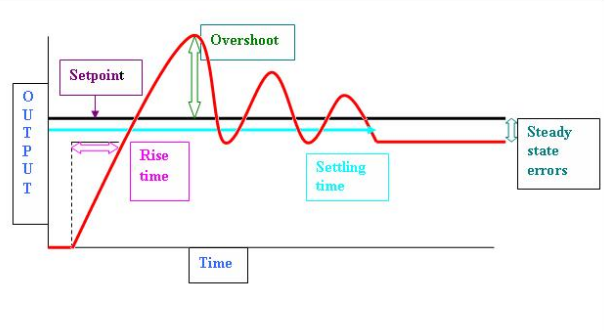
积分项加速过程向设定点移动，并消除纯比例控制器产生的残余稳态误差。然而，由于积分项响应过去累积的误差，它可能导致当前值超过设定点值（见图）。

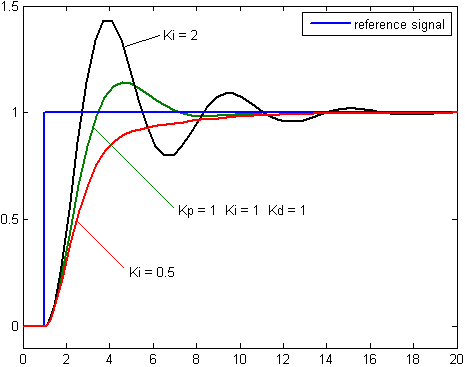
PV 与时间的关系图，针对 Ki 的三个值（Kp 和 Kd 保持不变）

积分项的主要目的是消除稳态误差。在正常情况下，会出现较小的稳态误差，积分主要用于消除该误差。然而，当误差达到 0 时，积分仍为正值，并会导致超调。超调后，积分将再次开始下降。这是积分项的负面影响。因此，总是存在权衡，您必须调整 PID 控制器以确保超调尽可能小，并最小化稳态误差。

3. 导数项：

过程误差的导数是通过确定误差随时间变化的斜率并将该变化率乘以导数增益 Kd 来计算的。导数项对整体控制作用的贡献大小称为导数增益 Kd。导数项由以下公式给出：

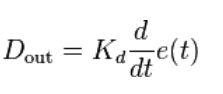
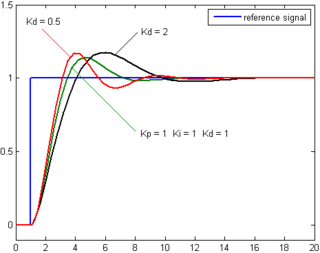
微分作用可预测系统行为，从而改善系统的稳定时间和稳定性。理想的微分不是因果关系，这意味着它非常敏感，即使有很小的噪声也会突然变化，因此 PID 控制器的实现包括对微分项的额外低通滤波，以限制高频增益和噪声。然而，微分作用在实践中很少使用——据估计，部署的控制器中只有 20% 使用了微分作用——因为它在实际应用中对系统稳定性的影响各不相同。没有微分项的 PID 控制器称为 PI 控制器。

微分项有助于最大限度地减少系统中的超调。

最终表达：

PID 控制方案以其三个校正项命名，其总和构成操纵变量 (MV)。比例、积分和微分项相加以计算 PID 控制器的输出。定义为控制器输出，PID 算法的最终形式为：

算法流程图：

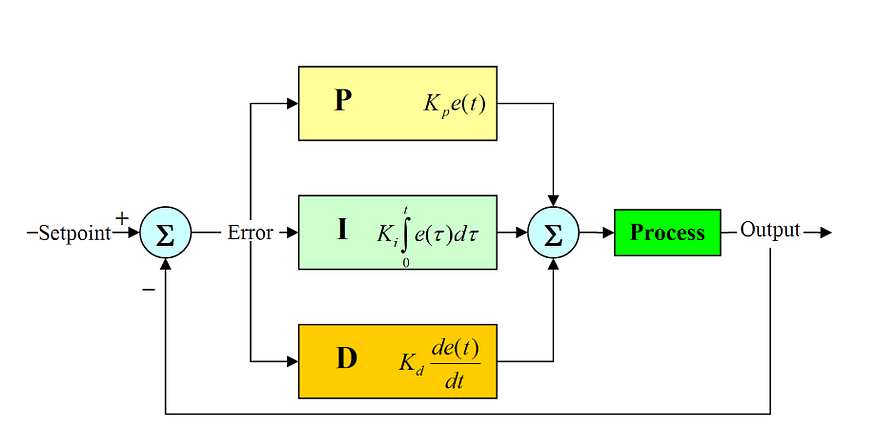
2.5一个例子

假设您正在路上行驶，并试图与前方车辆保持规定的距离 X。

比例项：如果您在 X 距离处跟随汽车，然后开始远离汽车，误差会增加，您需要按比例加速以缩小与 X 的距离。如果加速过多，您将超过 X，使距离小于 X，因此您需要减速（负误差，因此加速度为负）才能回到 X。如果减速过多，您将再次超过 X，并且需要加速才能回到 X。如果您的比例加速度不正确，这种情况将继续，这就是您在调整时看到的振荡。比例值控制纠正误差所需的努力。

积分项：积分可帮助您重新获得 X 距离并更准确地保持该距离。它考虑了所有误差并将它们累积起来。如果您落后于汽车，则误差将为正值，它将推动您前进，反之亦然。在我们的示例中，积分将使您返回到精确的 X 距离并比仅按比例加速和减速更平稳地保持该距离。如果您的汽车在 X 处并且减速带使您减速，则积分将尝试使汽车返回到 X，而如果您只有比例，它只会用比例响应进行补偿，并且永远不会真正完美地击中 X。但是积分并不完美，如果调整不当，它将慢慢偏离 X 标记。

导数项：导数用于消除积分中的累积误差。作为导数项，它作用于误差的瞬时变化，有助于平滑减速带的到来或误差的突然变化等情况。它也可能引入振荡，因为它对噪声非常敏感。在我们的例子中，您会注意到 X 距离略有增加，并防止间隙变大。导数进一步防止偏离 X 标记。由于导数容易产生噪声，因此仅在少数控制器上发现导数，并且并非完全必要。如果调整得当，它确实有助于保持汽车稳定。

手动调整：

如果系统必须保持在线，一种调整方法是首先将 Ki 和 Kd 值设置为零。增加 Kp 直到回路输出振荡，然后应将 Kp 设置为该值的大约一半，以实现“四分之一振幅衰减”型响应。然后增加 Ki 直到任何偏移在足够的时间内得到纠正。但是，Ki 太大会导致不稳定。最后，如果需要，增加 Kd，直到回路在负载扰动后能够以可接受的速度达到其参考值。但是，Kd 太大会导致响应过度和过冲。快速 PID 回路调整通常会略微过冲以更快地达到设定点；但是，有些系统无法接受过冲，在这种情况下需要过阻尼闭环系统，这将要求 Kp 设置明显小于导致振荡的 Kp 设置的一半。

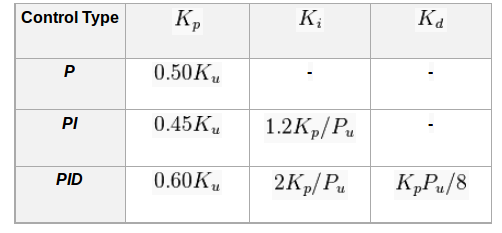
2.6 齐格勒-尼科尔斯方法：

另一种启发式调节方法正式称为 Ziegler-Nichols 方法，由 John G. Ziegler 和 Nathaniel B. Nichols 在 20 世纪 40 年代提出。与上述方法一样，和增益首先设置为零。比例增益增加，直到达到最终增益，此时环路的输出开始振荡，振荡周期用于设置增益，如下所示：

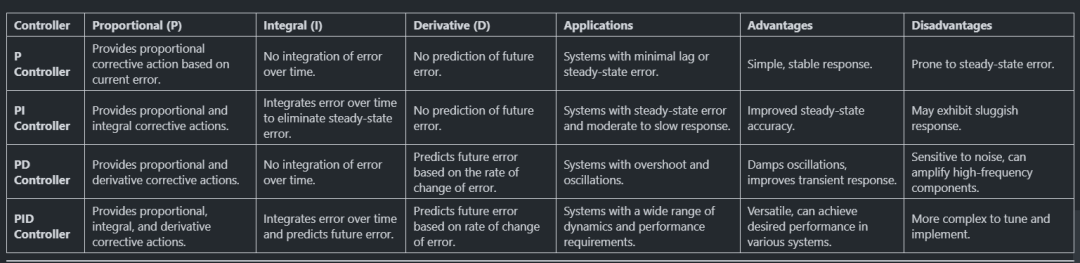
P、PI、PD 和 PID 控制器的比较：

这是一个实现 PID 控制的简单循环：

start:  error = (target_position) - (theoretical_position)  integral = integral + (error*dt)  derivative = ((error) - (previous_error))/dt  output = (Kp*error) + (Ki*integral) + (Kd*derivative)  previous_error = error  wait (dt)  goto start

三，结论

PID 控制器仅依赖于测量的过程变量，而不依赖于底层过程的知识，这使其成为一种广泛使用的控制器。通过调整 PID 控制器算法中的三个参数，控制器可以提供针对特定过程要求而设计的控制动作。控制器的响应可以用控制器对错误的响应度、控制器超过设定值的程度以及系统振荡程度来描述。请注意，使用 PID 算法进行控制并不能保证系统的最佳控制或系统稳定性。某些应用可能只需要使用一个或两个动作来提供适当的系统控制。这可以通过将其他参数设置为零来实现。如果没有相应的控制动作，PID 控制器将被称为 PI、PD、P 或 I 控制器。PI 控制器相当常见，因为微分动作对测量噪声很敏感，而没有积分项可能会阻止系统因控制动作而达到其目标值。

四，参考文献

https://medium.com/autonomous-robotics/pid-control-85596db59f35