《Introduction to Algorithm》22.4-2

最新推荐文章于 2024-09-23 14:07:37 发布

原创最新推荐文章于 2024-09-23 14:07:37 发布 · 458 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#Introduction to Algorithm #22.4-2 #算法导论

Algorithm 同时被 2 个专栏收录

14 篇文章

订阅专栏

《Introduction to Algorithm》

2 篇文章

订阅专栏

本文介绍如何利用拓扑排序与深度优先搜索（DFS）算法计算有向无环图中两点间的所有简单路径数量。通过一个具体示例，详细解释了算法的实现步骤与正确性验证。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description for 22.4-2

在这里插入图片描述

Solutions for 22.4-2

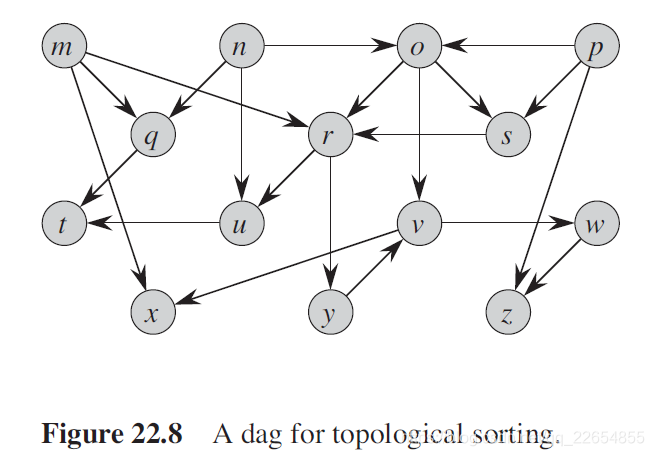
第22章第4节讲述了拓扑排序的应用，最直观的做法是先利用拓扑排序对图22.8进行DFS从而获得一个拓扑序列T，之后从t开始依次向前扫描处理直到s (利用了有向无环图中无环即无反向边的性质)

下图为其中一个拓扑排序：

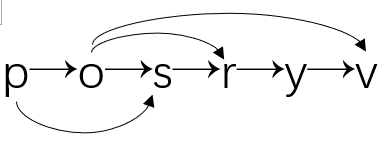
算法一 (求p到v的简单路径数)：

	1）将所有节点赋值num=0，v赋值num=1
	2）从v开始向前依次遍历，对于当前节点y：
		3）若y之前存在节点x，并且在此拓扑序列中存在边(x,y)
		4）x.num += y.num
		5）如果v==p，输出p.num

2.下面的例子方便理解，算法正确性参考DFS以及拓扑排序(有向无环图)的相关性质。考虑到时间复杂度，我们可以直接修改DFS,在拓扑序列生成前，完成对s到t的简单路径数的计算:

算法二 (DFS修改)：调用DFS(G,s)

DFS(G,s,t)
	1) for each vertex u ∈ G.V
	2) 		u.color = WHITE
	3)		u.sum = 0
	3) num = DFS-VISIT(G,s,t)
	4) return num

DFS-VISIT(G,u,t)
	1）u.color = Gray
	2) if u == t
	3) 		return 1
	4）for each v ∈ G:adj[u]
	5）		if u.color == WHITE
	6) 			sum += DFS(G,v,t)
	7) u.Color == BLACK
	8）return u.sum