面试题10:斐波那契数列
题目一:
写一个函数,输入n,求斐波那契数列的第n项。
定义:
(分段函数)
f(n)= 0 if n=0
f(n) = 1 if n=1
f(n) = f(n-1) + f(n-2) if n>1
可用递归的方式,但在递归调用层级太多时,会导致调用栈溢出,且在此题中,递归方法有很多重复的计算
使用自下而上的循环实现代码
public class Q10 {
public static void main(String[] args) {
int n = 1;
System.out.println(Fibonacci(5000));
}
public static long Fibonacci(int n) {
if(n<=1) {
return n;
}else {
long f0=0, f1=1;
long temp = 0;
for(int i=2;i<=n;i++) {
temp = f0+f1;
f0 = f1;
f1 = temp;
}
return f1;
}
}
}相关题目:
扩展:
矩形覆盖——用8个2×1的小矩形无重叠地覆盖一个2×8的大矩形,总共有多少种方法
先把2×8的覆盖方法记为f(8),用第一个1×2的小矩形去覆盖大矩形的最左边时,有两个选择(横/竖)
当竖着放时,右边还剩2×7的区域,此时记为f(7)
当横着放时:若放在左上角,则右下角必须也横着放一个1×2的小矩形,此外还剩一个2×6的区域,记为f(6)
因此f(8) = f(7) + f(6)
可看出,此时依旧是斐波那契数列

扩展部分:
1. 一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
斐波那契数列
2. 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
方法:
用f(n)表示青蛙跳上n阶台阶的跳法数,青蛙一次性跳上n阶台阶的跳法数,
f(0)=1;
当n = 1时,只有一种跳法,即1阶跳:f(1) = 1;
当n = 2时,有两种跳法,一阶跳和二阶跳:f(2) = f(1)+f(0) = 2;
当n =3时,有三种跳法,第一次跳出一阶后,后面还有f(3-1)中跳法;第一次跳出二阶后,后面还有f(3-2)中跳法;第一次跳出三阶后,后面还有f(3-3)种跳法:f(3)= f(2)+f(1)+f(0) = 4
当n= n时,共有n种跳法方式,第一次跳出一阶后,后面还有Fib(n-1)种跳法;第一次跳出二阶后,后面还有Fib(n-2)种跳法,第一次跳出n阶后,后面还有Fib(n-n)种跳法。
f(n) = f(n-1)+f(n-2)+f(n-3)+……+f(n-n)=f(0)+f(1)+f(2)+…….+f(n-1)
又因为f(n-1)=f(0)+f(1)+f(2)+……+f(n-2)
两式相减得:f(n)-f(n-1)=f(n-1) → f(n) = 2*f(n-1) n >= 2
递归等式如下:
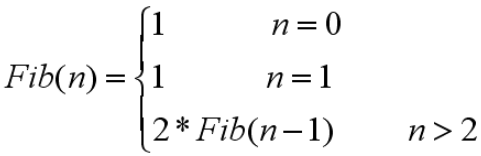





 本文深入探讨了斐波那契数列的计算方法,包括使用递归和自下而上的循环实现,并提供了Java代码示例。同时,文章扩展讨论了斐波那契数列在矩形覆盖、青蛙跳台阶等问题中的应用。
本文深入探讨了斐波那契数列的计算方法,包括使用递归和自下而上的循环实现,并提供了Java代码示例。同时,文章扩展讨论了斐波那契数列在矩形覆盖、青蛙跳台阶等问题中的应用。
















 446
446

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








