·支持向量机是一种二分类模型。基本模型是定义在特征空间上的间隔最大的线性分类器。
支持向量机的学习策略就是间隔最大化
支持向量机还包括各种核技巧,学习算法是求解凸二次优化的最优化算法
核函数表示将输入从输入空间映射到特征空间得到的特征向量之间的內积。
间隔与支持向量
给定样本集D={(x1,y1),(x2,y2),...,(xm,ym)},yiϵ{−1,+1}D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\},y_i\epsilon\{-1,+1\}D={(x1,y1),(x2,y2),...,(xm,ym)},yiϵ{−1,+1},分类的目标在样本空间上找一个划分超平面,将不同样本分开。
在样本空间中划分超平面可通过下面的线性方程来描述:
ωTx+b=0\omega^Tx+b=0ωTx+b=0
其中ω=(ω1;ω2;...;ωd)\omega=(\omega_1;\omega_2;...;\omega_d)ω=(ω1;ω2;...;ωd)为法向量,b为位移量。可将超平面表示为(ω,b)(\omega,b)(ω,b)。
空间中任意点x到超平面距离为
r=∣ωTx+b∣∣∣ω∣∣r = \frac{|\omega^Tx+b|}{||\omega||}r=∣∣ω∣∣∣ωTx+b∣
假设超平面(ω,b)(\omega,b)(ω,b)可以对样本正确分类。即
ωTxi+b⩾+1,yi=+1\omega^Tx_i+b\geqslant+1, y_i=+1ωTxi+b⩾+1,yi=+1
ωTxi+b⩽+1,yi=−1\omega^Tx_i+b\leqslant+1, y_i=-1ωTxi+b⩽+1,yi=−1
距离超平面最近的几个使得等式成立,称为支持向量。
两个异类支持向量到超平面距离之和为,也被称为间隔
γ=2∣∣ω∣∣\gamma=\frac{2}{||\omega||}γ=∣∣ω∣∣2
目标在于找到具有最大间隔的超平面,也就是使得γ\gammaγ最大的参数ω\omegaω和b
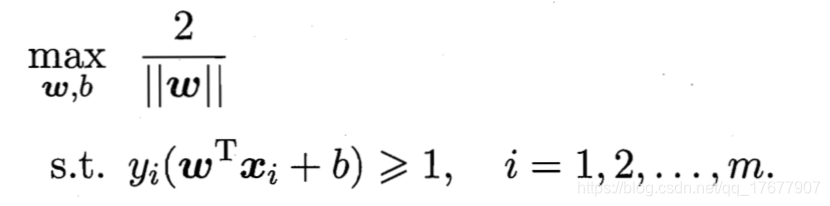
等价于最小化下面这个问题
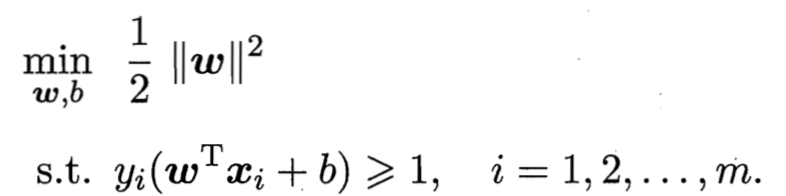
对偶问题
对上面这个式子应用拉格朗日乘子法得到其对偶问题,具体来说,对于上面每个约束都添加拉格朗日乘子αi⩾0\alpha_i\geqslant0αi⩾0,可写为
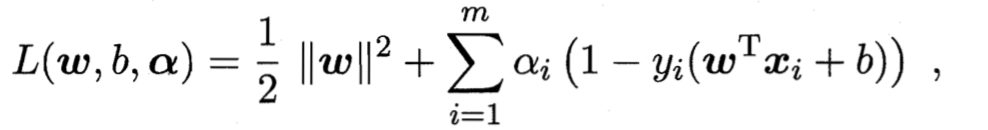
令偏导为0可得
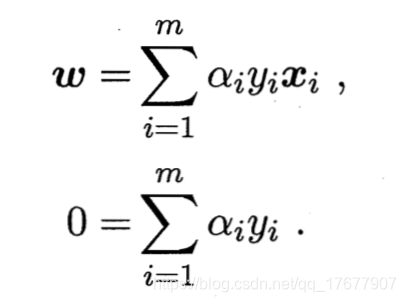
带入上一节最后公式可得其对偶问题
公式1
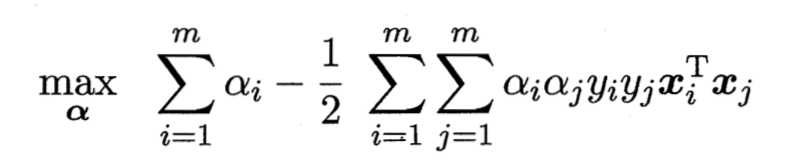
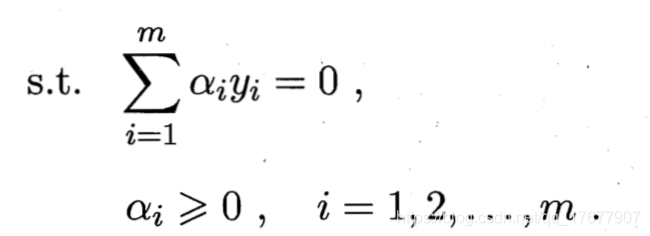
上面这个式子需要满足不等式约束的KKT条件
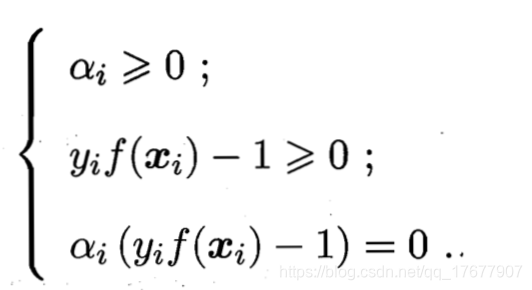
也就是αi=0\alpha_i=0αi=0和yif(xi)=1y_if(x_i)=1yif(xi)=1总有一个成立。说明训练完成后,大部分训练样本都不需要保留,模型仅与支持向量有关
下面这张图给出SVM的推导过程

SMO算法
如何求解上面这个公式呢?该问题的规模正比于训练样本数,会造成很大的开销。SMO是一种高效方法
基本思路:
- 先固定αi\alpha_iαi之外的所有参数。然后求αi\alpha_iαi上的极值
- (由于存在约束∑i=1mαiyi=0\sum_{i=1}^m\alpha_iy_i=0∑i=1mαiyi=0,若固定其他变量,αi\alpha_iαi可由其他变量计算出)
- 每次选择两个变量αi\alpha_iαi和αj\alpha_jαj并固定其他参数
- 求解公式1,获得更新后的αi\alpha_iαi和αj\alpha_jαj
- 重复上面两个步骤,直到收敛
SMO选取变量的准则:两个变量对应的样本之间的间隔最大,这样对他们的更新会给目标函数值更大的变化。
SMO算法之所以高效,因为在固定其他参数后,仅优化两个参数的过程能做到非常高效。
核函数
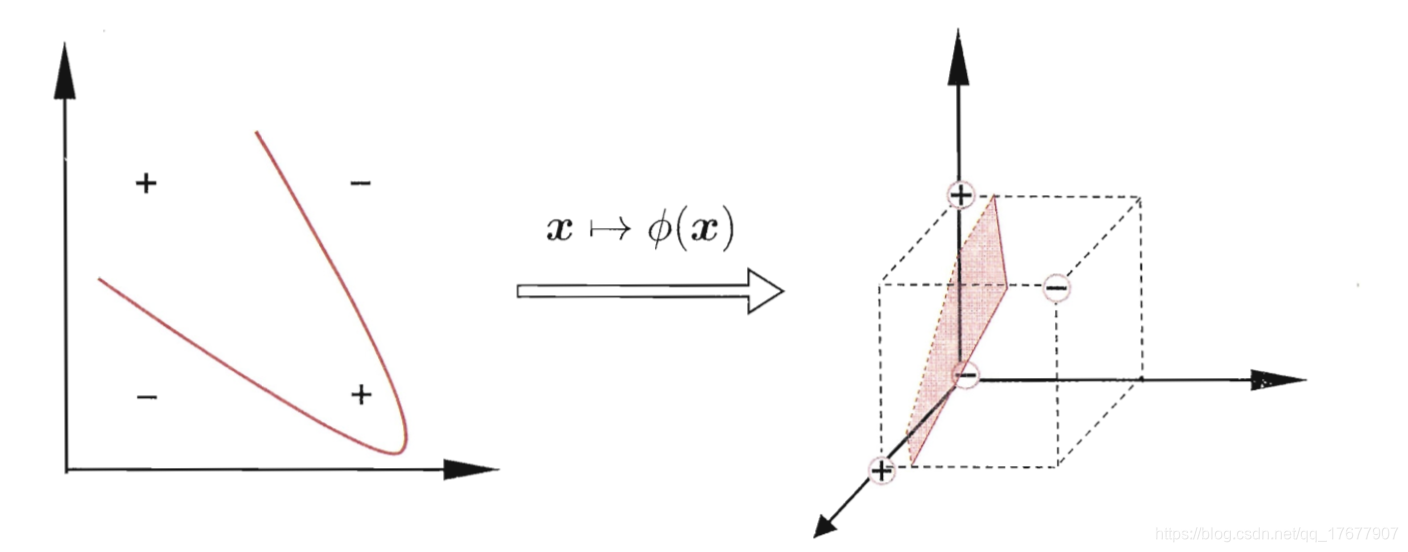
如果不存在能将类别分开的超平面,可将样本从原始空间映射到一个更高维的特征空间。

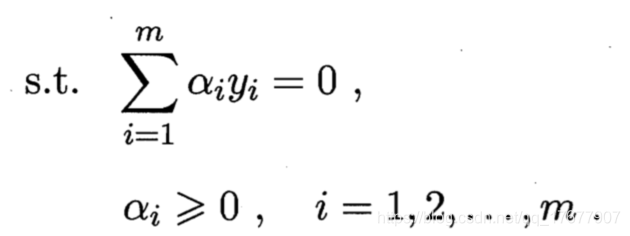
求解上面这个公式需要计算ϕ(xi)Tϕ(xj)\phi(x_i)^T\phi(x_j)ϕ(xi)Tϕ(xj)。直接计算可能很难。在此处引入核函数
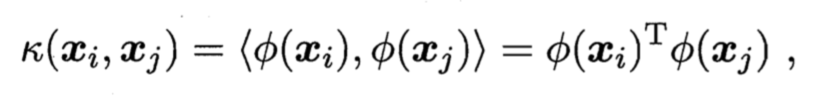
即xix_ixi与xjx_jxj在特征空间上的內积等于他们在原始空间上通过核函数k计算的结果。这样我们就可以不用计算高维空间的內积而是用核函数做映射。
那么什么样的函数可以作为核函数呢?
定理: 只要一个对称函数对应的核矩阵半正定,它就可以作为核函数。
如何选择一个合适的核函数是支持向量机最大的变数,因为核函数隐式地定义了一个特征空间
下面介绍常见的核函数

此外还可以通过函数组合得到,如线性组合γ1k1+γ2k2\gamma_1k_1+\gamma_2k_2γ1k1+γ2k2等得到
软间隔与正则化
之前的假设是存在一个超平面将所有不同类别的样本完全划分开,这种称为硬间隔。
现实情况下往往很难确定合适核函数使得线性可分。即使线性可分,也不能确定是否过拟合导致。
缓解该问题的方法是允许支持向量机在一些样本上出错。为此,引入"软间隔"概念。
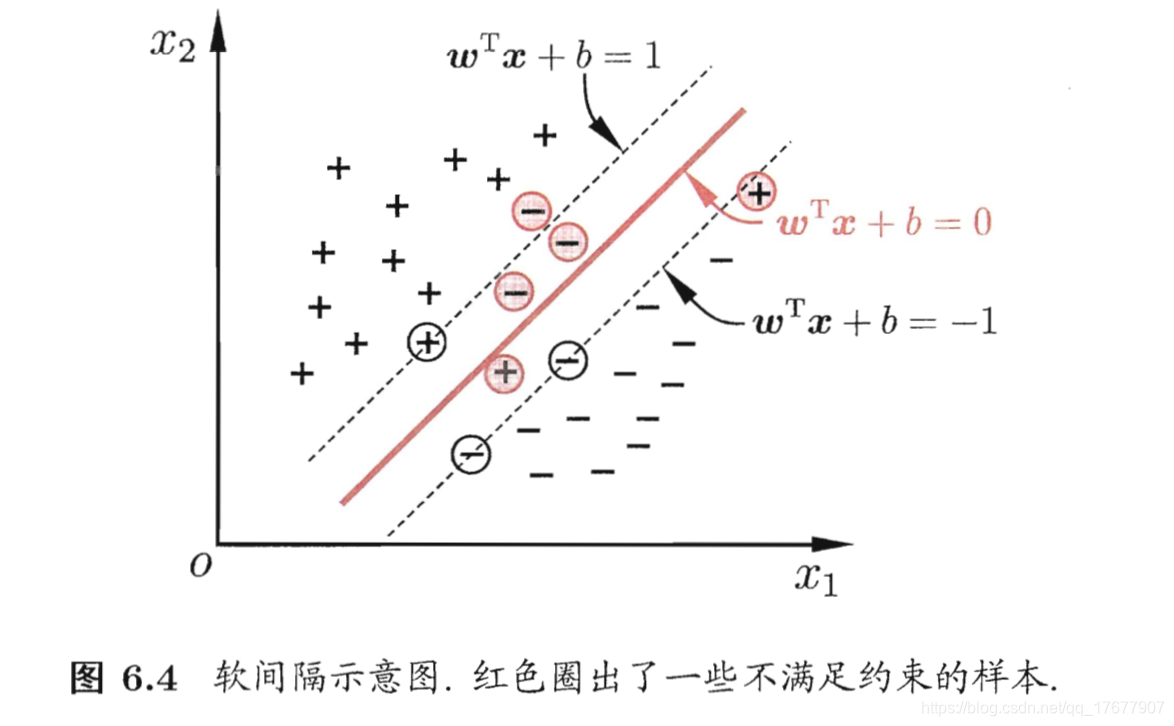
软间隔允许部分样本不满足约束
yi(ωTxi)⩾1y_i(\omega^Tx_i)\geqslant1yi(ωTxi)⩾1
当然在最大化间隔的同时,不满足约束的样本尽可能的少。于是,优化目标可以写为
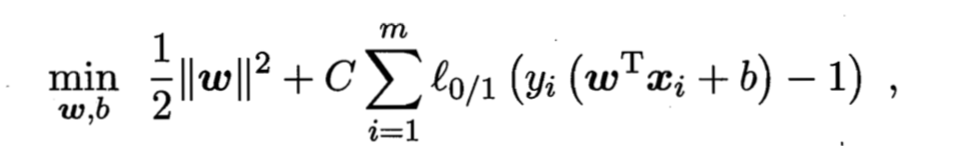
其中C是一个常数,l是0/1损失函数
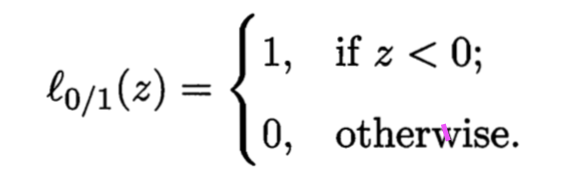
然而0/1损失函数数学性质不友好,不易于求解。有一些替代函数
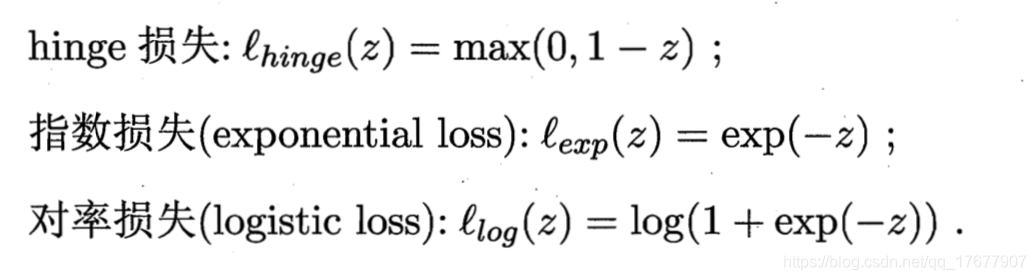
hinge损失函数
常用的损失函数是hinge损失函数,可将上面的式子重写为
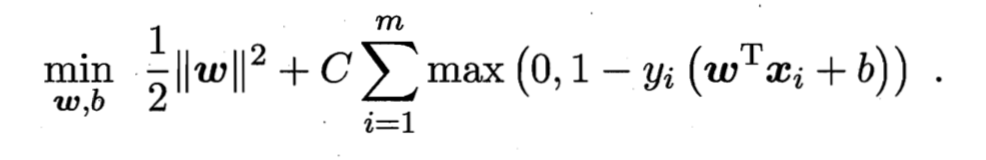
引入松弛变量ξi⩾0\xi_i\geqslant0ξi⩾0,可将上式重写为
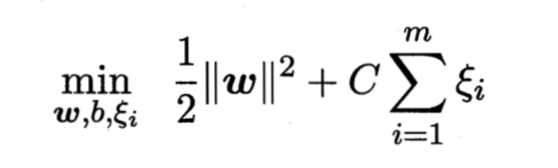
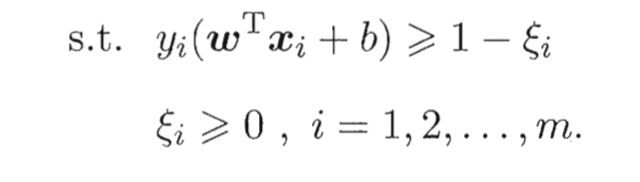
这就是常见的软间隔支持向量机
同样利用拉格朗日乘子法最后可到上式的对偶形式
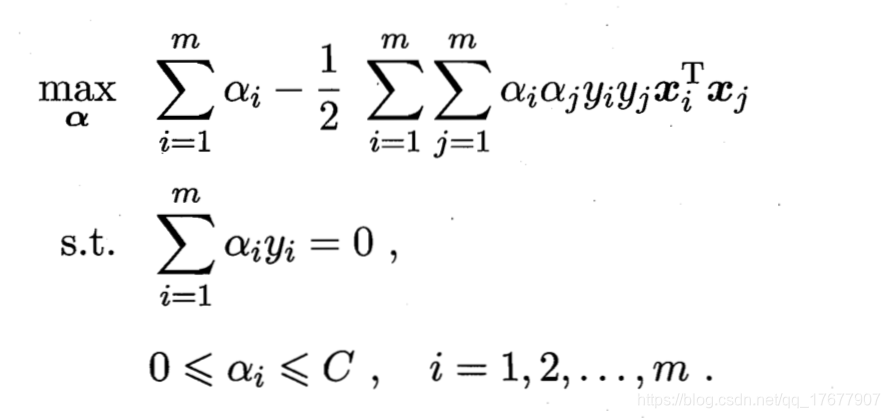
可以看到软间隔支持向量机与硬间隔支持向量机的区别在于
前者是0⩽αi⩽C0\leqslant\alpha_i\leqslant C0⩽αi⩽C,后者是0⩽αi0\leqslant\alpha_i0⩽αi





 支持向量机是一种基于间隔最大化的二分类模型,结合核函数处理非线性问题。文章介绍了对偶问题、SMO算法解决优化问题,以及软间隔在处理实际数据中的应用,通过hinge损失函数实现模型的正则化。
支持向量机是一种基于间隔最大化的二分类模型,结合核函数处理非线性问题。文章介绍了对偶问题、SMO算法解决优化问题,以及软间隔在处理实际数据中的应用,通过hinge损失函数实现模型的正则化。
















 572
572

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








