红黑树平衡原理

红黑树定义

红黑树本身也是一种二叉树，只是它是一棵平衡的二叉树，也就是两个分支均匀生长的，左右平衡的二叉树，这样的二叉树有利于内存寻址，内存寻址的时间复杂度能够做到O(logN)，我们知道数组的内存寻址时间复杂度是O(1)，只要知道数组下标就可以迅速找到数组元素的值，而链表的内存寻址时间复杂度是O(N)，寻址链表中某个元素，必须从链头元素，依次寻找链表上的全部元素，直到找到目标元素为止。红黑树内存寻址的效率是在数组和链表之间。

红黑树规则

为了红黑树两个分支均匀分布，必须设定一些规则约定红黑树的行为。

1. 每一个树节点要么黑色，要么红色
2. 根节点必须是黑色
3. 如果树节点是红色的，它的左右两个子节点必须是黑色
4. 从根到叶子节点的每条路径，包含的黑色节点数目必须相同
5. 一个节点的左子节点的关键字值小于这个节点，右子节点的关键字值大于或等于这个父节点

红黑树名词定义

根节点，左右位置节点

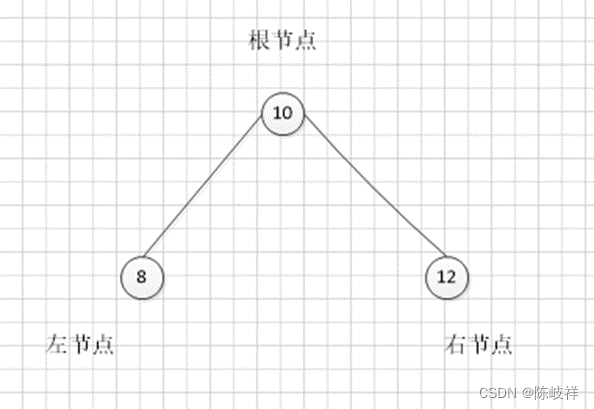
外侧子孙节点

新增节点6是左侧节点，节点8也是左侧节点，那么新增节点6就是外侧子孙节点；
新增节点14是右侧节点，节点12也是右侧节点，那么新增节点14就是外侧子孙节点。
也就是说，新增节点所在左右位置，与其父节点所在左右位置相同时，新建节点就是外侧子孙节点。

内侧子孙节点

新增节点10是右侧节点，节点8也是左侧节点，那么新增节点6就是内侧子孙节点；
新增节点11是左侧节点，节点12也是右侧节点，那么新增节点11就是内侧子孙节点。
也就是说，新增节点所在左右位置，与其父节点所在左右位置不同时，新建节点就是内侧子孙节点。

外侧子孙节点右旋转

违背红黑树规则3，节点8有左侧分支，缺失右侧分支，可以将节点6提升一级，节点8降低一级，以节点6为顶点右旋节点8。

旋转后，还是违背红黑树规则3、4，下一步修改节点颜色，使其符号红黑树规则。

经过转换后，红黑树的两个分支基本均匀分布，能够提供查找效率。

外侧子孙节点左旋转

违背红黑树规则3，节点14有右侧分支，缺失左侧分支，可以将节点14提升一级，节点12降低一级，以节点14为顶点左旋节点12。

旋转后，还是违背红黑树规则3、4，下一步修改节点颜色，使其符号红黑树规则。

内侧子孙节点右旋转

首先旋转节点12、15、16，使其成为外层子孙节点，以节点15为顶点，右旋转节点16。

再以节点15为顶点，将节点14左旋转。

由此看出：内侧子孙节点旋转需要首先转为为外层子孙节点后，再完成一次外层子孙节点旋转达到平衡树的结果。