算法简介：算法概述与算法运行时间

算法是一组完成任务的指令。任何代码片段都可以视为算法。

1. 二分查找与简单查找

二分查找是一种算法，其输入是一个有序的元素列表，如果要查找的元素包含在列表中，二分查找返回其位置；否则返回NULL。二分查找每次都检查中间的元素。

def binary_search(list, item):
low = 0
high = len(list) - 1
while low <= high
	mid = (low + high)/2
	guess = list[mid]
	if guess == item:
		return mid
	if guess > item:
		high = mid - 1
	else:
		low = mid + 1
return None 

简单查找即将元素全部遍历。

1.1 运行时间

大O表示法：一种特殊的表示法，指出算法的速度有多块。
大O表示法指的并非以秒为单位的速度。大O表示法让你能够比较操作数（需要进行多少次操作），它指出了算法运行时间的增速。

假设有10亿个元素有序排列，需要查找其中的一个元素，没查找一个元素需要消耗1毫秒，则简单查找需要11天左右，二分查找需要30ms。

就拿二分查找和简单查找来举例说明。假设这两种算法的运行时间包含如下常量。

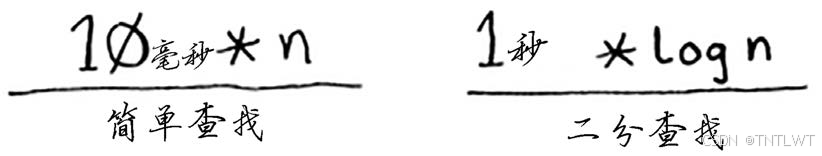
你可能认为，简单查找的常量为10毫秒，而二分查找的常量为1秒，因此简单查找的速度要快得多。现在假设你要在包含40亿个元素的列表中查找，简单查找需要463天而二分查找仅需要32秒，二分查找的速度还是快得多，常量根本没有什么影响。

假设列表有n个元素。

• 简单查找需要查找每个元素，因此需要执行n次操作，使用大O表示法，这个运行时间为O(n)。
• 二分查找需要执行log n次操作，使用大O表示为O(log n)。

2. 算法运行时间

大O表示法指出了最糟情况下的运行时间。

一些常见的大O运行时间：
O(log n)，对数时间，如二分查找
O(n)，线性时间，如简单查找
O(n*log n)，如快速排序
O(n^2)，如选择排序
O(n!)，如旅行商问题

• 算法的速度指的并非时间，而是操作数的增速。
• 谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。
• 算法的运行时间用大O表示法表示。
• O(log n)比O(n)快，当需要搜索的元素越多时，前者比后者快的越多。

3. 算法概述

算法是问题求解过程的精确描述，它为解决某一特定类型的问题规定了一个运算过程，并且具有下列特性：

1. 有穷性。一个算法必须在执行有穷步骤之后结束，且每一步都可在有穷时间内完成。
2. 确定性。算法的每一步必须是确切定义的，不能有歧义。
3. 可行性。算法应该是可行的，这意味着算法中所有要进行的运算都能够由相应的计算装置所理解和实现，并可通过有穷次运算完成。
4. 输入和输出。一个算法有零个或多个输入，它们是算法所需的初始量或被加工的对象的表示。这些输入取自特定的对象集合。一个算法必须有一个或多个输出，它们是与输入有特定关系的量。

算法是特定问题的求解方法、规则和步骤。评价一个算法从以下一个方面：

1. 正确性。输入条件能得到正确的结果。
2. 可读性。简单易懂。
3. 健壮性。也称为鲁棒性，即对非法输入的抵抗能力。
4. 效率。要求算法运行的时间短、占用空间小。

3.1 算法与数据结构

程序 = 数据结构 + 算法

程序从根本上看是解决两方面问题：对数据的描述和对操作运算的描述。在程序中需要制定数据的类型和数据的组织形式，也就是定义数据类型，描述操作的步骤就构成了算法。

设计数据类型时应当考虑可扩展性，修改数据结构会影响算法的实现。

3.2 算法效率

算法效率利用时间复杂度和空间复杂度表示。因为算法的时间消耗情况难以精确表示，所以算法分析时常采用其空间开销随n的增长趋势来表示。
空间复杂度：大O表示法。
时间复杂度：通过计算语句频度。语句频度是指语句被重复执行的次数，如某个语句在算法执行的过程中被执行n次，则其语句频度为n。这里的语句为基本语句，循环语句和函数调用语句不能作为基本语句。算法中顺序执行的各基本语句的语句频度之和表示算法的执行时间。

3.3 算法描述

常用算法的描述方法有流程图、NS盒图、伪代码和决策表等。

流程图

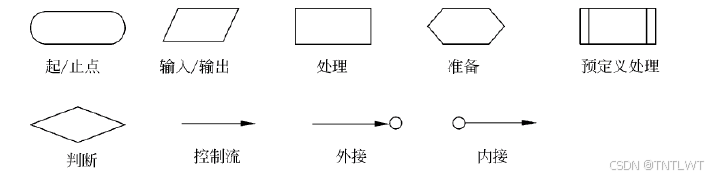
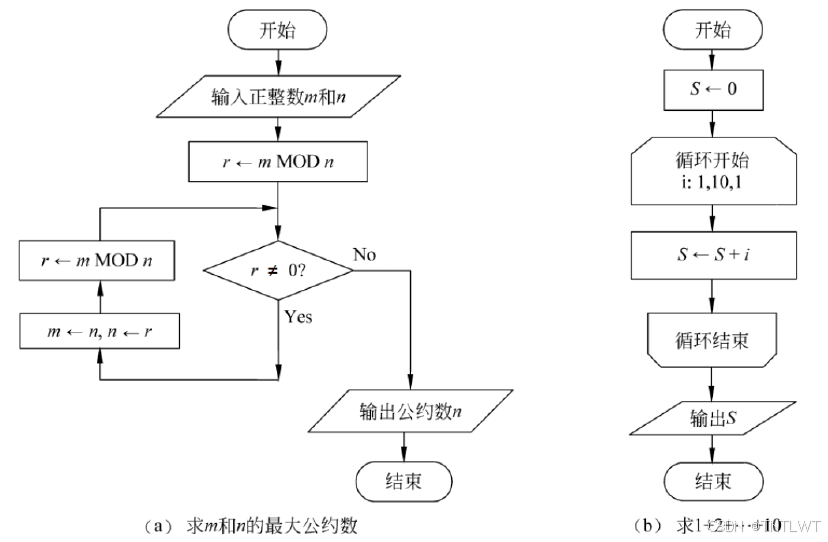
NS盒图：结构化编程描述工具

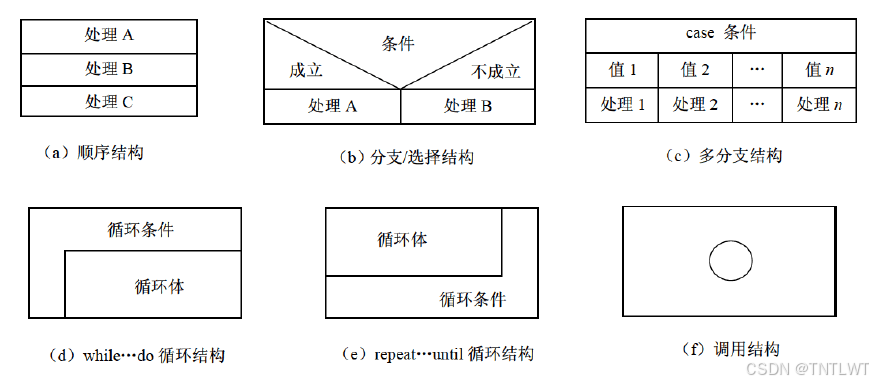
实例：求最大公约数的欧几里得算法

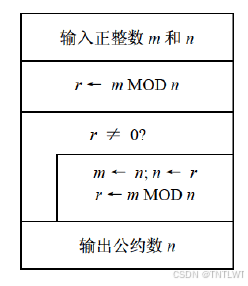
伪代码

借助程序语言的语法结构和自然语言叙述，使算法具有良好的结构又不拘泥于程序语言的限制。这样的算法易读易写，而且容易转换为程序。

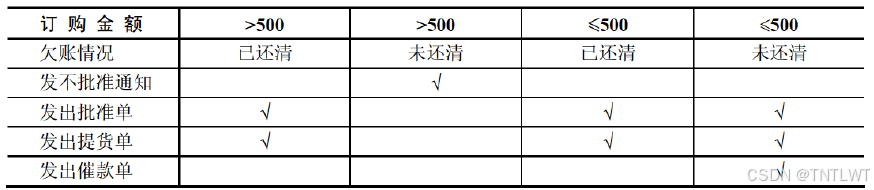
决策表

决策表将比较复杂的决策问题简洁、明确、一目了然地描述出来。