每周一算法：倍增法求最近公共祖先（LCA）

原创已于 2024-03-09 21:56:22 修改 · 1.4k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #青少年编程 #信息学竞赛 #c++

于 2024-01-05 14:04:06 首次发布

每周一算法专栏收录该内容

50 篇文章

订阅专栏

本文介绍了如何在给定的有根多叉树中使用朴素算法和倍增法解决最近公共祖先问题，包括算法原理、时间复杂度分析和C++代码实现。重点讲解了如何通过预处理和深度调整来减少查询时间。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接

【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 $N, M, S$ ，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 $N - 1$ 行每行包含两个正整数 $x, y$ ，表示 $x$ 结点和 $y$ 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 $M$ 行每行包含两个正整数 $a, b$ ，表示询问 $a$ 结点和 $b$ 结点的最近公共祖先。

输出格式

输出包含 $M$ 行，每行包含一个正整数，依次为每一个询问的结果。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $30\%$ 的数据， $N\leq 10$ ， $M\leq 10$ 。

对于 $70\%$ 的数据， $N\leq 10000$ ， $M\leq 10000$ 。

对于 $100\%$ 的数据， $\leq N,M\leq 500000$ ， $\leq x, y,a ,b \leq N$ ，不保证 $\neq b$ 。

样例说明：

该树结构如下：

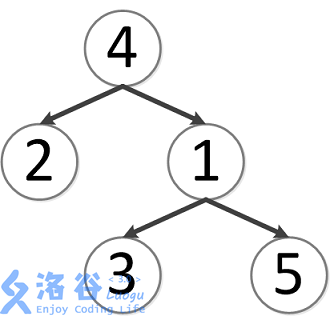
第一次询问： $2, 4$ 的最近公共祖先，故为 $4$ 。

第二次询问： $3, 2$ 的最近公共祖先，故为 $4$ 。

第三次询问： $3, 5$ 的最近公共祖先，故为 $1$ 。

第四次询问： $1, 2$ 的最近公共祖先，故为 $4$ 。

第五次询问： $4, 5$ 的最近公共祖先，故为 $4$ 。

故输出依次为 $4, 4, 1, 4, 4$ 。

算法思想

朴素算法

可以每次找深度比较大的那个点，让它向上跳。显然在树上，这两个点最后一定会相遇，相遇的位置就是想要求的 LCA。或者先向上调整深度较大的点，令他们深度相同，然后再共同向上跳转，最后也一定会相遇。

朴素算法预处理时需要 dfs 整棵树，时间复杂度为 $O (n)$ ，单次查询时间复杂度为 $O (n)$ 。如果树满足随机性质，则时间复杂度与这种随机树的期望高度有关。

倍增法

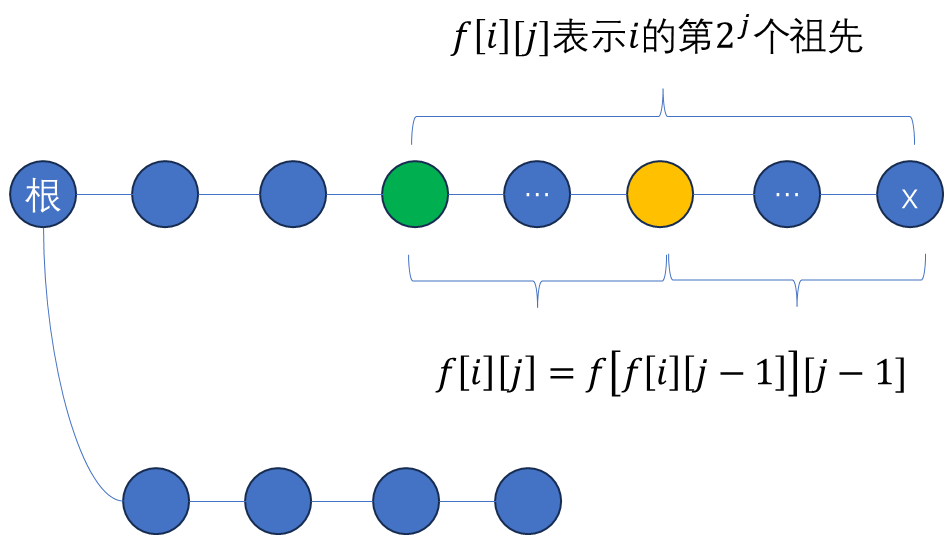
倍增算法是最经典的 LCA 求法，是朴素算法的改进算法。通过预处理 $f [i] [j]$ 数组，可以大幅减少了跳转次数。 $f [i] [j]$ 表示点 $i$ 的第 $2^j$ 个祖先。 $f [i] [j]$ 数组可以通过 dfs 预处理出来。

根据倍增思想， $f [i] [j] = f [f [i] [j - 1]] [j - 1]$ 。
在这里插入图片描述

寻找 $\text{LCA}(x,y)$ 过程可以分为两个阶段：

第一阶段中，将 $x, y$ 两点跳转到同一深度。
在第二阶段中，从最大的 $i$ 开始循环尝试，一直尝试到 $0$ （包括 $0$ ），如果 $f[x][i]\not=f[y][i]$ ，则 $x\gets f[x][i],y\gets f[y][i]$ ，那么最后的 LCA 为 $f [x] [0]$ （或 $f [y] [0]$ ）。

时间复杂度

倍增算法的预处理时间复杂度为 $\log n)$
单次查询时间复杂度为 $O(\log n)$

代码实现

#include <iostream>
#include <vector>
using namespace std;
const int N = 5e5 + 5, M = 25;
vector<int> g[N];
int depth[N], f[N][M];
void dfs(int i, int fa)
{
    depth[i] = depth[fa] + 1;
    f[i][0] = fa; //初始状态
    //计算状态f[i][j]表示从i节点开始向上2^j个祖先
    for(int j = 1; j <= 20; j ++) f[i][j] = f[f[i][j - 1]][j - 1];
    for(int j : g[i]) if(j != fa) dfs(j, i);
}
int lca(int x, int y)
{
    if(depth[x] < depth[y]) swap(x, y);
    for(int k = 20; k >= 0; k --) //从大到小枚举向上跳的距离，直到跳到和y相同的高度
    {
        if(depth[f[x][k]] >= depth[y]) x = f[x][k];
    }
    if(x == y) return x;
    for(int k = 20; k >= 0; k --)
    {
        if(f[x][k] != f[y][k]) //只要祖先节点不相等就继续向上跳
        {
            x = f[x][k], y = f[y][k];
        }
    }
    return f[x][0]; //返回x或y的父节点
}
int main()
{
    int n, m, s;
    scanf("%d%d%d", &n, &m, &s);
    for(int i = 1; i < n; i ++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        g[a].push_back(b), g[b].push_back(a);
    }
    dfs(s, 0);
    while (m -- )
    {
        int x, y;
        scanf("%d%d", &x, &y);
        int ans = lca(x, y);
        printf("%d\n", ans);
    }
}