day20|LeetCode:● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树

题目链接：654. 最大二叉树

本题思路

先放最大值在根节点，根节点把数组分成了两块，再求左右最大值互相为左子树和右子树的根结点，不断循环，到空节点结束。

一.递归法

class Solution {
private:
    // 在左闭右开区间[left, right)，构造二叉树
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left >= right) return nullptr;//终止条件

        // 分割点下标：maxValueIndex
        int maxValueIndex = left;
        for (int i = left + 1; i < right; ++i) {
            if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
        }//找下标再得到新的数组

        TreeNode* root = new TreeNode(nums[maxValueIndex]);

        // 左闭右开：[left, maxValueIndex)
        root->left = traversal(nums, left, maxValueIndex);

        // 左闭右开：[maxValueIndex + 1, right)
        root->right = traversal(nums, maxValueIndex + 1, right);

        return root;
    }
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traversal(nums, 0, nums.size());
    }
};

优化：可以把vector不用创建直接用索引代替

递归代码看代码随想录。

二：递归三部曲

1.确定返回类型和确定参数：返回头结点所以返回类型是结点型，参数为根节点

2.确定终止条件，当到达空节点时，返回空。一个叶子结点的左子树和右子树都遍历完返回叶子结点（根节点）

3.确定单层递归的逻辑，用前序遍历，因为需要先加入根节点再循环左右，return root在后面是从叶子不断返回结点组成一颗树

三.总结

1.这道题目每次都要执行三部，你就可以确定固定递归代码。

2.为什么有的递归函数需要用if疯转呢？？

第一版递归过程：（加了if判断，为了不让空节点进入递归）

if (maxValueIndex > 0) { // 这里加了判断是为了不让空节点进入递归
    vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
    node->left = constructMaximumBinaryTree(newVec);
}

if (maxValueIndex < (nums.size() - 1)) { // 这里加了判断是为了不让空节点进入递归
    vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
    node->right = constructMaximumBinaryTree(newVec);
}

第二版递归过程： （如下代码就没有加if判断）

root->left = traversal(nums, left, maxValueIndex);

root->right = traversal(nums, maxValueIndex + 1, right);

第二版代码是允许空节点进入递归，所以没有加if判断，当然终止条件也要有相应的改变。

第一版终止条件，是遇到叶子节点就终止，因为空节点不会进入递归。

第二版相应的终止条件，是遇到空节点，也就是数组区间为0，就终止了

---

题目链接：617. 合并二叉树

思考

这道题需要一次性控制两颗二叉树，我们都从同一个结点出发，遍历左子树和右子树，当左子树先没时返回右子树那个结点，后面不需要遍历是因为它相当于根节点，反之，如果都有就返回他们之和，我们以第一课数为新子树。

一.递归法（前序）

class Solution {
public:
    TreeNode*traveral(TreeNode* root1, TreeNode*root2) {
        //三种情况
        if (root1 == nullptr) return root2;
        if (root2 == nullptr) return root1;
        root1->val += root2->val;//前序
        root1->left = traveral(root1->left, root2->left);
        root1->right = traveral(root1->right, root2->right);
        return root1;//由下自上返回结点
    }
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        return traveral(root1, root2);
    }
};

二.递归三部曲

确定返回类型和参数：返回类型为新二叉树的根节点，闯入两颗树的根节点。

确定终止条件：当有一个结点为空时，如果另一个不为空，就返回这个结点，这个结点会到递归函数，这样就组成两了一颗二叉树的一半了

                         如果都为空相当于都返回空，直接到最后一行返回叶子结点。

确定单层递归的逻辑：运用前序遍历，因为一开始把第一个结点搭好，再不断创建左子树和右子树，最后return root1.不断之上返回创建，知道返回到根节点。

三.总结

1.当一个为空，另一个不为空可以返回那个不为空的，后面不需要比较吗？

因为返回那个不为空的相当于返回子树的根结点，再到递归函数确定一部分连接，最后返回局部根结点。

---

题目链接：700. 二叉搜索树中的搜索

思路

直接遍历，找到就一步步返回。哪种遍历方法都可以。

一.递归法

class Solution {
public:
    TreeNode* cur;
    void traversal(TreeNode* root, int target) {
        if (root == nullptr) return;//终止条件
        if (root->val == target) {
            cur = root;
        }//先序遍历不断查找，查到一步步返回
        traversal(root->left, target);
        traversal(root->right, target);
        
    }
    TreeNode* searchBST(TreeNode* root, int val) {
        traversal(root, val);
       return cur;
    }
};

二.递归三部曲

确定返回类型和返回条件：可以很多返回类型，这里是void，因为搜寻到了就直接返回这个全局变量。

确定终止条件：就是一个遍历，终止条件遇到空指针就返回

确定单层递归的逻辑:前序遍历，当遇到了值就可以结束遍历，这里还可以写一些剪枝。

---

题目链接：98. 验证二叉搜索树

一.插搜索树的概念

中序遍历这颗二叉树遍历结点值一依次递增，局部就是根结点大于左结点的值，小于右结点的值。

二：普通做法

可以利用性质，中序遍历二叉树，遍历过程中不断把结点加入一个容器中，最后看容器中的元素是否升序，升序就是搜索二叉树。

中序理解：遍历到哪个结点遍历完一半就可以操作它了。

class Solution {
private:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val); // 将二叉搜索树转换为有序数组
        traversal(root->right);
    }
public:
    bool isValidBST(TreeNode* root) {
        vec.clear(); // 不加这句在leetcode上也可以过，但最好加上
        traversal(root);
        for (int i = 1; i < vec.size(); i++) {
            // 注意要小于等于，搜索树里不能有相同元素
            if (vec[i] <= vec[i - 1]) return false;
        }
        return true;
    }
};

三.错误避免

陷阱一：如果不用上述的方法，写这样：对每个结点遍历，每个结点都root->left->val <= root->val && root->right->val >= root->val这样写就会出现错误，因为你这样每次只遍历了一组没有连贯性，而搜索二叉树是根结点比左子树都大，比右子树都小。如下面的情况： 

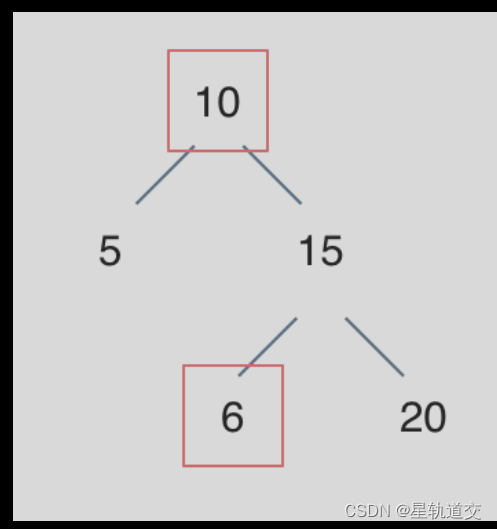
陷阱二：

因为范围是int的极限。每次都要和结点比，用一个变量，当有个别结点为int的最小时，比较结点maxval应该比它大，所以用longlong

四.递归法

class Solution {
public:
    long long maxval = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;终止条件

        bool le = isValidBST(root->left);//看左子树是不是，
        if (maxval < root->val) maxval = root->val;中序比较
        else return false;
        bool ri = isValidBST(root->right);//看右子树是不是
        return le && ri;//都是这个结点才是搜索二叉树
    }
};

五.递归三部曲

1.确定返回类型和参数类型：返回类型为bool，代表这个结点是否是搜索二叉树

2.确定终止条件：当遇到叶子结点的下一层时，因为null也可以，返回true.

3.确定单层递归的逻辑：先初始化一个最小值（比所有结点的值都小）中序遍历每个结点，如果比这个值大就更新，再比较，如果比这个值小说明就不是单调递增了，就返回false。不断向上遍历的同时需要下面结点的反馈，最后如果两边都是ture,这个结点就是true