第十一天|LeetCode:● 20. 有效的括号● 1047. 删除字符串中的所有相邻重复项● 150. 逆波兰表达式求值-优快云博客

本文探讨了如何利用栈解决括号匹配、字符串去重、逆波兰表达式求值等问题，通过C++代码实例解析思路和算法。涉及的关键概念包括栈的使用、匹配规则和递归操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：20. 有效的括号

括号匹配是使用栈解决的经典问题

1.c++代码：

class Solution {
public:
    bool isValid(string s) {
        int size = s.size();
        if (size % 2 != 0) return false;
        stack <int> st;
        for (int i = 0; i < size; i++) {
            if (s[i] == '(') {
               st.push(')'); 
            } else if (s[i] == '[') {
                st.push(']');
            } else if (s[i] == '{') {
                st.push('}');
            //第二种和第三种情况
            } else if (st.empty() || s[i] != st.top()) {
                return false;
            } else {
                st.pop();
            }
        }
       //第一种情况
       return st.empty();
    }
};

2.图像解释

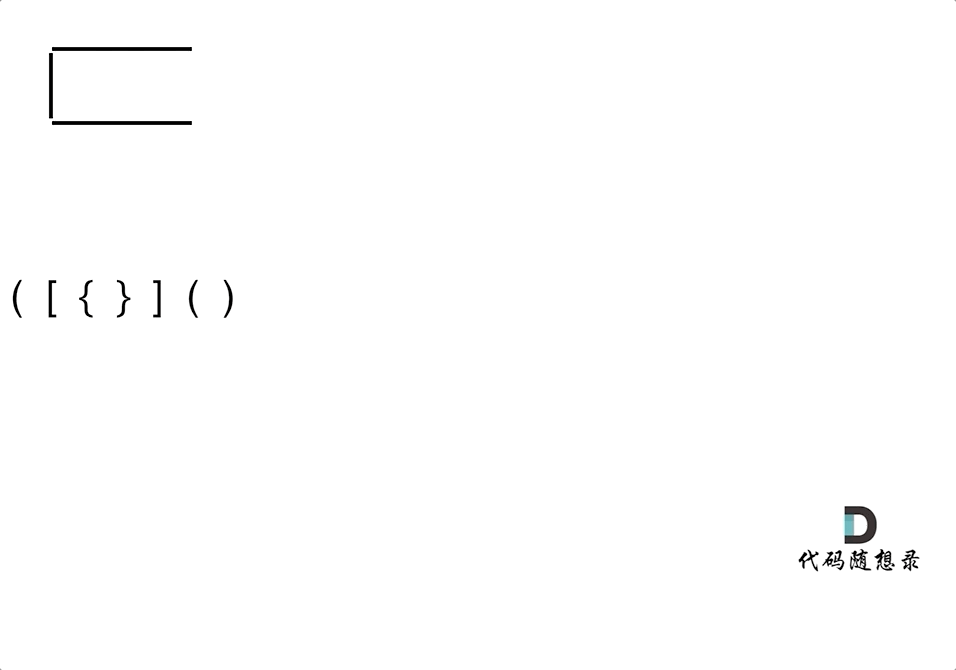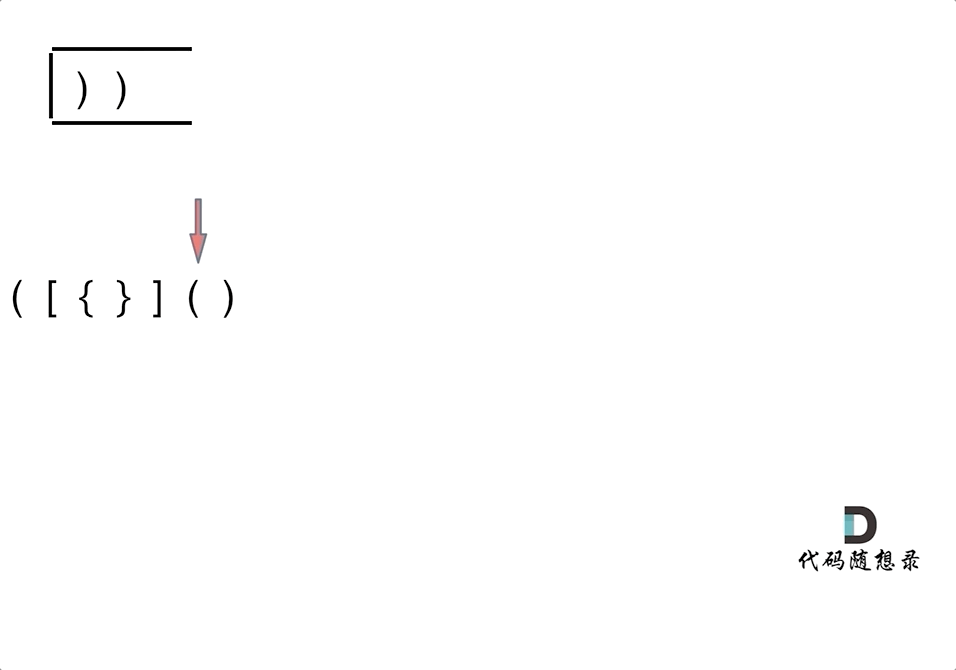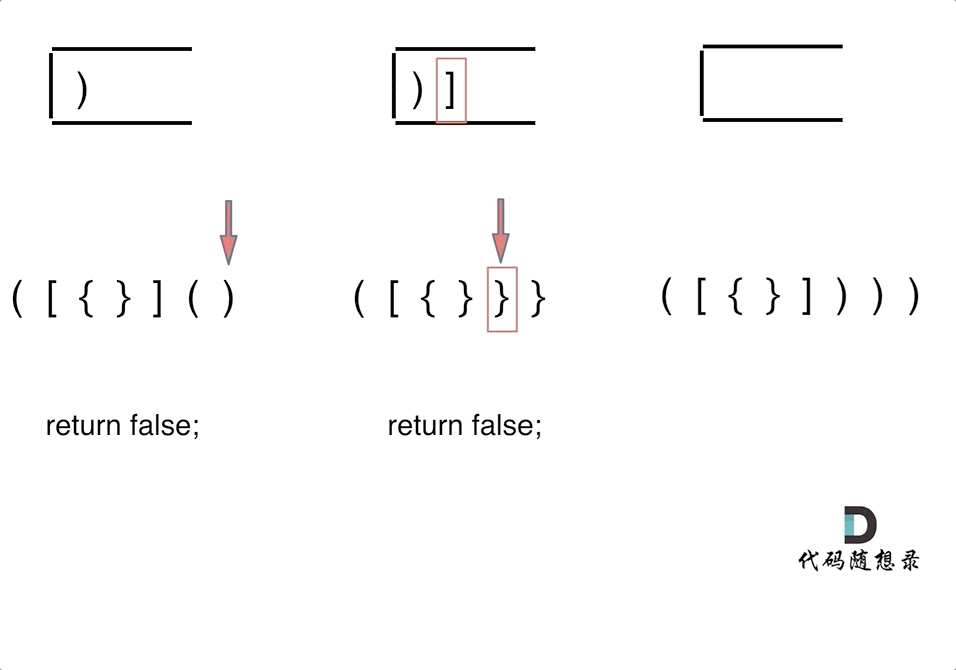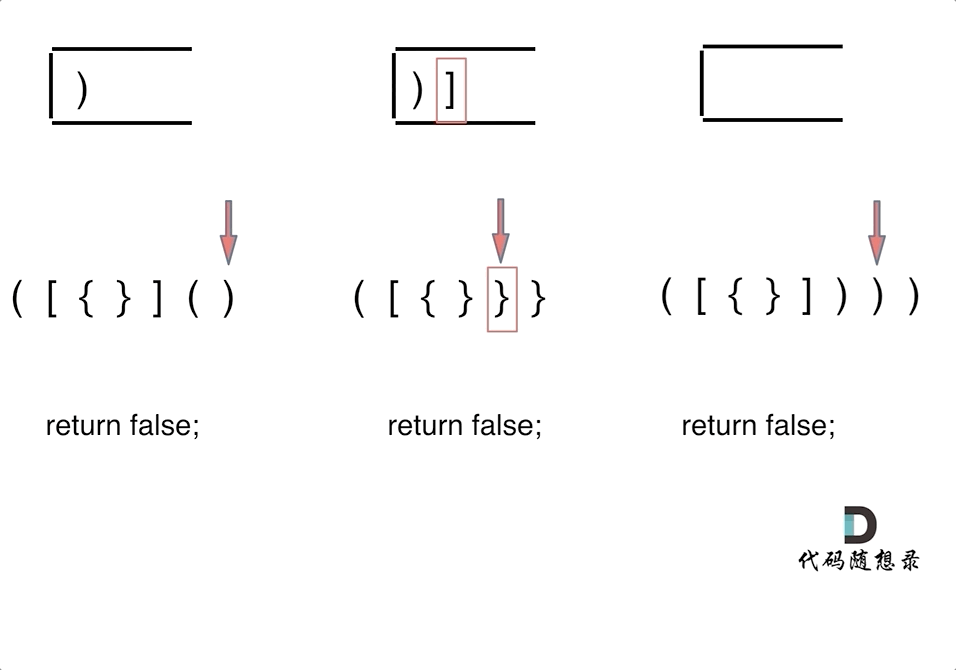
3.思路

先遍历旧栈，如果遍历的元素是左括号就在新栈中添加右括号，如果是右括号，直接看栈顶元素匹不匹配就行了，匹配就删除这个元素，最后如果新栈中的元素为空就说明全匹配成功

步骤：

第一种情况，字符串里左方向的括号多余了，所以不匹配。

（新栈的元素还没遍历完，不为空）括号匹配1

第二种情况，括号没有多余，但是括号的类型没有匹配上。
第三种情况，字符串里右方向的括号多余了，所以不匹配。

（新栈的遍历完了，但是旧栈的元素还没遍历完，还需要进行配对但是不够了）

为什么要匹配左括号时，右数组先入栈？

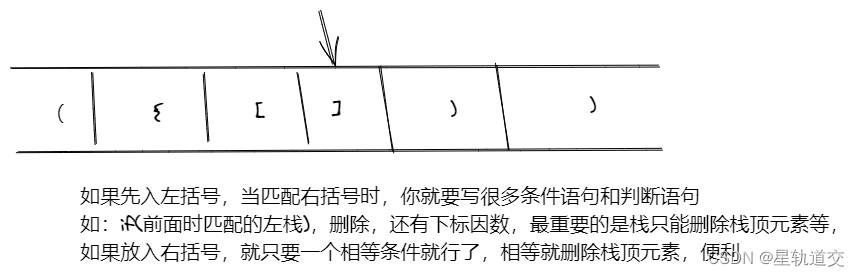
其实可以可以把左括号比作右括号

4.代码

判断奇数，只要是奇数就注定有一个括号不匹配

if (size % 2 != 0) return false;

第一种情况：当遍历完后新栈不为空，没有相应的右括号怕匹配了

return st.empty();

第二种情况：两边括号匹配不上

s[i] != st.top()

第三种情况：如果新栈为空，但是旧栈，还想匹配时

st.empty()

题目链接：1047. 删除字符串中的所有相邻重复项

匹配问题都是栈的强项

1.c++代码

class Solution {
public:
    string removeDuplicates(string s) {
   int size = s.size();
   string st;
   for (int i = 0;i < s.size(); i++) {
       if (st.back() == s[i]) {//判断是否与栈顶重复了
           st.pop_back();
       } else {
           st.push_back(s[i]);
       }
   }
   return st;
    }
};

2.思路

去除字符串中的两个相邻字符，（当三个元素相邻时会保留一个），遍历字符串，不断把字符加入新栈（这里字符串从当栈），看栈的头是否于新加入的元素匹配，匹配则删除头，否则把字符加入新栈，最后返回这个字符串。

最重要的就是把栈当成数组来使用

3白话理解

这道题目就像是我们玩过的游戏对对碰，如果相同的元素放在挨在一起就要消除。可能我们在玩游戏的时候感觉理所当然应该消除，但程序又怎么知道该如果消除呢，特别是消除之后又有新的元素可能挨在一起。此时游戏的后端逻辑就可以用一个栈来实现（我没有实际考察对对碰或者爱消除游戏的代码实现，仅从原理上进行推断）。

要知道栈为什么适合做这种类似于爱消除的操作，因为栈帮助我们记录了遍历数组当前元素时候，前一个元素是什么。

题目链接：150. 逆波兰表达式求值

一般搞不清楚顺序的一般都是栈

1.c++代码

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
     int size = tokens.size();
     stack<long long>st;
     for (int i = 0;i < size; i++) {
         if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
         long long nums1 = st.top();
         st.pop();
         long long nums2 = st.top();
         st.pop();
         if (tokens[i] == "+") {
              st.push(nums1 + nums2);
         } else if (tokens[i] == "-") {
             st.push(nums2 - nums1);
         } else if (tokens[i] == "/") {
             st.push(nums2 / nums1);
         } else if (tokens[i] == "*") {
             st.push(nums1 * nums2);
         }
         } else {
             st.push(stoll(tokens[i]));
         }
     }
     return st.top();
    }
};

2.逆波兰表达式：

是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。

该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

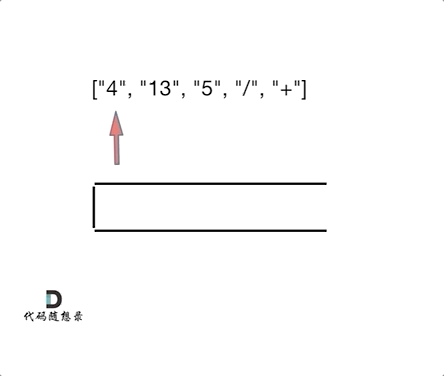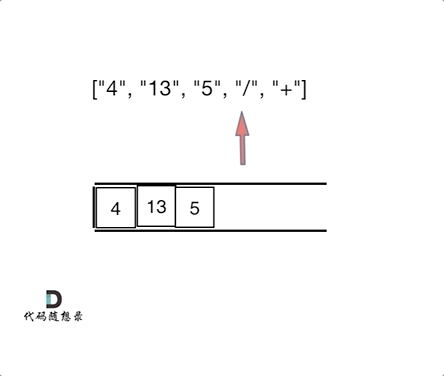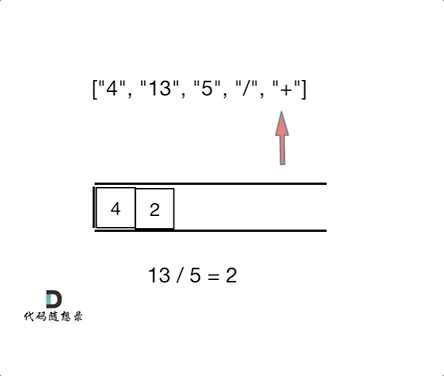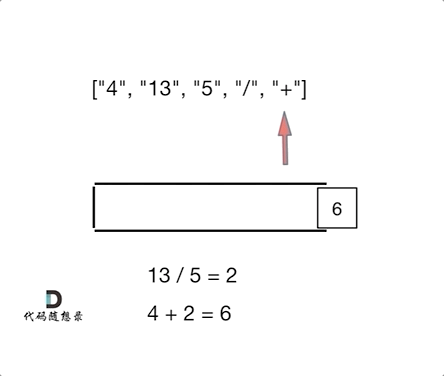
3.思路

如果遍历到这个字符是运算符，就弹出来栈中的前两个元素，把他们的运算结果加入栈，如果不是运算符，就先变成数字再加入栈中，直到算完

问题：

问题：

弹出两个元素必须先判断是不是遍历到了运算符，因为不能没个元素都弹出，会出现栈相关问题，

    if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
         long long nums1 = st.top();
         st.pop();
         long long nums2 = st.top();
         st.pop();

结果就是最后一个元素