从caffe中我们看到softmax有下面这些参数
// Message that stores parameters used by SoftmaxLayer, SoftmaxWithLossLayer
message SoftmaxParameter {
enum Engine {
DEFAULT = 0;
CAFFE = 1;
CUDNN = 2;
}
optional Engine engine = 1 [default = DEFAULT];
// The axis along which to perform the softmax -- may be negative to index
// from the end (e.g., -1 for the last axis).
// Any other axes will be evaluated as independent softmaxes.
optional int32 axis = 2 [default = 1];
}
一般来说axis也不需要修改,默认设为1,即在c上做计算。
那么设置不同的axis,结果有什么不同?我们举个例子一目了然;
import tensorflow as tf
import numpy as np
a = np.array([[1, 2, 3], [1, 2, 3]])
a = tf.cast(a, tf.float32)
#>>> a
#tf.Tensor: shape=(2, 3), dtype=float32, numpy=
#array([[1., 2., 3.],
# [1., 2., 3.]], dtype=float32)>
#
s1 = tf.nn.softmax(a,axis=0)
print(s1)
#tf.Tensor(
#[[0.5 0.5 0.5]
#[0.5 0.5 0.5]], shape=(2, 3), dtype=float32)
s2 = tf.nn.softmax(a,axis=1)
print(s2)
#tf.Tensor(
#[[0.09003057 0.24472848 0.66524094]
#[0.09003057 0.24472848 0.66524094]], shape=(2, 3), dtype=float32)
我们来看看计算过程:
axis = 0时(表示纵轴,方向从上到下)
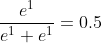
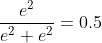
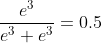
axis = 1时(表示横轴,方向从左到右)
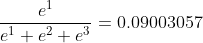
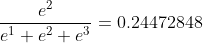
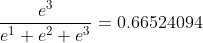
再举一个三维数组深入理解一下
import tensorflow as tf
import numpy as np
a = np.array([[[1, 2, 3], [1, 2, 3]],[[4, 5, 6], [4, 5, 6]]])
a = tf.cast(a, tf.float32)
#>>> a
#<tf.Tensor: shape=(2, 2, 3), dtype=float32, numpy=
#array([[[1., 2., 3.],
# [1., 2., 3.]],
#
# [[4., 5., 6.],
# [4., 5., 6.]]], dtype=float32)>
#
s1 = tf.nn.softmax(a,axis=0)
print(s1)
#tf.Tensor(
#[[[0.04742587 0.04742587 0.04742587]
# [0.04742587 0.04742587 0.04742587]]
#
# [[0.95257413 0.95257413 0.95257413]
# [0.95257413 0.95257413 0.95257413]]], shape=(2, 2, 3), dtype=float32)
s2 = tf.nn.softmax(a,axis=1)
print(s2)
#tf.Tensor(
#[[[0.5 0.5 0.5]
# [0.5 0.5 0.5]]
#
# [[0.5 0.5 0.5]
# [0.5 0.5 0.5]]], shape=(2, 2, 3), dtype=float32)
s3 = tf.nn.softmax(a,axis=2)
print(s3)
#tf.Tensor(
#[[[0.09003057 0.24472848 0.66524094]
# [0.09003057 0.24472848 0.66524094]]
#
# [[0.09003057 0.24472848 0.66524094]
# [0.09003057 0.24472848 0.66524094]]], shape=(2, 2, 3), dtype=float32)
计算过程如下:
axis=0时
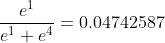
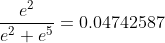
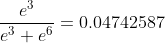
。。。再来重复上面3个计算3次
axis=1时(1和2的计算和上面二维差不多)
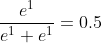
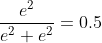
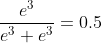
。。。
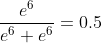
axis=2时
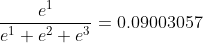
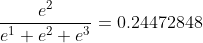
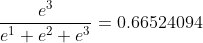
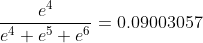
…
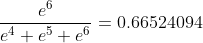





 本文通过实例详细解析了在TensorFlow中使用Softmax函数时,轴参数(axis)的不同设置如何影响计算结果,对比了在二维和三维数组上的具体差异。
本文通过实例详细解析了在TensorFlow中使用Softmax函数时,轴参数(axis)的不同设置如何影响计算结果,对比了在二维和三维数组上的具体差异。
















 7268
7268

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








