poj 2054（贪心）

   可能真是智商压制，开始拿到题想了一整天，一点思路也没有， 然后看别人的博客也感觉半知半解，但自己写完的时候，发现这题确实挺好的，挺锻炼思维的，建议大家多思考思考。

    大牛的思路：（自己写的代码，将就看下吧，最好是边看代码，边看题解）

贪心原则应该是Ci大的尽量先染色，但是由于父节点染了才能染子节点的限制使得问题不好解决了，但是Ci大的一定是在其父节点染色后立即被染色，这时大牛们的思路我也没有看明白如何证明的，但仔细一想就明白了。于是我们根据这个条件就可以将Ci大的点与其父节点合并在一起组成一个集合。这样就可以将问题规模减小。

   合并后的点（即集合）的属性如何变化呢？假如设fact[i]表示集合的Ci和，iNum[i]表示i所属集合的结点个数；那么把fact[i]/iNum[i]作为贪心原则，其值大者先合并到其父节点，最终合并成一个集合。答案是怎么得出来的我看了很长时间才明白。先看一下下面的例子;

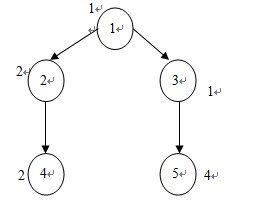
先初始化fact[i]=Ci, iNum[i]=1;将每一个点看成一个集合。

按照贪心原则首先选择5合并到3形成集合A={3,5}，fact[A]=5,iNum[A]=2;

Ans+=fact[5]*iNum[3]=4；

然后再按照贪心原则选择集合A合并到1形成集合B={1,3,5}，fact[B]=6,iNum[B]=3;

Ans+=fact[A]*iNum[1]=9;

然后再选择2合并到集合B形成集合C={1,2,3,5}，fact[C]=8, iNum[C]=4;

Ans+=fact[2]*iNum[B]=15;

最后选择4合并到集合C形成集合D={1,2,3,4,5}，fact[D]=10,iNum[D]=5;

Ans+=fact[4]*iNum[C]=23;

最后别忘了Ans+=fact[D]=33;

#include<cstdio>
#include<iostream>
#include<cstring>
#define N 1010
using namespace std;
int fa[N];
int a[N];
int num[N];
bool vis[N];
int n, root;
int fint()
{
  int k;
  double ma = 0;
  for(int i=1; i<=n; ++i)
   if(i!=root&&vis[i]&&ma < a[i]*1.0/num[i])
   {
     ma = a[i]*1.0/num[i];
     k = i;
   }
   return k;
}
int main()
{
 while(cin >> n >> root, n||root)
 {
  memset(vis,true,sizeof(vis));
  memset(fa,0,sizeof(fa));
  for(int i=1; i<=n; ++i)
  num[i] = 1;
  for(int i=1; i<=n; ++i)
    cin >> a[i];
  int x,y;
  for(int i=1; i<n; ++i)
  {
   cin >> x >> y;
   fa[y] = x;
  }
  int ans = 0,k,g;
  for(int i=1; i<n; ++i)
  {
   k = fint();
   vis[k] = false;
   g = fa[k];
   while(!vis[g]) g = fa[g];
   ans += (num[g]*a[k]);
   num[g] += num[k];
   a[g] += a[k];
   for(int e=1; e<=n; ++e)
   if(fa[e] == k)
   {
     fa[e] =  g;
   }
  }
  ans += a[root];
  cout << ans <<endl;
 }
 return 0;
}