杭电ACM 1022 Train Problem I

Problem Description

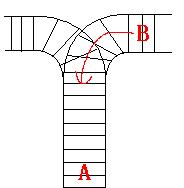
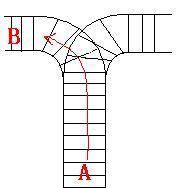
As the new term comes, the Ignatius Train Station is very busy nowadays. A lot of student want to get back to school by train(because the trains in the Ignatius Train Station is the fastest all over the world ^v^). But here comes a problem, there is only one railway where all the trains stop. So all the trains come in from one side and get out from the other side. For this problem, if train A gets into the railway first, and then train B gets into the railway before train A leaves, train A can't leave until train B leaves. The pictures below figure out the problem. Now the problem for you is, there are at most 9 trains in the station, all the trains has an ID(numbered from 1 to n), the trains get into the railway in an order O1, your task is to determine whether the trains can get out in an order O2.

 

Input

The input contains several test cases. Each test case consists of an integer, the number of trains, and two strings, the order of the trains come in:O1, and the order of the trains leave:O2. The input is terminated by the end of file. More details in the Sample Input.

 

Output

The output contains a string "No." if you can't exchange O2 to O1, or you should output a line contains "Yes.", and then output your way in exchanging the order(you should output "in" for a train getting into the railway, and "out" for a train getting out of the railway). Print a line contains "FINISH" after each test case. More details in the Sample Output.

 

Sample Input

3 123 321
3 123 312

 

Sample Output

Yes.
in
in
in
out
out
out
FINISH
No.
FINISH

Hint
Hint
 
For the first Sample Input, we let train 1 get in, then train 2 and train 3.
So now train 3 is at the top of the railway, so train 3 can leave first, then train 2 and train 1.
In the second Sample input, we should let train 3 leave first, so we have to let train 1 get in, then train 2 and train 3.
Now we can let train 3 leave.
But after that we can't let train 1 leave before train 2, because train 2 is at the top of the railway at the moment.
So we output "No.".

//代码非常简洁
#include<cstdio>
int main()
{
    char in[12],out[12],stack[20];
    int n,i,j,k,top,flag[20];		//flag设置的非常好！进栈就赋值1，出栈就是0，
									//最后输出in或者out只需要看flag数组的值就好了
    while(scanf("%d %s %s",&n,in,out)!=EOF)	//看这读取，多么干脆利落！
    {
        top=-1;
        i=j=k=0;
        while(i<n&&j<n+1)           //进栈时j++，出栈时i++,先进栈后出栈，进栈完毕后不能结束，故j<n+1 
        {                        
            if(out[i]==stack[top]&&top!=-1)	//拿stack和out比对，对上号就出栈
            {
                i++,top--;              
                flag[k++]=0;          
            }
            else						//拿stack和out比对，对不上号就没法出栈，就进栈
            {
                stack[++top]=in[j];
                j++;
                flag[k++]=1;           
            }      
        }  
        if(k==2*n)		//等于所有火车的二倍，说明进栈出栈次数相等
        {
            printf("Yes.\n");
            for(i=0; i<k; i++)
            {
                if(flag[i])
                    printf("in\n");
                else 
                    printf("out\n");
            }
        }
        else
        {
            printf("No.\n");
        }
         printf("FINISH\n");
    }
    return 0;
}