Chapter 3: 大语言模型基础 Part 3：Transformer 的心脏—

上一篇我们实现了 Transformer 的 Encoder-Decoder 骨架代码。本篇将填充其中最关键的模块：MultiHeadAttention，并深入解析 Q、K、V 的运作原理。

3.1.2 Transformer 架构解析 (续)

(2) 从自注意力到多头注意力

现在，我们来填充骨架中最关键的模块：注意力机制。

自注意力 (Self-Attention) 的直观理解

想象一下我们阅读这个句子：“The agent learns because it is intelligent.”。

当我们读到加粗的 “it” 时，为了理解它的指代，我们的大脑会不自觉地将更多的注意力放在前面的 “agent” 这个词上。自注意力 (Self-Attention) 机制就是对这种现象的数学建模。

它允许模型在处理序列中的每一个词时，都能兼顾句子中的所有其他词，并为这些词分配不同的“注意力权重”。权重越高的词，代表其与当前词的关联性越强。

核心概念：Q、K、V

为了实现上述过程，自注意力机制为每个输入的词元向量引入了三个可学习的角色：

查询 (Query, Q)：代表当前词元，它正在主动地“查询”其他词元以获取信息。
键 (Key, K)：代表句子中可被查询的词元“标签”或“索引”。
值 (Value, V)：代表词元本身所携带的“内容”或“信息”。

💡 深度解析：

这三个向量都是由原始的词嵌入向量乘以三个不同的、可学习的权重矩阵 ( $W^Q, W^K, W^V$ ) 得到的。你可以把它想象成一次高效的开卷考试：

Q (Query)：你手中的考题。

K (Key)：教科书中每一章的标题。

V (Value)：教科书中每一章的具体内容。

你拿着考题 (Q)，去和每一章的标题 (K) 匹配。匹配度越高，你就越需要仔细阅读那一章的内容 (V)。

计算过程：一步步拆解

整个计算过程可以分为以下几步：

准备“考题”和“资料”：对于句子中的每个词，生成其 Q, K, V 向量。
计算相关性得分：用词 A 的 Q 向量，去和句子中所有词（包括 A 自己）的 K 向量进行点积运算。得分越高，相关性越强。
稳定化与归一化：将分数除以一个缩放因子 $dk\sqrt{d_k}$ （ $d_k$ 是 K 向量的维度），防止梯度消失/爆炸。然后用 Softmax 函数将分数转换成总和为 1 的概率分布（即注意力权重）。
加权求和：将权重分别乘以每个词对应的 V 向量，然后将所有结果相加。

这个过程可以用一个简洁的公式来概括：

$Attention(Q,K,V)=softmax(QKTdk)VAttention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V$

多头注意力 (Multi-Head Attention)

如果只进行一次上述的注意力计算（即单头），模型可能会只学会关注一种类型的关联（比如只关注语法上的主谓关系）。但语言是复杂的，我们需要模型能同时关注多种关系（如指代关系、时态关系等）。

多头注意力应运而生。它的思想很简单：把一次做完变成分成几组，分开做，再合并 。

它将原始的 Q, K, V 向量在维度上切分成 $h$ 份（ $h$ 就是“头”数），每一份都独立地进行一次单头注意力的计算。这就好比让 $h$ 个不同的“专家”从不同的角度去审视句子。最后，将这些专家的“意见”（即输出向量）拼接起来，再通过一个线性变换进行整合。
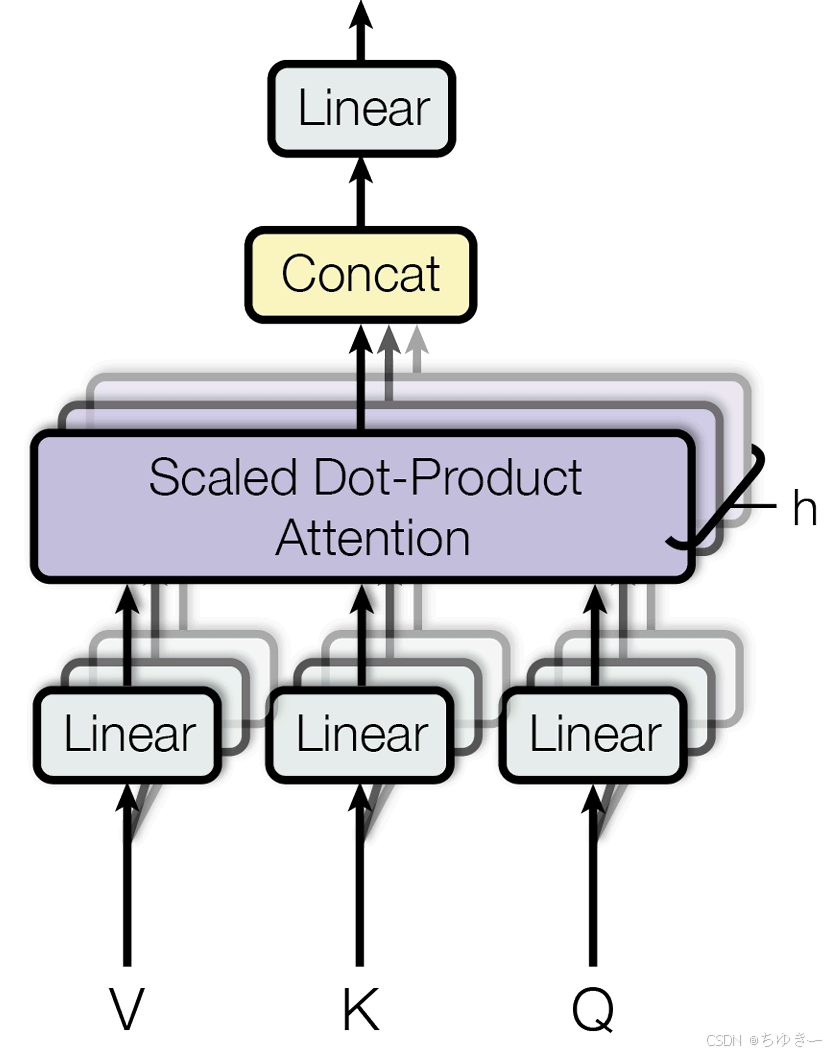
在这里插入图片描述

代码实现：MultiHeadAttention

以下是多头注意力机制的完整 PyTorch 实现。这段代码实现了从分头、计算缩放点积注意力，到合并输出的全过程。

import torch
import torch.nn as nn
import math

class MultiHeadAttention(nn.Module):
    """多头注意力机制模块"""
    
    def __init__(self, d_model, num_heads):
        super(MultiHeadAttention, self).__init__()
        
        assert d_model % num_heads == 0, "d_model 必须能被 num_heads 整除"
        
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_k = d_model // num_heads  # 每个头的维度
        
        # 定义 Q, K, V 和输出的线性变换层
        self.w_q = nn.Linear(d_model, d_model)
        self.w_k = nn.Linear(d_model, d_model)
        self.w_v = nn.Linear(d_model, d_model)
        self.w_o = nn.Linear(d_model, d_model)

    def scaled_dot_product_attention(self, Q, K, V, mask=None):
        """计算缩放点积注意力"""
        # 1. 计算注意力得分 (QK^T / sqrt(d_k))
        # K.transpose(-2, -1) 是为了将最后两个维度转置，以便进行矩阵乘法
        attn_scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
        
        # 2. 应用掩码 (如果提供)
        if mask is not None:
            # 将掩码中为 0 的位置设置为一个非常小的负数，这样 softmax 后会接近 0
            attn_scores = attn_scores.masked_fill(mask == 0, -1e9)
            
        # 3. 计算注意力权重 (Softmax)
        attn_probs = torch.softmax(attn_scores, dim=-1)
        
        # 4. 加权求和 (权重 * V)
        output = torch.matmul(attn_probs, V)
        
        return output

    def split_heads(self, x):
        """
        将输入的形状从 (batch_size, seq_length, d_model) 
        变换为 (batch_size, num_heads, seq_length, d_k)
        然后转置为 (batch_size, num_heads, seq_length, d_k) 以便并行计算
        """
        batch_size, seq_length, d_model = x.size()
        return x.view(batch_size, seq_length, self.num_heads, self.d_k).transpose(1, 2)

    def combine_heads(self, x):
        """
        将输入的形状从 (batch_size, num_heads, seq_length, d_k)
        变回 (batch_size, seq_length, d_model)
        """
        batch_size, num_heads, seq_length, d_k = x.size()
        return x.transpose(1, 2).contiguous().view(batch_size, seq_length, self.d_model)

    def forward(self, Q, K, V, mask=None):
        # 1. 对 Q, K, V 进行线性变换，并切分成多头
        # 注意：这里传入的 Q, K, V 通常是同一个 x (自注意力)，或者是 decoder_x 和 encoder_out (交叉注意力)
        Q = self.split_heads(self.w_q(Q))
        K = self.split_heads(self.w_k(K))
        V = self.split_heads(self.w_v(V))
        
        # 2. 计算缩放点积注意力 (这一步是并行计算所有头的)
        attn_output = self.scaled_dot_product_attention(Q, K, V, mask)
        
        # 3. 合并多头输出并进行最终的线性变换
        output = self.w_o(self.combine_heads(attn_output))
        
        return output

💡 注解：

在实际工程中，split_heads 和 combine_heads 的操作使用了 view 和 transpose。这里的 transpose(1, 2) 是关键，它将 num_heads 维度移到了序列长度之前，使得 PyTorch 能够利用广播机制一次性并行计算所有头的注意力得分，这是 Transformer 训练速度快的秘诀之一。