计算机视觉中的图像滤波

对下图进行滤波处理（均值滤波、中值滤波）

1.基本思想

（1）均值滤波：任意一点的像素值，是周围n*n个像素值的均值

①选择适当的卷积核n*n，比如3*3，5*5，7*7，与原图像卷积；

②得到的结果除以n*n，代替中间的像素的灰度值；

③滑动卷积核，重复第②步，直到遍历图像结束。

（2）中值滤波：任意一点的像素值，是周围n*n个像素值的中间值

①选择适当的卷积核n*n，比如3*3，5*5，7*7

②按灰度值升或降序排列，取位于中间的灰度值来代替中间点的灰度值

③滑动卷积核，重复第②步，直到遍历图像结束。

2.代码实现（matlab）

（1）均值滤波

img = imread('face.png');

n = 7;  %卷积核尺寸

kernel = 1 / (n * n) .* ones(n, n); %n*n的核

[h, w] = size(img);    %图片尺寸

x1 = double(img);

x = x1;

%均值滤波

for i = 1:h-n+1

    for j = 1:w-n+1

        ave = sum( sum( x(i:i+n-1,j:j+n-1) .* kernel)); %卷积核与图像卷积

        x(i+(n-1)/2,j+(n-1)/2) = ave;

    end

end

g = uint8(x);

subplot(1 ,2, 1);

imshow(img)

subplot(1 ,2, 2);

imshow(g);

（2）中值滤波

img = imread('face.png');

n = 7;      %卷积核尺寸

[h, w] = size(img);     %图片尺寸

x1 = double(img);   %转double为了矩阵运算

x = x1;

%中值滤波

for i = 1:h-n+1

    for j = 1:w-n+1

        c = x1(i:i+n-1,j:j+n-1);

        a = [ ];

        for k = 1:n

            a = [a, c(k, :)];%把矩阵转变成一个一维向量

        end

        tmp = median(a);

        x(i+(n-1)/2,j+(n-1)/2) = tmp;

    end

end

g = uint8(x);      %取整，转int8

subplot(1 ,2, 1);

title('原图像')

imshow(img)

subplot(1 ,2, 2);

imshow(g);

3.运行结果

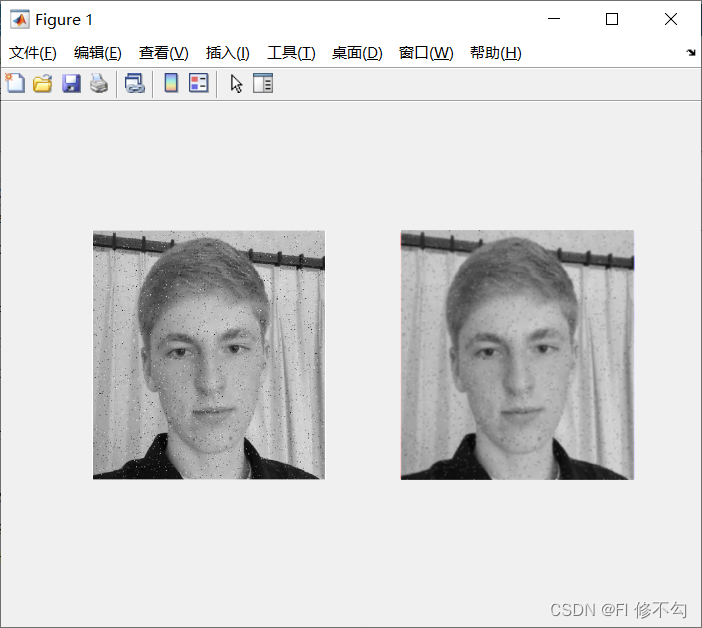
均值滤波对比

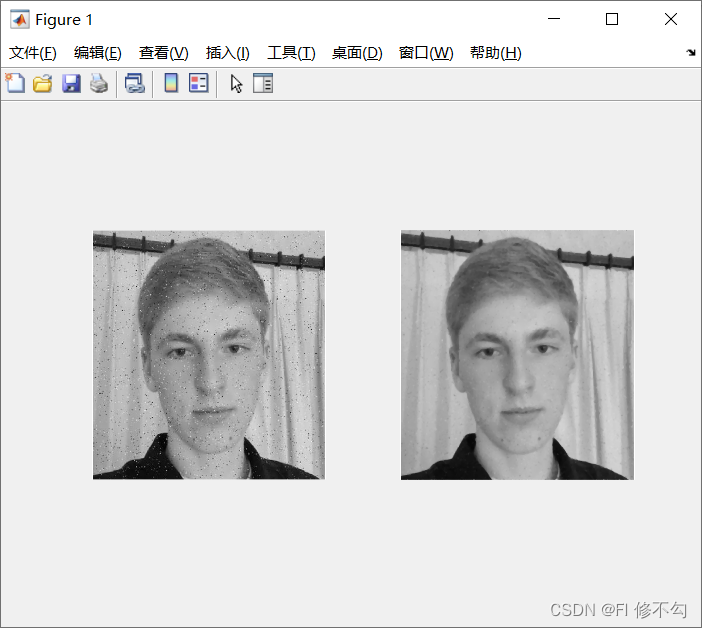
中值滤波对比

调用OpenCv中的blur和medianBlur函数实现滤波功能

import cv2

img = cv2.imread(r"C:/Users/pc/Desktop/face.png",0)

cv2.imshow('img',img)

#均值滤波

new_img1 = cv2.blur(img,(7,7))

cv2.imshow('new_img1',new_img1)

#中值滤波

new_img2 = cv2.medianBlur(img,7)

cv2.imshow('new_img2',new_img2)

                 原灰度图
结果如下

               

                       中值滤波

                       均值滤波

4.思考和总结

       滤波使图像变得平滑，噪声得以去除，均值滤波使图像变得更加模糊，中值滤波是非线性滤波，能更好的处理椒盐噪声，此外，适当地选取卷积核的大小可以有效地改善滤波的效果。