牛客网在线编程专题《剑指offer-面试题36》数组中的逆序对

最新推荐文章于 2020-01-10 21:18:02 发布

原创最新推荐文章于 2020-01-10 21:18:02 发布 · 560 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#剑指offer #数组 #逆序对

算法同时被 2 个专栏收录

82 篇文章

订阅专栏

剑指offer

46 篇文章

订阅专栏

本文探讨了逆序对的两种求解方法：暴力解法和归并排序思想的运用。首先介绍了简单但效率低下的两层循环遍历法，然后深入解析了归并排序如何有效降低时间复杂度。通过Java和Python代码实例，展示了如何利用归并排序核心思想解决逆序对问题。

题目链接：

https://www.nowcoder.com/practice/96bd6684e04a44eb80e6a68efc0ec6c5?tpId=13&tqId=11188&tPage=2&rp=2&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

题目描述：

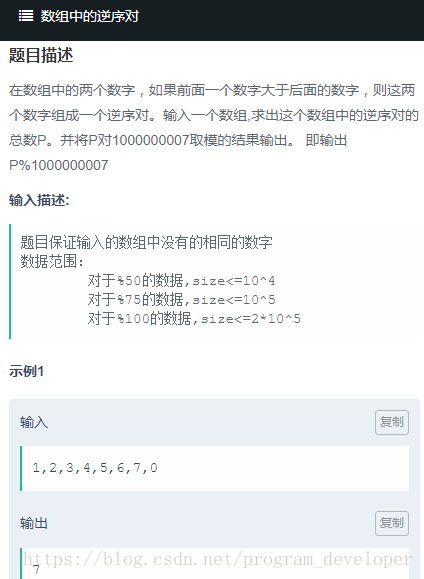
解题思路：

（1）两层循环遍历，时间复杂度为O( $n^{2}$ )。

顺序扫描整个数组，每扫描到一个数字的时候，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成一个逆序对。假设数组中含有n个数字，由于每个数字都要和O(n)个数字作比较，因此这个算法的时间复杂度是O( $n^{2}$ )。

代码实现：

public class Solution {
    public int InversePairs(int [] array) {
        int count = 0;
        for(int i=0; i<array.length; i++) {
        	for(int j=i; j<array.length; j++) {
        		if(array[i] > array[j])
        			count++;
        	}
        }
        return count;
    }
}

结果：不能被AC。

（2）归并排序的思想实现：

已经AC的代码：

public class ArrayInversePairs {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] arr = {7, 5, 6, 4};
		System.out.println(InversePairs(arr));
	}

    public static int InversePairs(int[] array) {
    	
    	if(array == null || array.length <= 0) {
    		return 0;
    	}
    	
    	int[] tmpArr = new int[array.length];
    	for(int i = 0; i < array.length; i++) {
    		tmpArr[i] = array[i];
    	}
    	int count = InversePairsCore(array, tmpArr, 0, array.length - 1);
    	return count;
    }  
    
    public static int InversePairsCore(int[] arr, int[] tmpArr, int low, int high) {
    	if(low == high) {
    		tmpArr[low] = arr[low];
    		return 0;
    	}
    	int len = (high - low) / 2;
    	int left = InversePairsCore(tmpArr, arr, low, low + len) % 1000000007;
    	int right = InversePairsCore(tmpArr, arr, low + len + 1, high) % 1000000007;
    	//p1初始化为前半段最后一个数字的下标
    	int p1 = low + len;
    	//p2 初始化为后半段最后一个数字的下标
    	int p2 = high;
    	// 开始拷贝的位置
    	int p3 = high;
    	// 逆序数
    	int count = 0;
    	while(p1 >= low && p2 >= low + len + 1) {
    		if(arr[p1] > arr[p2]) {
    			//对应的逆序数
    			count += p2 - low - len;
    			tmpArr[p3] = arr[p1];
    			p3--;
    			p1--;
    			if(count >= 1000000007)
    				count %= 1000000007;
    		} else {
    			tmpArr[p3] = arr[p2];
    			p3--;
    			p2--;
    		}
    	}
    	
    	while(p1 >= low) {
    		tmpArr[p3] = arr[p1];
    		p3--;
    		p1--;
    	}
    	
    	while(p2 >= low + len + 1) {
    		tmpArr[p3] = arr[p2];
    		p3--;
    		p2--;
    	}
    	
    	return (count + left + right) % 1000000007;
    }
    
}

（3）用Python实现归并排序的思想

归并排序能够有效的减少最坏时间复杂度，但是它有额外的开销，以空间换时间。归并排序，就是把原数据分成两个数组，每次取两个数组中的最小值放入一个新的数组中，直到其中一个数组全部取完。归并排序思想没法用python做，用python始终是超时的。

class Solution:

    def InversePairs(self, data):
        if data is None or len(data) <= 0:
            return 0

        copy = [i for i in data]

        count = self.InversePairsCore(data, copy, 0, len(data) - 1)

        return count % 1000000007

    def InversePairsCore(self, data, copy, start, end):
        if start == end:
            copy[start] = data[start]
            return 0

        length = (end - start) // 2
        left = self.InversePairsCore(copy, data, start, start + length)
        right = self.InversePairsCore(copy, data, start + length + 1, end)

        # p1 初始化为前半段最后一个数字的下标
        p1 = start + length
        # p2 初始化为后半段最后一个数字的下标
        p2 = end
        # 开始拷贝的位置
        p3 = end
        # 逆序数
        count = 0

        # 对两个数组进行对比取值的过程
        while p1 >= start and p2 >= start + length + 1:
            if data[p1] > data[p2]:
                copy[p3] = data[p1]
                p3 -= 1
                p1 -= 1
                # 对应的逆序数
                count += p2 - start - length
            else:
                copy[p3] = data[p2]
                p3 -= 1
                p2 -= 1

        # 剩下的一个数组未取完的操作
        while p1 >= start:
            copy[p3] = data[p1]
            p3 -= 1
            p1 -= 1

        while p2 >= start + length + 1:
            copy[p3] = data[p2]
            p3 -= 1
            p2 -= 1

        return count + left + right


if __name__ == "__main__":
    # input_data = [7, 5, 6, 4]
    input_data = [1, 2, 3, 4, 5, 6, 7, 0]
    sol = Solution()
    print(sol.InversePairs(input_data))