动态规划学习-【国王和金矿】

微信公众号

题目：

有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半金矿。要求用程序求解出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？

方法一：排列组合

每一座金矿都有挖与不挖两种选择，如果有N座金矿，排列组合起来就有2^N种选择。对所有可能性做遍历，排除那些使用工人数超过10的选择，在剩下的选择里找出获得金币数最多的选择。

代码比较简单就不展示了，时间复杂度也很明显，就是O(2^N)。

对问题的详细分析：

动态规划有三个核心元素：最优子结构、边界、状态转移方程式。

问题的最优子结构：一个是4金矿10工人时的最优选择，一个是4金矿（10-3）工人时的最优选择。

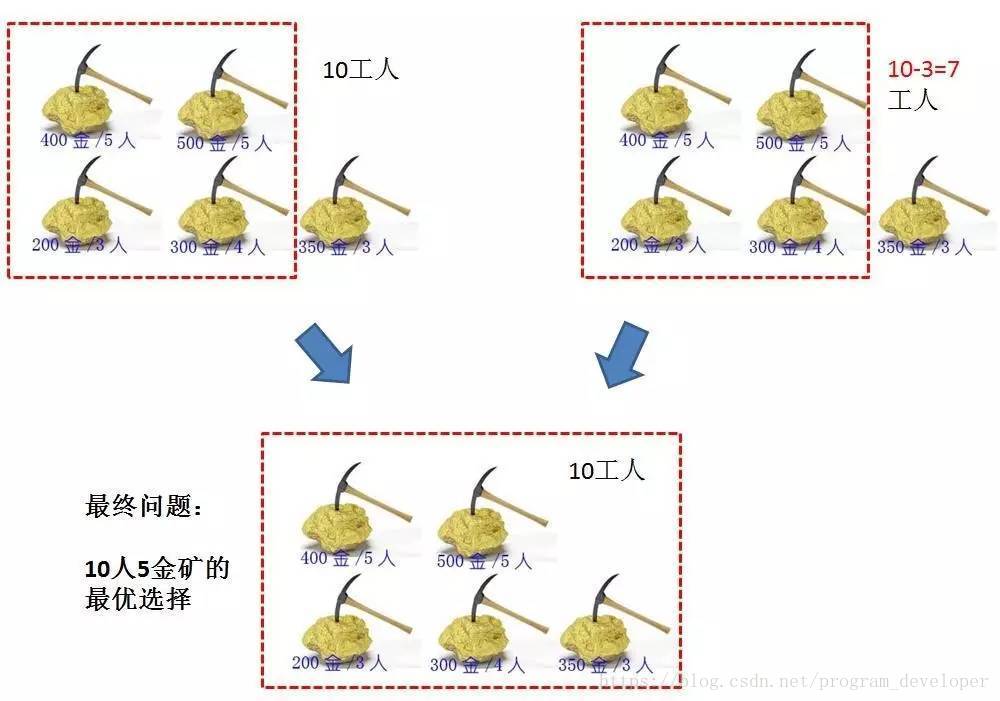
 我们来分析一下最优子结构和最终问题的关系。换句话说，4个金矿的最优选择和5个金矿的最优选择之间，是什么样的关系？

5个金矿的最优选择，就是（前4座金矿10工人的挖金数量）和（前4座金矿7工人的挖金数量+第5座金矿的挖金数量）的最大值。

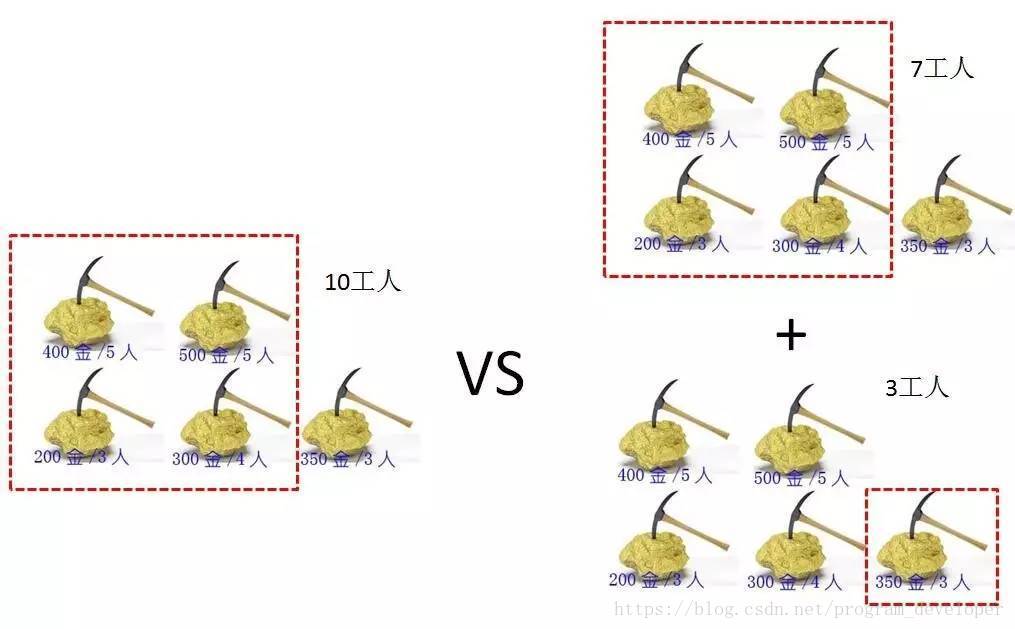
 下面，我们把金矿数量设为N，工人数设为W，金矿的黄金量设为数组G[]，金矿的用工量设为数组P[]。

那么5座金矿和4座金矿的最优选择之间存在这样的关系：F(5,10) = MAX( F(4,10), F(4,10-P[4])+G[4] ) 注意：数组下标从0开始。

最后我们还需要确定一下，这个问题的边界是什么？

边界两种情况：（1）只有1座金矿，也就是N=1的时候。这时候没得选，只能挖这座唯一的金矿，得到的黄金数量就是G[0]。（2）如果给定的工人数量不够挖取第1座金矿，也就是 W < P[0] 的时候，那么得到的黄金数就是0了。

用公式来表达如下：

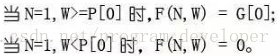
经过上面的分析，我们可以得出这个问题完整的状态转移方程：

F (N,W) = 0 （当N <= 1, W < P[0]）;

F (N,W) = G[0] （当N == 1, W >= P[0]）;

F (N,W) = F(N-1, W) （当N > 1, W < P[N - 1]）;<